第23章 旋转复习小结 第1课时 知识要点-2024-2025学年九年级数学上册教材配套同步课件（人教版）

这是一份第23章 旋转复习小结 第1课时 知识要点-2024-2025学年九年级数学上册教材配套同步课件（人教版），共27页。

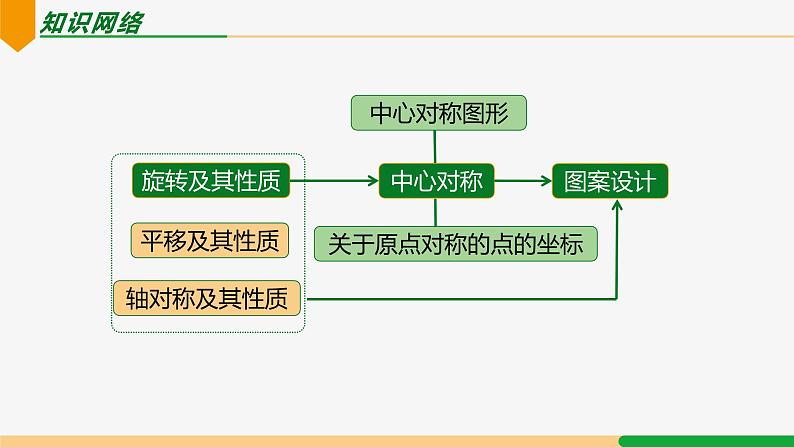
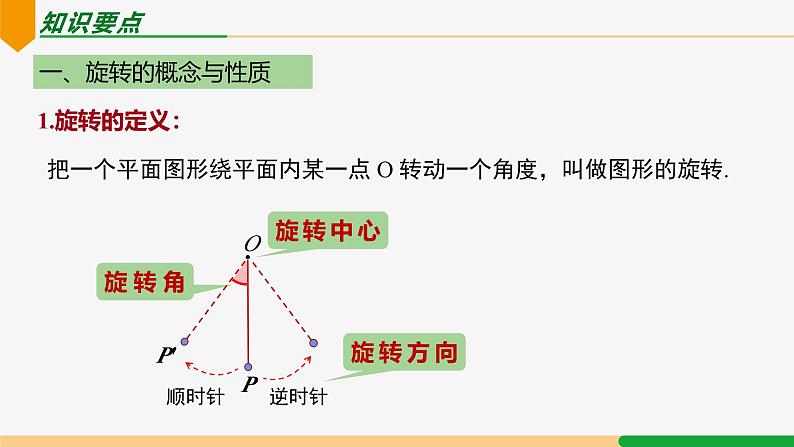
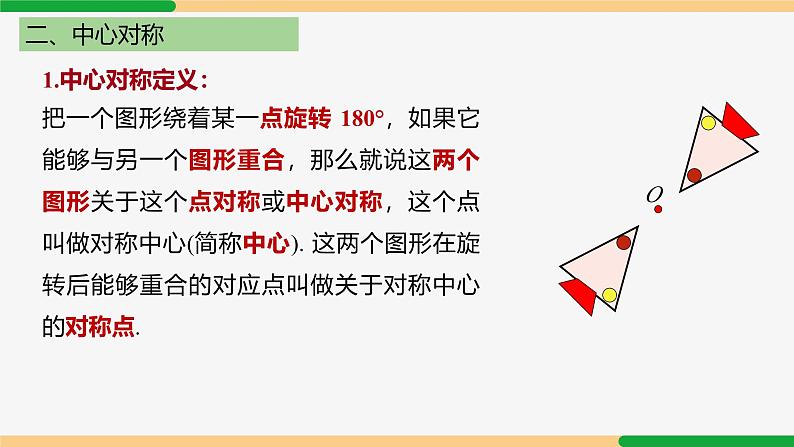
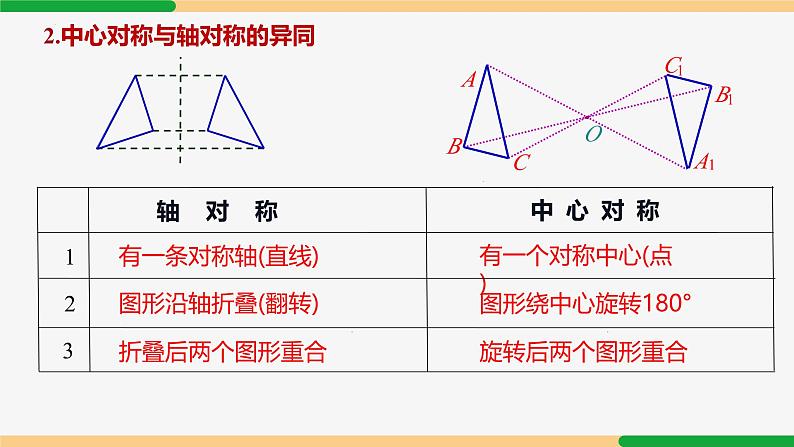
知识要点第23章 旋转复习和小结| 第1课时|知识网络旋转及其性质平移及其性质轴对称及其性质中心对称图形中心对称关于原点对称的点的坐标图案设计知识要点一、旋转的概念与性质1.旋转的定义：把一个平面图形绕平面内某一点 O 转动一个角度，叫做图形的旋转.顺时针旋转中心旋转角旋转方向逆时针P′P2.旋转的性质：2. 对应点与旋转中心所连线段的夹角等于旋转角；1. 对应点到旋转中心的距离相等；3. 旋转前、后的图形全等.3.旋转的作图步骤：连中心、转角度、取相等、画图形 二、中心对称O1.中心对称定义：把一个图形绕着某一点旋转 180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心(简称中心). 这两个图形在旋转后能够重合的对应点叫做关于对称中心的对称点. 轴 对 称中心对称1有一条对称轴(直线)有一个对称中心(点)2图形沿轴折叠(翻转) 图形绕中心旋转180°3折叠后两个图形重合旋转后两个图形重合12.中心对称与轴对称的异同3.中心对称的性质：1. 中心对称的两个图形是全等图形.2. 中心对称的两个图形，对称点所连线段都经过对称中心，并且被对称中心所平分(即每组对称点与对称中心三点共线)；4.中心对称的作图：连中心、顺延长、取相等、画图形5.中心对称图形的定义：把一个图形绕某一个点旋转 180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心 6.常见对称图形：三、关于原点对称的点的坐标Ox1.关于原点对称的点的坐标为 P′(－a，－b).2.关于 x 轴对称的点的坐标为 P′(a，－b)，3. 关于 y 轴对称的点的坐标为 P′(－a， b).简记为：关于谁，谁不变，关于原点都改变”.点 P(a，b)考点讲解例1 如图，△ABO 经顺时针旋转后能与△CDO 重合，则： (1) 旋转中心是 ，旋转角度是 °； (2) 线段 BO 的对应线段是 ， 线段 AB 的对应线段是 ； (3)∠AOB 的对应角是 ， ∠ABO 的对应角是 .点 O 90 DO CD ∠COD ∠CDO 考点一 旋转的概念例2 (1)如图 a，将△AOB 绕点 O 按逆时针方向旋转 60°后得到△COD，若∠AOB = 15°，则∠AOD 的度数是 ( ) A. 15° B. 60° C. 45° D. 75°C考点二 旋转的性质(2) 如图 b，4×4 的正方形网格中，△MNP 绕某点旋转一定的角度，得到△M1N1P1，其旋转中心是( )A. 点 A B. 点 B C. 点 C D. 点 DB例3 如图，在边长为 1 的正方形组成的网格中，每个正方形的顶点称为格点.已知△AOB 的顶点均在格点上，建立如图所示的平面直角坐标系，点 A、B 的坐标分别是 A(3，2) 、B(1，3). (1) 将△AOB 绕点 O 逆时针旋转 90°后得到△A1OB1，画出旋转后的图形； (2) 画出△AOB 关于原点 O 对称的图形△A2OB2，并写出点 A2，B2 的坐标.考点三 旋转的作图考点四 中心对称例4下列图形中，既是轴对称图形，又是中心对称图形的是(　　)　　A　　　　　 B　　　　　 C 　　　　 DD例5 如图，从前一个农民有一块平行四边形的土地，地里有一个圆形池塘.农民立下遗嘱：要把这块土地平分给他的两个儿子，中间池塘也同时平分.农民的两个儿子不知怎么做，你能想个办法吗？A例6 若点 A (2m－1，2n + 3) 与 B (2－m，2－n) 关于原点 O 对称，则 m =_____， n =_____．－1－5解：点 A 与 B 关于原点 O 对称2m－1 + 2－m = 02n + 3 + 2－n = 0课堂练习1. 如图，在 4×4 的正方形网格中，每个小正方形的边长均为 1，将三角形 AOB 绕点 O 逆时针旋转 90° 得到三角形 COD，则旋转过程中形成的阴影部分的面积为_______．2.如图，在△ABC 中，∠ACB＝90°，∠BAC＝α，将△ABC 绕点 C 顺时针旋转 90° 得到△A′B′C ，点 B 的对应点 B′ 在边 AC上 (不与点 A，C 重合)，则∠AA′B′ 的度数为( ) A．α B．α－45° C．45°－α D．90°－α C 3. 如图，在正方形网格中，△ABC 的顶点都在格点(小正方形的顶点)上，将△ABC 绕点 A 按逆时针方向旋转 90° 得到△AB1C1. 请你作出△AB1C1.4. 如图，在 Rt△ABC 中，∠ACB = 90°，点 D，E 分别在 AB，AC 上，CE = BC，连接 CD，将线段 CD 绕点 C 按顺时针方向旋转 90° 后得 CF，连接 EF．(1) 补充完成图形；(2) 若 EF∥CD，求证：∠BDC = 90°．解：(1) 补全图形，如图所示.(2) 由旋转的性质，得 DC = FC，∠DCF = 90°，∴∠DCE +∠ECF = 90°.∵∠ACB = 90°，∴∠DCE +∠BCD = 90°. ∴∠ECF =∠BCD.∴△BDC≌△EFC (SAS). ∴∠BDC =∠EFC.∵ EF∥DC，∴∠EFC +∠DCF = 180°. ∴∠EFC = 90°.∴∠BDC = 90°.5. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合，则这个旋转角度至少为( ) A．30° B．90° C．120° D．180°C6.下列说法不正确的是（ ）A. 任何一个具有对称中心的四边形都是平行四边形B. 平行四边形既是轴对称图形，又是中心对称图形C. 线段、平行四边形、矩形、菱形、正方形都是中心对称图形D. 正三角形、矩形、菱形、正方形都是轴对称图形，且对称轴都不止一条.B7. 轴对称图形的对称轴将图形面积二等分，中心对称图形过对称中心的直线将图形面积二等分.请用学过的知识将下图所示的图形面积分成相等的两部分.（1）解：如图所示.（2）8. 已知点 P (－1－2a，2a－4) 关于原点的对称点在第一象限，则整数 a 的值为 (　　)A．1B．0C．0 或 1D．0 或 1 或 2C 解：①∵△ABC绕A点逆时针旋转50°得到△AB′C′，∴BC＝B′C′．故①正确；②∵△ABC绕A点逆时针旋转50°，∴∠BAB′＝50°．∵∠CAB＝20°，∴∠B′AC＝∠BAB′﹣∠CAB＝30°．∵∠AB′C′＝∠ABC＝30°，∴∠AB′C′＝∠B′AC．∴AC∥C′B′．故②正确；③在△BAB′中，AB＝AB′，∠BAB′＝50°，∴∠AB′B＝∠ABB′＝（180°﹣50°）/2＝65°．∴∠BB′C′＝∠AB′B+∠AB′C′＝65°+30°＝95°．∴CB′与BB′不垂直．故③不正确；④在△ACC′中，AC＝AC′，∠CAC′＝50°，∴∠ACC′＝（180°﹣50°）/2＝65°．∴∠ABB′＝∠ACC′．故④正确．∴①②④这三个结论正确．故选：B．如图，已知△ABC中，∠CAB＝20°，∠ABC＝30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC＝B′C′，②AC∥C′B′，③C′B′⊥BB′，④∠ABB′＝∠ACC′，正确的有（　　）A．①②③ B．①②④ C．①③④ D．②③④