





鲁教版(五四学制)(2024)八年级上册4 多边形的内角与外角和获奖ppt课件
展开多边形的内角和正多边形的内角和
三角形的内角和是多少?
思考 我们知道,三角形的内角和等于180°,正方形、长方形的内角和都 等于360°.那么,任意一个四边形的内角和是否也等于360°呢?你能利用 三角形内角和定理证明四边形的内角和等于360°吗?
任意四边形的内角和等于多少度?你是怎样得到的?
2×180 º=360 º
4×180 º-360º=360 º
四边形的内角和是360º
3×180 º-180º=360 º
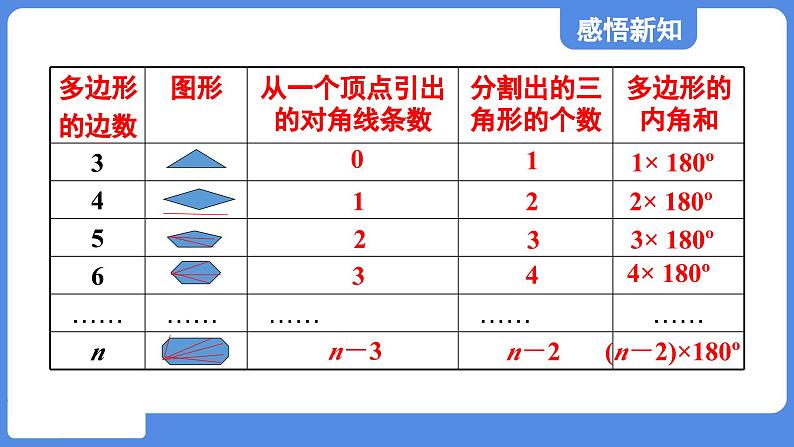
一般地,从n边形的一个顶点出发,可以作(n - 3)条对角线,它们将n边形分为(n - 2)个三角形,n边形的内角和等于180°×(n - 2).
把一个多边形分成几个三角形,还有其他分法吗?由新的分法,能得出多边 形内角和公式吗?
1. 由n 边形的内角和公式(n-2)·180°可知,n边形的内角和一定是180°的整数倍.2. 多边形的内角和随边数的变化而变化,边数每增加1,内角和就增加180° .
∵四边形的内角和为(4-2)×180°=360°,∴∠B=360°-(∠A+∠C+∠D)=360°-280°=80°.
在四边形ABCD中,若∠A+∠C+∠D=280°,则∠B的度数是( )A.80° B.90° C.170° D.20°
已知边数求内角和,可直接代入内角和公式:n边形内角和等于(n-2)×180°求解.
如图,在四边形ABCD中,∠A+∠C=180°.∠B 与∠D有怎样的关系?
∵ ∠A+∠B+∠C+∠D=(4-2)×180°=360°,∴∠B+∠D=360°-(∠A+∠C)=360°-180°=180°.
如果四边形一组对角互补,那么另一组对角也互补.
内角和为540°的多边形是( )
如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )A.①② B.①③ C.②④ D.③④
将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A.360° B.540° C.720° D.900°
将一个n边形变成(n+1)边形,则内角和将( )A.减少180° B.增加90° C.增加180° D.增加360°
一个多边形除一个内角外其余内角的和为1 510°,则这个多边形对角线的条数是( )A.27 B.35 C.44 D.54
一个多边形截去一个角后,形成一个新多边形的内角和是1 620°,则原来多边形的边数是( )A.10 B.11 C.12 D.以上都有可能
想一想正三角形(等边三角形)、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?
议一议剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
正n边形的每个内角的度数为
若一个多边形的内角和是1 260°,则这个多边形的边数是________.
设这个多边形的边数为n,由题意知,(n-2)×180°=1 260°,解得n=9.
(1)已知多边形的内角和求边数n的方法:根据多边形内角和公式列方程:(n-2)×180°=内角和,解方程求出n,即得多边形的边数;(2)已知正多边形每个内角的度数k求边数n的方法:根据多边形内角和公式列方程:(n-2)×180°=kn,解方程求出n,即得多边形的边数.
如图,求∠A+∠ABC+∠C+∠D+∠E+∠F的度数.
要求不规则图形的各个角的度数和,就是想办法在不规则图形中找规则图形,然后把不规则图形的角通过已学的相关知识(本例中三角形外角的性质)转移到规则的图形中去,即把所求的六个角的和转移到四边形BEFG中去.
在四边形BEFG中,∵∠EBG=∠C+∠D,∠BGF=∠A+∠ABC,∴∠A+∠ABC+∠C+∠D+∠E+∠F=∠BGF+∠EBG+∠E+∠F=360°.
(1)化不规则为规则是转化思想中一种常见的方法,它主要经历了两步:第一步找规则图形,第二步将不规则图形的角转化到规则图形中;关键是找规则图形.这类题一般有不同的解法,如本例还可以将四边形DEFH作为基础四边形,请读者自己完成其解法.(2)若图中没有已知的规则图形,则需通过作辅助线构造规则图形.
小彬求出一个正多边形的一个内角为145°. 他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
不正确.理由:假设是正n边形,由多边形的内角和定理,得(n-2)×180°=n×145°,解得n= ,不是整数,所以不正确.
若正多边形的一个内角是150°,则该正多边形的边数是( )A.6 B.12 C.16 D.18
若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )A.7 B.10 C.35 D.70
练点1 多边形的内角和
1. [新考向·传统文化]陕北剪纸兼备了我国北方剪纸的粗犷大 气、写意豪放和南方剪纸的工巧细致、写实秀美的特点, 某剪纸图案的外轮廓为八边形,则这个八边形的内角和为 ( C )
2. [2024·济宁月考]一个多边形的内角和的度数可能是 ( B )
n 边形的内角和为( n -2)×180°,即多边形的内角 和一定是180°的整数倍,A,C,D选项的度数不能被 180°整除,B选项的度数可被180°整除.
3. [母题·教材P145习题T2·2023·济宁]一个多边形的内角和是 540°,则这个多边形是 边形.4. [2023·重庆]若七边形的内角中有一个角为100°,则其余 六个内角之和为 .
(1)正n边形的每个内角都相等,都等于 (2)n边形的内角和与边数有关,每增加一条边,内角和就增加180°.(3)利用公式,已知n边形的边数可求内角和,同样已知内角和也可求边数.
鲁教版 (五四制)八年级上册第三章 数据的分析4 数据的离散程度教课课件ppt: 这是一份鲁教版 (五四制)八年级上册<a href="/sx/tb_c99044_t3/?tag_id=26" target="_blank">第三章 数据的分析4 数据的离散程度教课课件ppt</a>,共15页。PPT课件主要包含了Contents,问题情境,课堂小结,合作探究,例题演示,巩固练习,问题解决,想一想,概念展示,深入探究等内容,欢迎下载使用。
初中数学人教版八年级上册11.3.2 多边形的内角和评课课件ppt: 这是一份初中数学人教版八年级上册11.3.2 多边形的内角和评课课件ppt,共35页。PPT课件主要包含了学习目标,新课导入,复习引入,新知探究,都是360°,n-3,n-2,n-2×180°,多边形分割成三角形,转化思想等内容,欢迎下载使用。
鲁教版 (五四制)八年级上册4 多边形的内角与外角和完美版课件ppt: 这是一份鲁教版 (五四制)八年级上册4 多边形的内角与外角和完美版课件ppt,文件包含鲁教版五四制数学八上《多边形的内角和与外角和2》课件pptx、鲁教版五四制数学八上《多边形的内角和与外角和2》教案doc等2份课件配套教学资源,其中PPT共14页, 欢迎下载使用。













