中职数学高教版（2021）拓展模块一 上册4.3.2 直线与平面垂直一等奖ppt课件

这是一份中职数学高教版（2021）拓展模块一 上册4.3.2 直线与平面垂直一等奖ppt课件，共18页。PPT课件主要包含了学习目标，创设情境生成问题，据此有如下定义，调动思维探究新知，巩固知识典型练习，根据该定理可以证明，巩固知识典例练习，巩固练习提升素养，课堂小结，作业布置等内容，欢迎下载使用。

某型号无人机如图所示,其每根螺旋桨(如BC)与旋转轴 AB 均垂直,垂足是B.设螺旋桨旋转时构成的平面为α,显然,无人机的每根螺旋桨都在平面α内.试问,平面α与旋轴 AB 之间有怎样的位置关系？
容易看出,平面α内经过点B的螺旋桨所在直线都与旋转轴 AB 垂直.对于平面α内不过点B的任意一条直线,它一定与平面α内过点B的某条直线平行.由异面直线所成角的定义可知,这条直线也与旋转轴AB 垂直.因此,平面α内的每一条直线都与AB 垂直.
  如果一条直线和一个平面内的任何一条直线都垂直，那么称这条直线和这个平面互相垂直.这条直线称为这个平面的垂线,这个平面称为这条直线的垂面,直线与平面的交点称为垂足.直线l与平面α垂直记作l ⊥α.
如图所示,若l⊥α,m⊆α,根据直线与平面垂直的定义可知l⊥m.这是利用“直线与平面垂直”推出“直线与直线垂直”的主要方法.
画竖直的直线与水 平平面垂直时,应 将直线画成与表示平面的平行四边形的横边垂直．
在日常生活和生产中,常常需要判断直线与平面的垂直关系.例如,国旗的旗杆与地面垂直、建筑的立柱与地面垂直等.但是,判断直线与平面内每一条直线都垂直是很难做到的.
经过观察研究,人们发现以下判定直线与平面垂直的方法：
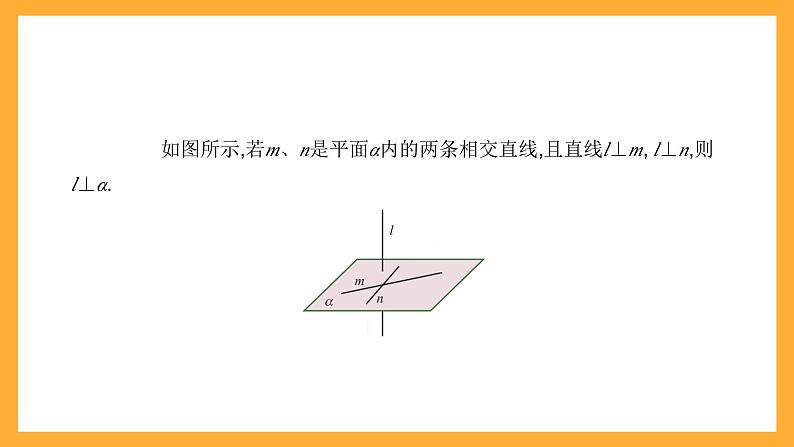
  直线与平面垂直的判定定理  如果一条直线与平面内的两条相交直线都垂直,那么这条直线与这个平面垂直.
  如图所示,若m、n是平面α内的两条相交直线,且直线l⊥m, l⊥n,则l⊥α.
典例1 四个面都是正三角形的四面体称为正四面体.已知正四面体ABCD,如图所示.求证：BD⊥AC.
典例2  证明: 如果两条平行线中有一条垂直于一个平面，那么另一条也垂直于这个平面.  已知: m∥n,m⊥α,如图所示.  求证: n⊥α.
 证明: 在平面α内任取两条相交直线c和d ,因为 m⊥α,c⊆α,d ⊆ α,所以m⊥c,m⊥d. 又m∥n,故n⊥c,n⊥d, 根据直线与平面垂直的判定定理,由c与d相交,n⊥α.
例2是直线与平面垂直的另一个判定定理.
可以证明,例2中所述命题的逆命题也成立.如图所示若m⊥α, n⊥α,则m∥n.
  直线与平面垂直的性质定理  如果两条直线都垂直于同一个平面,那么这两条直线平行. 
 在空间中经过一点有且只有一条直线与已知平面垂直. 
典例3 如图所示,已知一条直线l和平面α平行,过直线l上任意两点A、B分别引平面α的垂线 AA' 、BB',垂足分别为A' 、B'. 求证: AA'=BB'. 
 证明:因为 AA'⊥α, BB'⊥α,所以AA'∥ BB'. 设经过直线AA'、BB'的平面为β,则β∩α=A'B'.  由l∥α ,可知l∥A'B' ,因此四边形AA'B'B  为平行四边形,所以AA'=BB'. 
长方体ABCD-A1B1C1D1中（如图），直线AA1与平面ABCD垂直吗？为什么？
解　因为长方体ABCD-A1B1C1D1中，侧面ABB1A1、AA1D1D都是长方形，所以AA1⊥AB，AA1⊥AD．且AB和AD是平面ABCD内的两条相交直线．由直线与平面垂直的判定定理知，直线AA1⊥平面ABCD．
1. 判断下列命题的真假. （1）如果直线m垂直于平面α内的无数条直线，那么m⊥α;  （2）如果l⊥m,且m⊆α, n⊆α,那么l⊥α;  （3）如果l⊥α, m⊥α,那么l⊥m.
2.已知如图,PO⊥α,垂直为O, PA∩α=A,m⊆α,且m⊥OA.求证: m⊥PA.
3. 如果l⊥α,m//α,求证: l⊥m. 4. 己知线段AB、CD 位于平面α的同侧, AB ⊥α, DC⊥α, 垂足分别为 B、C,AB=DC.求证: AD=BC.
5. 某中职学校建设新校区时,修建了升旗台,用于开展爱国主义教育活动.技术人员在安装旗杆时,要保证旗杆与地面垂直.请你帮忙设计一个方案以确保旗杆与地 面垂直.
(1) 读书部分： 教材章节4.3.2； (2) 书面作业： P131习题4.3的1,5,6.
数学是一种别具匠心的艺术