高教版（中职）基础模块下册第9章 立体几何9.4 直线与直线、直线与平面、平面与平面垂直的判定与性质9.4.2 直线与平面垂直的判定与性质多媒体教学ppt课件

这是一份高教版（中职）基础模块下册第9章 立体几何9.4 直线与直线、直线与平面、平面与平面垂直的判定与性质9.4.2 直线与平面垂直的判定与性质多媒体教学ppt课件，共24页。PPT课件主要包含了创设情境兴趣导入，能作几条，巩固知识典型例题，运用知识强化练习，动脑思考探索新知，理论升华整体建构，自我反思目标检测等内容，欢迎下载使用。

9．4　直线与直线、直线与平面、平面与平面垂直的判定与性质
演示并画出两条相交直线垂直与两条异面直线垂直的位置
关系，并回答：经过空间任意一点作与已知直线垂直的直线，
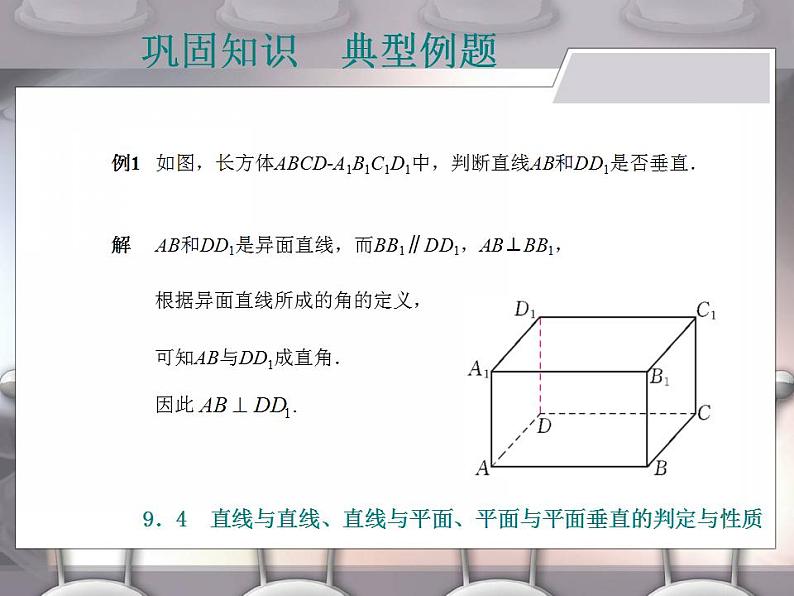
例1 如图，长方体ABCD-A1B1C1D1中，判断直线AB和DD1是否垂直．
解　 AB和DD1是异面直线，而BB1∥DD1，AB⊥BB1，
根据异面直线所成的角的定义，
可知AB与DD1成直角．
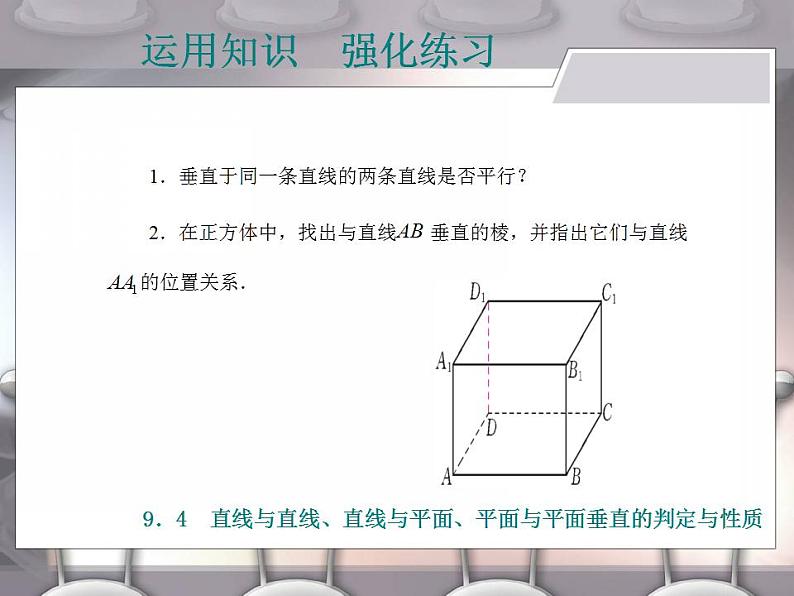
1．垂直于同一条直线的两条直线是否平行？
2．在正方体中，找出与直线
垂直的棱，并指出它们与直线
如图所示，检验一根圆木柱和板面是否垂直．工人师傅的做法是，
把直角尺的一条直角边放在板面上，看曲尺的另一条直角边是否和圆
木柱吻合，然后把直角尺换个位置，照样再检查一次（应当注意，直角
尺与板面的交线，在两次检查中不能为同一条
直线）．如果两次检查，圆木柱都能和直角尺
的直角边完全吻合，就判定圆木柱和板面垂直．
直线与平面垂直的判定方法：
如果一条直线与一个平面内的两条相交直线都垂直，那
么这条直线与这个平面垂直．
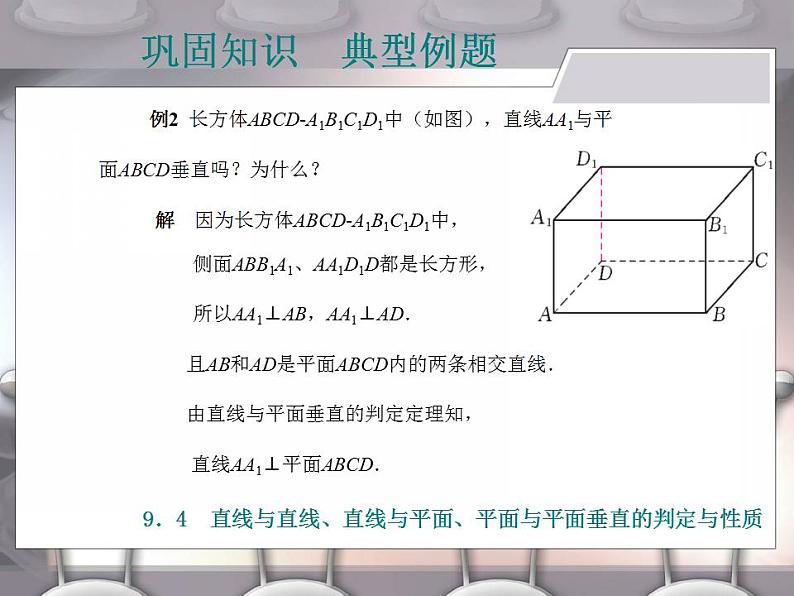
例2 长方体ABCD-A1B1C1D1中（如图），直线AA1与平
面ABCD垂直吗？为什么？
解　因为长方体ABCD-A1B1C1D1中，
侧面ABB1A1、AA1D1D都是长方形，
所以AA1⊥AB，AA1⊥AD．
且AB和AD是平面ABCD内的两条相交直线．
由直线与平面垂直的判定定理知，
直线AA1⊥平面ABCD．
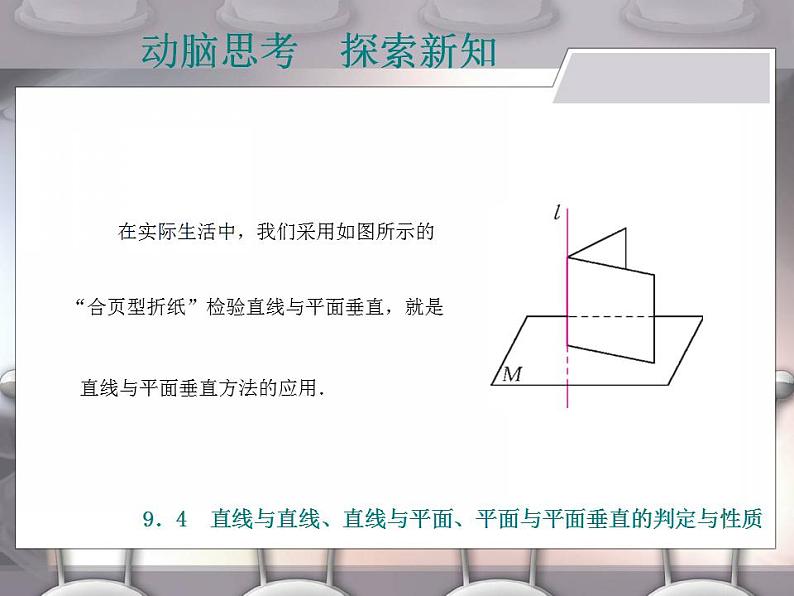
在实际生活中，我们采用如图所示的
“合页型折纸”检验直线与平面垂直，就是
直线与平面垂直方法的应用．
观察道路边的电线杆可以发现它们都垂直于地面，并且
这些电线杆是平行的．这一事实启发我们得出直线与平面垂
直线和平面垂直的性质：
垂直于同一个平面的两条直线互相平行．
如果两条平行直线中的一条垂直于一个
平面，那么另一条也垂直于这个平面吗？为
直线AE与CD交于点E．
在直角三角形ACE中，因为AE＝BD＝5 cm，
CE＝CD＋DE＝CD＋AB＝8 + 4 =12（cm），
1．一根旗杆AB高8 m，它的顶端A挂两条10 m的绳子，拉紧绳子并把它们的两个下端固定在地面上的C、D两点，并使点C、D与旗杆脚B不共线，如果C、D与B的距离都是6 m，那么是否可以判定旗杆AB与地面垂直，为什么？
两个平面相交，如果所成的二面角是直二面角，那么称这两个平面
画表示两个互相垂直平面的图形时，一般将两个平行四边形的一组
对边画成垂直的位置，可以把直立的平面画成矩形（图（1）），也可以
把直立的平面画成平行四边形（图（2））．
建筑工人在砌墙时，把线的一端系一个铅锤，另一端用砖压在墙壁
面上（如图），观察系有铅锤的线与墙面是否紧贴（在铅锤处应有一空
隙），即判断所砌墙面是否经过地面的垂线，以此保证所砌的墙面与地
平面与平面垂直的判定方法：
一个平面经过另一个平面的垂线则两个平面垂直．
例4 　在正方体ABCD-A1B1C1D1（如图）中，判断平面B1AC与
平面B1BDD1是否垂直．
解 在正方体ABCD-A1B1C1D1中，
B1B⊥平面ABCD，所以BB1⊥AC，
在底面正方形ABCD中，BD⊥AC，
因此AC⊥平面BB1D1D，
平面与平面垂直的性质：
如果两个平面垂直，那么一个平面内垂直于交线的直线与另一个平面垂直．
例5　如图所示，平面α⊥平面β， AC在平面α内，
且AC⊥AB，BD在平面β内，且BD⊥AB，AC＝12 cm，
AB＝3 cm，BD＝4 cm．求CD的长．
又由于BD⊥AB，所以在直角三角形ABD中，
故 AD＝5（cm）．
故 CD＝13（cm）．
2．如图所示，检查工件相邻的两个面是否垂直时，只要用曲尺的一边
卡在工件的一个面上，另一边在工件的另一个面上转动一下，观察尺边是
否和这个面密合就可以了，为什么？
一根旗杆AB高8 m，它的顶端A挂两条10 m的绳子，拉紧绳子并把它们的两个下端固定在地面上的C、D两点，并使点C、D与旗杆脚B不共线，如果C、D与B的距离都是6 m，那么是否可以判定旗杆AB与地面垂直，为什么？