


数学拓展模块一 上册4.3.1 直线与平面平行完美版ppt课件
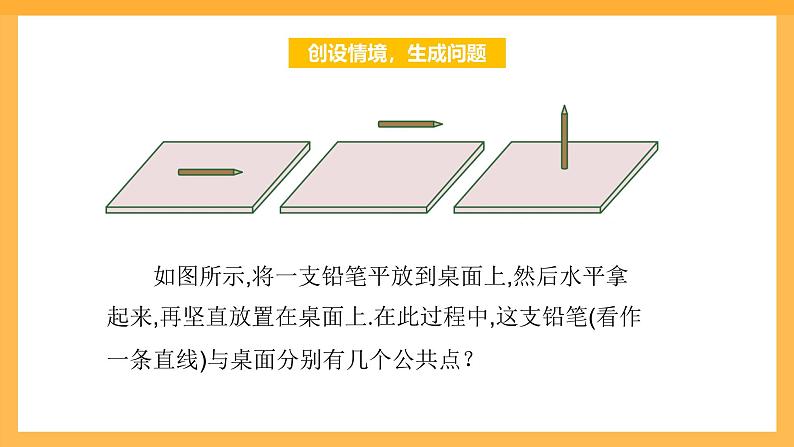
展开如图所示,将一支铅笔平放到桌面上,然后水平拿起来,再坚直放置在桌面上.在此过程中,这支铅笔(看作一条直线)与桌面分别有几个公共点?
容易看出,当笔平放在桌面上时,它与桌面有无数多个公共点;将笔水平拿起,它与桌面没有公共点; 当笔竖直放置时,它与桌面只有一个公共点.事实上,根据公理2,当一条直线与一个平面有两个公共点时,这条直线上的所有点都在这个平面内.除此之外,直线与平面或者只有1个公共点,或者没有公共点.因此,直线与平面有三种 位置关系.
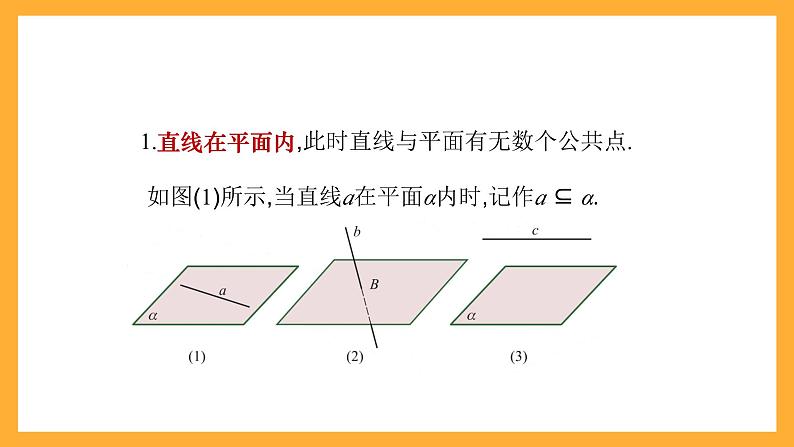
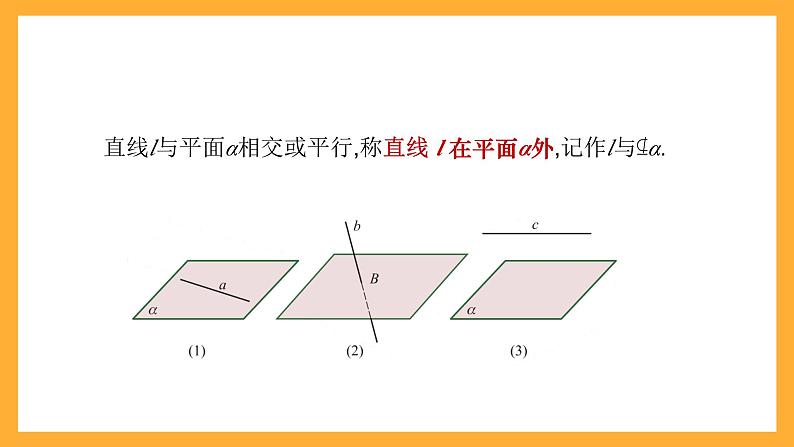
如图(1)所示,当直线a在平面α内时,记作a ⊆ α.
1.直线在平面内,此时直线与平面有无数个公共点.
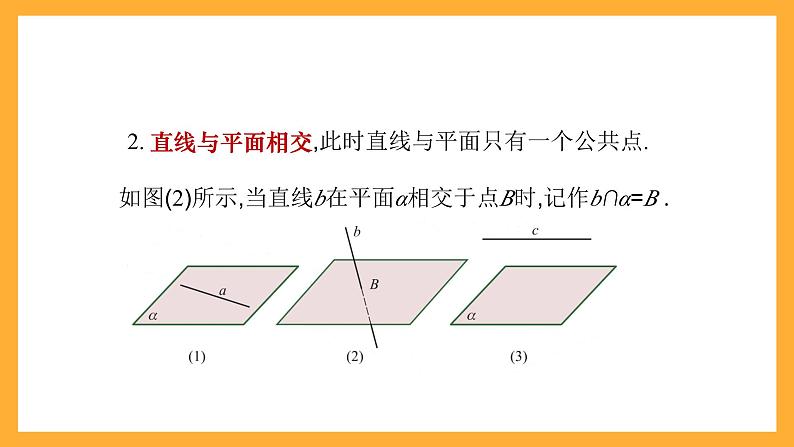
如图(2)所示,当直线b在平面α相交于点B时,记作b∩α=B .
2. 直线与平面相交,此时直线与平面只有一个公共点.
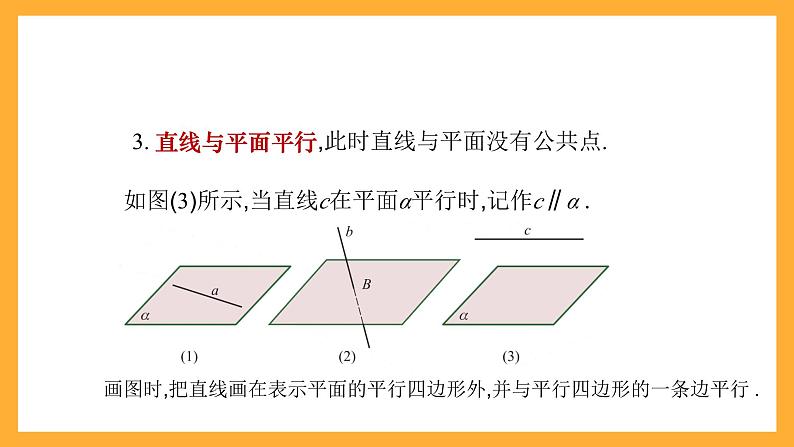
3. 直线与平面平行,此时直线与平面没有公共点.
如图(3)所示,当直线c在平面α平行时,记作c∥α .
画图时,把直线画在表示平面的平行四边形外,并与平行四边形的一条边平行 .
直线l与平面α相交或平行,称直线 l 在平面α外,记作l与⊈α.
4.3.1 直线与平面平行
如图所示,一本打开的书的封面右边沿所在直线m已经不在书内页所在平面α内,那么,m与α是相交还是平行呢?
观察发现,书脊所在直线n是封面所在平面与书内页所在平面的交线,且m∥n.
能否通过m∥n来判断直线m与平面α之间的位置关系呢?
直线与平面平行的判定定理 如果平面外的一条直线与这个平面内的一条直线平行,那么这条平面外直线与这个平面平行.
一般情形为,m⊈α,n⊆α,且m∥n,如图(1)所示. 假设直线m与平面α相交,记交点为点P,如图(2)所示. 由m∥n知P∉n.根据异面直线判定定理,m与n是异面直线,这与m∥n矛盾.故直线 m 与平面α不相交,从而m∥α.
典例1 如图所示,在棱柱ABCD-A1B1C1D1中: (1)与平面AC平行的棱所在直线有哪些? (2)判断 AA1与平面DBB1D1的位置关系.
(1)因为棱柱各侧面均为平行四边形,所以A1B1∥AB. 又因为A1B1⊆平面AC,AB ⊆平面AC,所以 A1B1 ∥平面AC ;同理可知,直线B1C1、C1D1、A1D1均与平面AC平行. 因此,与平面AC平行的棱所在直线有A1B1、B1C1、C1D1、A1D1. (2)因为 AA1∥BB1,且AA1⊈平面 DBB1D1,BB1⊆平面DBB1D1,所以AA1//平面DBB1D.
典例2 在空间四边形ABCD 中,点E、F分别是AB、AD 的中点,如图所示,求证:EF//平面BCD.
证明:连接E、F.因为E、F分别是 AB、AD 的中点,所以EF//BD. 又因为E⊈平面BCD,BD⊆平面BCD,所以BF//平 面 BCD.
既然直线与直线的平行可以用来判定直线与平面平行,那么能否利用直线与平面的平行来判定直线与直线平行呢?
如图(1)所示, m∥α, m⊆β,α∩β=n.那么, m与n是什么位置关系?
直线与平面平行的性质定理 如果一条直线和一个平面平行, 那么经过这条直线的任一平面和这个平面的交线与这条直线平行.
显然,m与n共面于平面B内,则n与n要么相交,要么平行.若m与n相交,且交点为P,如图(2)所示,则P也是直线m与平面α的交点,这与条件m//α相矛盾.所以m//n.于是,有下面的结论:
典例3已知n //m,m//α,n⊈ α ,求证:n //α.
1. 判断下列命题的真假,并说明理由. (1)如果m//n,n⊆α,那么m//α; (2)如果m//n,m⊈α,那么m//α; (3)如果m//α,n⊆α,那么m//n; (4)如果m//α,m⊆β, α∩β=n,那么m//n.
2. 填空题. (1) 如果一条直线与一个平面平行,那么这条直线与这个平面有 个公共点; (2) 如果一条直线与一个平面有两个公共点,那么它们的位置关系是 ,此时直线与平面面共有 个公共点: (3)如果一条直线与一个平面相交,那么它们有 个公共点; (4)如果一条直线与一个平面平行,那么这条直线与平面内的 条直线平行.
4. 已知正方体ABCD-A1B1C1D1.求证: (1) CD∥平面A1C1; (2) A1C1∥平面AC.
5. 某中职学校机械加工技术专业学生在加工长方体 ABCD-A1B1C1D1形状的零件时,如图所示,需要沿着
由上底面A1C1上的点E与棱AD确定的平面将零件切开.切削前需在长方体相应的面上画出轮廓线,试问该怎样画这个轮廓线?经过点E所画的直线与底面AC 是什么位置关系?
(1) 读书部分: 教材章节4.3.1; (2) 书面作业: P131习题4.3的3.
数学是一种别具匠心的艺术
数学4.3.1 直线与平面平行一等奖ppt课件: 这是一份数学<a href="/sx/tb_c4053653_t3/?tag_id=26" target="_blank">4.3.1 直线与平面平行一等奖ppt课件</a>,共23页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,情境导入,线面位置关系,观察下列图片并思考,直线与平面平行,直线在平面内等内容,欢迎下载使用。
中职数学高教版(2021·十四五)拓展模块一(上册)第4章 立体几何4.3 直线与平面的位置关系4.3.1 直线与平面平行优秀课件ppt: 这是一份中职数学高教版(2021·十四五)拓展模块一(上册)<a href="/sx/tb_c4053653_t3/?tag_id=26" target="_blank">第4章 立体几何4.3 直线与平面的位置关系4.3.1 直线与平面平行优秀课件ppt</a>,共23页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,情境导入,线面位置关系,观察下列图片并思考,直线与平面平行,直线在平面内等内容,欢迎下载使用。
中职数学4.3.1 直线与平面平行教案配套课件ppt: 这是一份中职数学<a href="/sx/tb_c4035799_t3/?tag_id=26" target="_blank">4.3.1 直线与平面平行教案配套课件ppt</a>,文件包含43直线与平面的位置关系课件pptx、43直线与平面的位置关系教案docx等2份课件配套教学资源,其中PPT共49页, 欢迎下载使用。












