人教版（2024）七年级上册（2024）2.3 有理数的乘方教学课件ppt

这是一份人教版（2024）七年级上册（2024）2.3 有理数的乘方教学课件ppt，共22页。PPT课件主要包含了第2章有理数，第1课时乘方，×2×2，cm2，cm3，都是相同因数的乘法，平方厘米，立方厘米，的平方，的二次方等内容，欢迎下载使用。

2.3.1 乘 方
2.3 有理数的乘方
中国古代文人墨客的笔下充满了有意境的诗句.如陶渊明曾写到“勤学如春起之苗，不见其增，日由所长；辍学如磨刀之石，不见其损，日有所亏”
知识点： 乘方
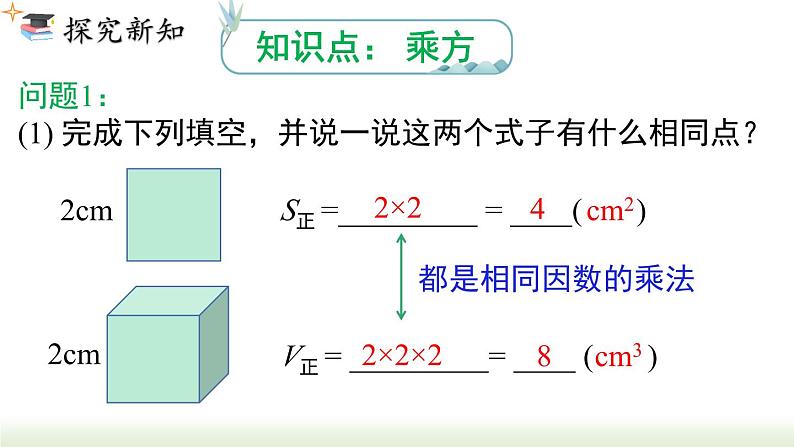
问题1：(1) 完成下列填空，并说一说这两个式子有什么相同点？
S正 =_________ = ____( )
V正 = _________= ____ ( )
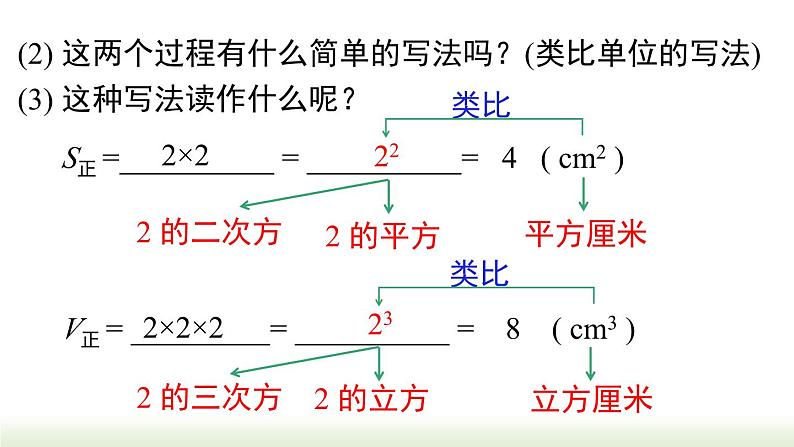
(2) 这两个过程有什么简单的写法吗？(类比单位的写法)
S正 =__________ = __________= 4 ( cm2 )
V正 = _________= __________ = 8 ( cm3 )
(3) 这种写法读作什么呢？
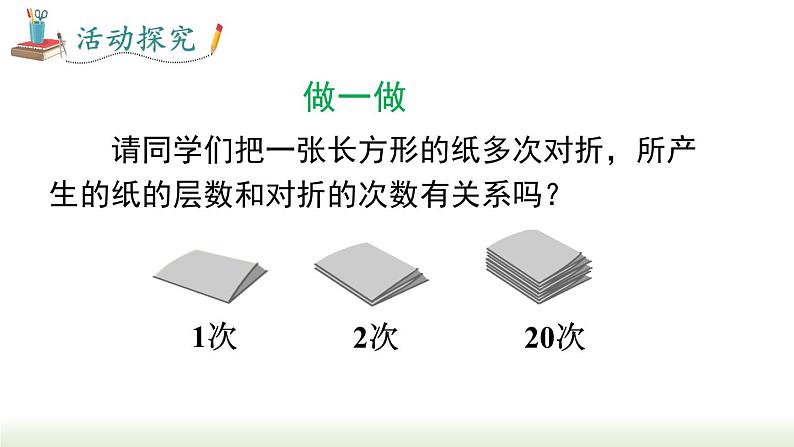
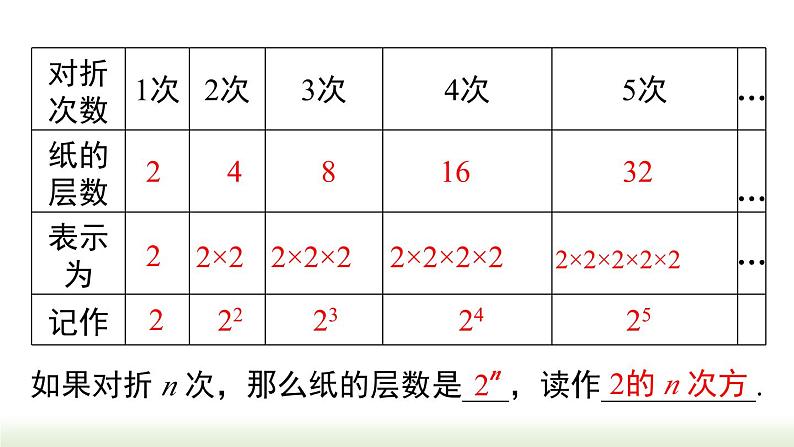
请同学们把一张长方形的纸多次对折，所产生的纸的层数和对折的次数有关系吗？
如果对折 n 次，那么纸的层数是___，读作__________.
问题2：类比以上研究，完成下列填空.
(1) (-2)×(-2)×(-2)×(-2)×(-2) 记作________，读作_____________；
根据问题 1、问题 2 你能总结出什么规律？
(-2)4 与 -24 一样吗？为什么？
一般地，n 个相同的因数 a 相乘，即 ，
记作_____，读作___________.
表示 n 个 a 相乘
求 n 个相同因数的积的运算叫做乘方，乘方的结果叫幂.
(1) (－5)2 的底数是_____，指数是_____，(－5)2表示 2 个_____相乘，读作_____的 2 次方，也读作 －5 的_____________.(2) 表示 个 相乘，读作 的 次方，也读作 的 次幂，其中 叫做 ，6 叫做 .
解：(1) (-4)3 = (-4)×(-4)×(-4) = -64.
(2) (-2)4 = (-2)×(-2)×(-2)×(-2) = 16.
(1) (－4)3； (2) (－2)4； (3) 　．
探究一：从例1，你发现负数的幂的正负有什么规律吗？
当指数是________数时，负数的幂是_______数；
当指数是________数时，负数的幂是_______数.
正数或 0 的任何正整数次幂的正负有什么规律吗？
1. 负数的奇次幂是负数，负数的偶次幂是正数；
2. 正数的任何正整数次幂都是正数， 0 的任何正整数次幂都是 0.
根据有理数的乘法法则可以得出：
(1) -(-3)2 = ； (2) -32 = ；
(3) (-5)3 = ； (4) 0.13 = ；
(5) (-1)9 = ； (6) (-1)12 = ；
例2 用计算器计算 (-8)5 和 (-3)6.
所以(-8)5 = -32768，(-3)6 = 729.
1.01365≈________；
如果我们把 1 看成每天应完成的学习量，
0.99365≈________；
1.01 表示比前一天多做了一点儿、多学了一点儿，0.99 表示比前一天少做了一点、少学了一点儿. 一年 365 天，1 的 365 次方还是1；1.01 的 365 次方约为 37.8，远大于1；0.99 的 365 次方约为 0.03，远小于1.
一般地，n 个相同的因数a相乘，即
负数的奇次幂是______，负数的偶次幂是_______，正数的任何正整数次幂都是______，0 的任何正整数次幂都是_____
求 n 个相同因数的___的运算叫做乘方，乘方的结果叫____；在 an 中，a叫做____，n 叫做______
记作：__________
读作：_____________
1. 下列各组运算中，结果相等的是( )
A. -32 与 -23
B. -23 与 (-2)3
C. -32 与 (-3)2
D. (-3×2)2 与 -3×22
2. 如果一个数的 15 次幂是负数，那么这个数的 2 023 次幂是_________. (填“正数”“负数”或“0”)