第2章 有理数的运算小结与复习 人教版数学七年级上册课件

这是一份第2章 有理数的运算小结与复习 人教版数学七年级上册课件，共30页。

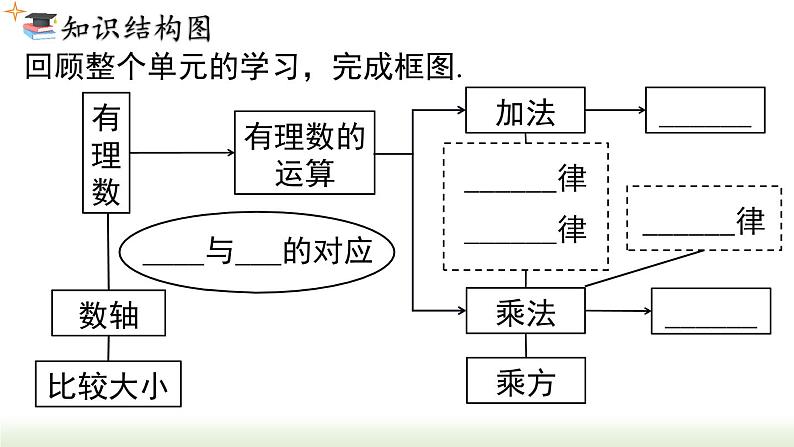
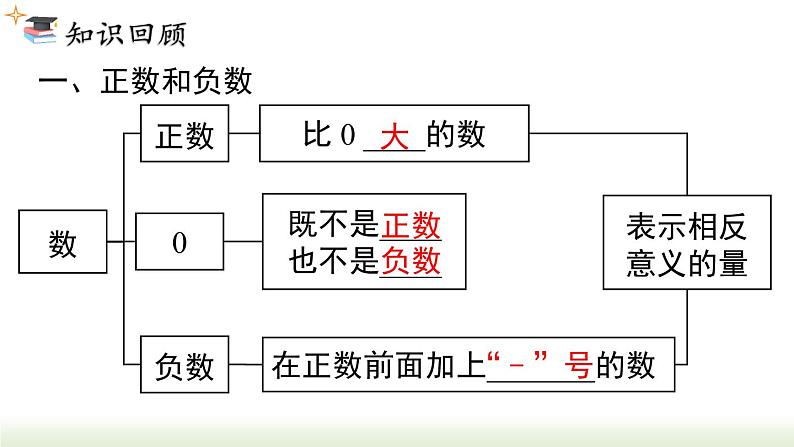
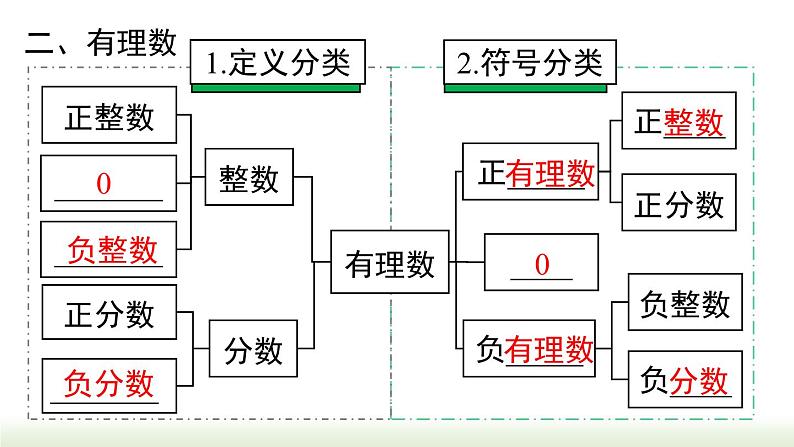
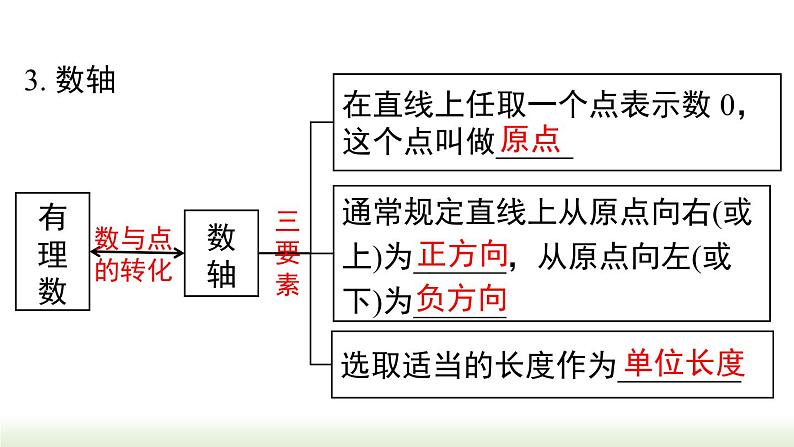
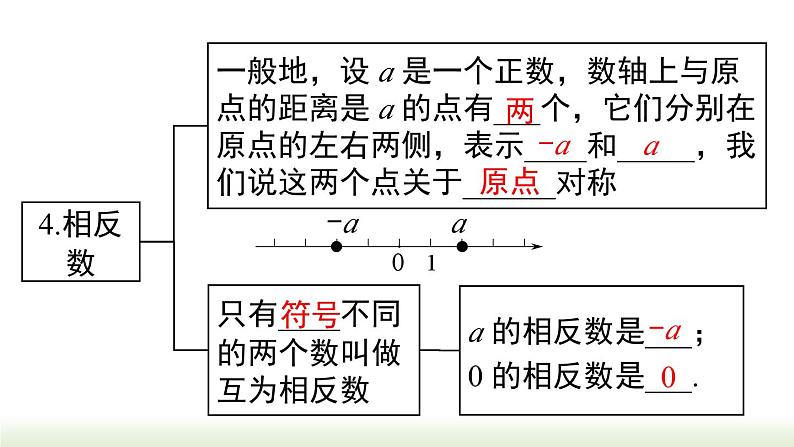
小结与复习第2章 有理数回顾整个单元的学习，完成框图.一、正数和负数既不是____也不是____在正数前面加上_______的数比 0 ____的数“﹣”号正数负数大数正数0负数表示相反意义的量二、有理数______________正分数正整数负整数0整数分数_______负分数1.定义分类有理数正_____负_________正____正分数负____负整数0有理数有理数整数分数2.符号分类3. 数轴数轴在直线上任取一个点表示数 0，这个点叫做_____选取适当的长度作为________通常规定直线上从原点向右(或上)为______，从原点向左(或下)为______原点单位长度三要素正方向负方向有理数数与点的转化4.相反数一般地，设 a 是一个正数，数轴上与原点的距离是 a 的点有___个，它们分别在原点的左右两侧，表示____和_____，我们说这两个点关于______对称只有____不同的两个数叫做互为相反数a 的相反数是___；0 的相反数是___.原点符号0a-a两-a5.绝对值一般地，数轴上表示数 a 的点与原点的____叫做绝对值有理数比较大小正数___ 0 ___ 负数；负数比较大小：绝对值大的反而____距离小如果 a ＞ 0，那么 |a| =___；如果 a = 0， 那么 |a| =___；如果 a ＜ 0，那么 |a| =___＞＞a-a06.有理数比较大小正数___ 0 ___ 负数；负数比较大小：绝对值大的反而____小＞＞法则三、有理数的运算1. 有理数的加法(1) 加法法则(2) 加法的运算律加法的交换律加法的结合律2. 有理数的减法减法法则：减去一个数，等于加上这个数的相反数.3. 有理数的乘法(1) 乘法法则(2) 乘法的运算律乘法的交换律乘法的结合律4. 有理数的除法乘法的分配律除法法则：除以一个数，等于乘这个数的倒数.(1) 先乘方，再乘除，最后加减；(2) 同级运算，从左到右进行；(3) 如有括号，先做括号内的运算，按小括号、 中括号、大括号依次进行.5. 有理数的乘方求几个相同因数的积的运算，叫做乘方.6. 有理数的混合运算四、科学记数法五、近似数1. 按照要求取近似数2. 由近似数判断精确度四舍五入到某一位，就说这个近似数精确到那一位.1. 1≤a＜10；2. n 为原数的整数位数减去 1.把大于 10 的数记成 a×10n 的形式，其中考点1： 正数与负数 例1 (铜仁校考)仔细思考以下各对量：①胜二局与负三局；②气温升高 3 ℃ 与气温为 -3℃；③盈利 3 万元与亏损 3 万元；④两场篮球比赛，甲、乙两队的比分分别为 65∶60 与 60∶65. 其中具有相反意义的量有( ) A. 1 对 B. 2 对 C. 3 对 D. 4 对分析：相反意义的量：① 胜↔负；③ 盈利↔亏损②升高↔零下；④65∶60↔60∶65不具相反意义的量：B1. ( 广东中考 ) 负数的概念最早出现在我国古代著名的数学专著《九章算术》中，如果把收入 5 元记作 ＋5 元，那么支出 5 元记作( ) A. －5 元 B. 0 元 C. ＋5 元 D. ＋10 元A×××√解析：① 0 不带“－”号，但 0 不是正数，故①错误；④ 0 ℃ 并不是表示没有温度，它介于正温度与负温度之间，故④错误.③同①，故③错误；②正数的相反数是负数，故②正确；考点2： 有理数的分类 例3 (铜仁校考)把下列各数填在相应的大括号里(填序号).① -8；② 0.275；④ 0；⑤ -1.04；⑥ -( -10 )；⑧ -( -2 ) .正数集合 ｛__________________｝；负整数集合｛__________________｝；整数集合 ｛__________________｝；负分数集合｛__________________｝.② ③⑥10 2 ⑧①④⑥⑧①⑤⑦2. ( 内蒙古期末) 下列说法①正整数和负整数统称整数②零既不是正数，也不是非负数 ③有理数除整数外，其余全是分数 ④正分数和负分数统称为分数，其中正确的有( ) A. 0 个 B. 1 个 C. 2 个 D. 3 个C考点3： 相反数、倒数、绝对值 例4 填表：3.5|-2|0-3.5-20.5-3考点4：数轴 例5 ( 自贡中考) 如图，数轴上点 A 表示的数是 2023，OA = OB，则点 B 表示的数是( )B3. ( 哈尔滨期中) 有理数 a，b，c 在数轴上的位置如图所示，化简 | b + c | + | a - c | = __________.解：因为 a＞0，b＜0，c＜0，所以 b + c＜0，a - c＞0.所以 | b + c | + | a - c | = -( b + c ) + (a - c)= -b - c + a - c = a - b - 2c a - b - 2c考点5： 有理数比较大小 解法一：将各数在数轴上表示出来，右边的大于左边的，然后从大到小排列：解法二：正数大于 0，0 大于负数，正数大于负数；两个负数，绝对值大的反而小．＞考点6： 科学记数法 例7 (保定模拟考)地球与太阳的最远距离约为 15 200 万千米，最近距离约为 14 700 万千米，两者相差的距离用科学记数法表示为( ) A. 5×102 千米 B. 5×104 千米 C. 5×106 千米 D. 5×108 千米分析：15200 - 14700 = 500 万千米 500×104 千米C5×106 千米考点7： 近似数 例7 (哈尔滨期中)用四舍五入法对 0.030 47 取近似值，精确到 0.001 的结果是( ) A. 0.0305 B. 0.04 C. 0.031 D. 0.030分析： 0.030 47 精确到 0.001 对 4 进行四舍五入0.030D5. (湖南中考) 某年，长沙市全年地区生产总值约为1 400 000 000 000 元，比上年增长 4.5%，其中数据1 400 000 000 000 用科学记数法表示为( ) A. 1.4×1012 B. 0.14×1013 C. 1.4×1013 D. 14×10116. (奉贤期中) 近似数 2.74×105 精确到______位.A千考点8： 有理数的运算 例8 计算：1. 把减法转化为加法时，要注意符号；2. 对几个有理数相加减的题目，要注意观察，将哪些数放在一起会使计算简便.注意符号问题= 21 - 27 + 30 - 10= 14. 先确定商的符号，再把绝对值相除= -2×12×12= -288. 注意：1. 底数或因数是带分数时，要先将带分数化成假分数；2. 区分 -24 与 (-2)4.答案：(1) -17.(2) 33.(3) -3.3.(2) 23 - 6×(-3) + 2×(-4)；