第2章 有理数的运算小结 人教版数学七年级上册课件

这是一份第2章 有理数的运算小结 人教版数学七年级上册课件，共19页。

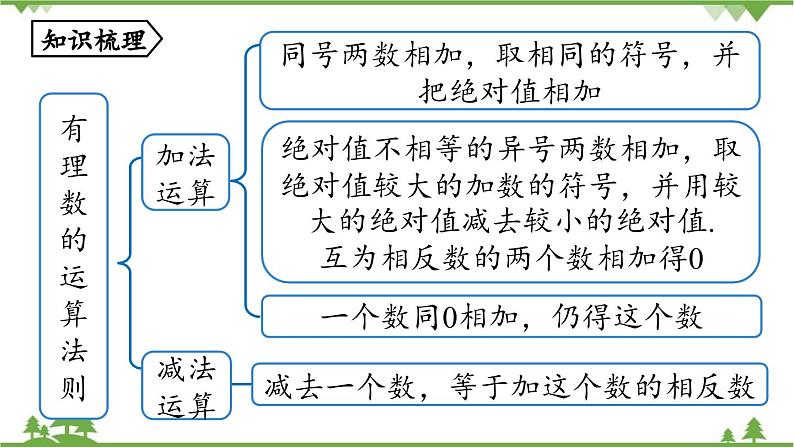
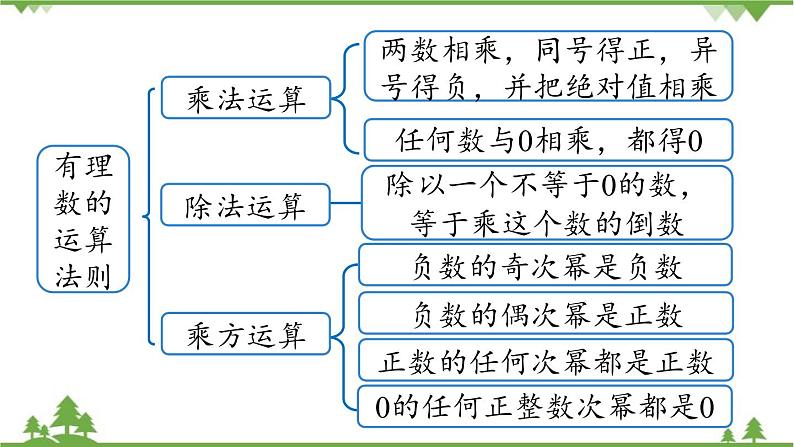
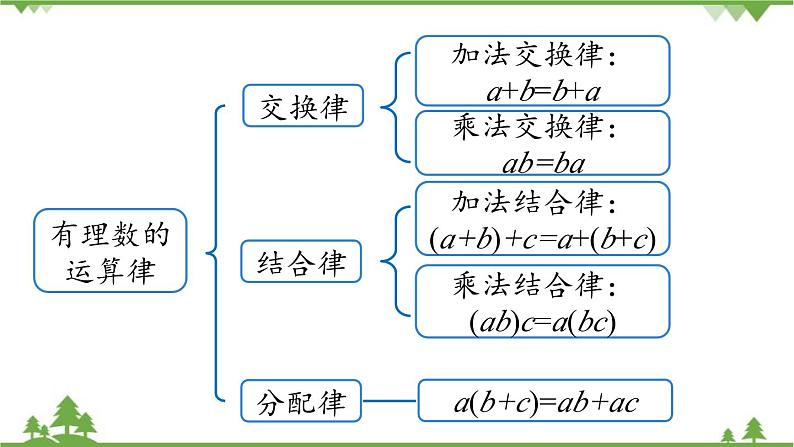
第2课时2.4 有理数小结七年级上册 RJ初中数学同号两数相加，取相同的符号，并把绝对值相加绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0一个数同0相加，仍得这个数加法运算有理数的运算法则减法运算减去一个数，等于加这个数的相反数知识梳理有理数的运算法则两数相乘，同号得正，异号得负，并把绝对值相乘任何数与0相乘，都得0负数的奇次幂是负数负数的偶次幂是正数正数的任何次幂都是正数0的任何正整数次幂都是0乘法运算除法运算除以一个不等于0的数，等于乘这个数的倒数乘方运算有理数的运算律交换律结合律加法交换律：a+b=b+aa(b+c)=ab+ac分配律乘法交换律：ab=ba加法结合律：(a+b)+c=a+(b+c)乘法结合律：(ab)c=a(bc)1.计算：  重难剖析可以统一化为分数再进行计算.1.计算：  适当运用运算律可以简化计算.1.计算：  先定号，把除法化为乘法.1.计算：  按照运算顺序进行计算.1.计算：  按照运算顺序进行计算.2.杨梅开始采摘啦！每筐杨梅以5千克为基准，超过的千克数记为正数，不足的千克数记为负数，记录如下(单位：千克)：-0.1，-0.3，+0.2，+0.3，则这4筐杨梅的总质量是( )A.19.7千克 B.19.9千克 C.20.1千克 D.20.3千克解析：根据题意，得(-0.1-0.3+0.2+0.3) +5×4=20.1(千克)，故这4筐杨梅的总质量是20.1千克.C3.观察规律：1=12；1+3=22；1+3+5=32；1+3+5+7=42；…则1+3+5+…+2019的值是 . 1 020 1004.已知 (x+3)2+|y-2|=0，z是绝对值最小的数，求(x+y)y+xyz的值.解：因为 (x+3)2+|y-2|=0，(x+3)2≥0，|y-2|≥0，所以(x+3)2=0，|y-2|=0，故x+3=0，y-2=0，所以 x=-3，y=2.因为z是绝对值最小的数，所以z=0，所以 (x+y)y+xyz=(-3+2)2+( -3)×2×0=1.1.若|x|=5，|y|=9，则x+y=  ，x-y= ．解析：因为|x|=5，|y|=9，所以x=-5，y=9或x=-5，y=-9或x=5，y=9或x=5，y=-9，则x+y=4或-14或14或-4．x-y=-14或4或-4或14．4或-14或14或-4-14或4或-4或14能力提升2.观察下列三行数：-2，4，-8，16，-32，…①0，6，-6，18，-30，…②-1，2，-4，8，-16，…③(1) 第①行的数按什么规律排列？写出第①行的第n个数.解：(1) 第①行的有理数分别是-2，(-2)2，(-2)3，(-2)4，…，故第n个数为(-2)n(n是正整数).2.观察下列三行数：-2，4，-8，16，-32，…①0，6，-6，18，-30，…②-1，2，-4，8，-16，…③(2) 第②③行数与第①行数分别有什么关系？ 2.观察下列三行数：-2，4，-8，16，-32，…①0，6，-6，18，-30，…②-1，2，-4，8，-16，…③(3) 取每行第7个数，计算这三个数的和． 3.小车司机蔡师傅某天下午的营运全是在东西走向的富泸公路上进行的，如果规定向东为正，向西为负，他这天下午的行车里程（单位：千米）如下：+14，-3，+7，-3，+11，-4，-3，+11，+6，-7，+9.(1) 蔡师傅这天最后到达目的地时，距离下午出车时的出发地多远？解：(1) 14-3+7-3+11-4-3+11+6-7+9=38(千米).答：蔡师傅这天最后到达目的地时，距离下午出车时的出发地38千米.3.小车司机蔡师傅某天下午的营运全是在东西走向的富泸公路上进行的，如果规定向东为正，向西为负，他这天下午的行车里程（单位：千米）如下：+14，-3，+7，-3，+11，-4，-3，+11，+6，-7，+9(2) 蔡师傅这天下午共行车多少千米？(2) 14+3+7+3+11+4+3+11+6+7+9=78(千米).答：蔡师傅这天下午共行车78千米.3.小车司机蔡师傅某天下午的营运全是在东西走向的富泸公路上进行的，如果规定向东为正，向西为负，他这天下午的行车里程（单位：千米）如下：+14，-3，+7，-3，+11，-4，-3，+11，+6，-7，+9(3) 若每千米耗油0.1 L，则这天下午蔡师傅用了多少升油？(3) 78×0.1=7.8(升).答：这天下午蔡师傅用了7.8升油．