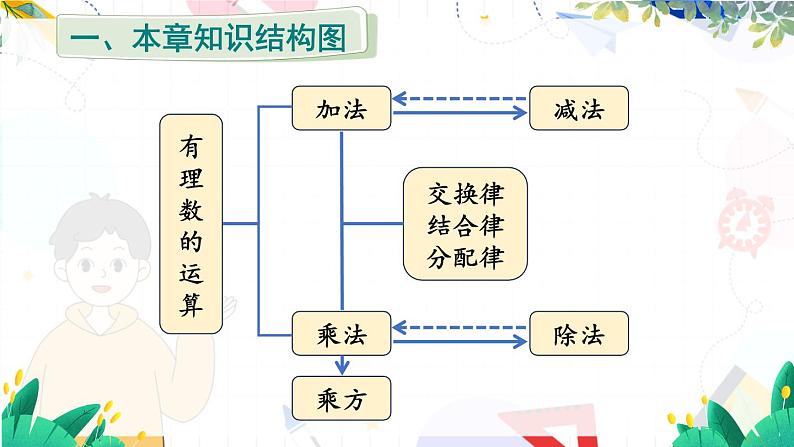
人教【2024版】七上数学 第2章 章末复习 PPT课件

这是一份人教【2024版】七上数学 第2章 章末复习 PPT课件，文件包含章末复习pptx、复习题2pptx等2份课件配套教学资源，其中PPT共44页， 欢迎下载使用。

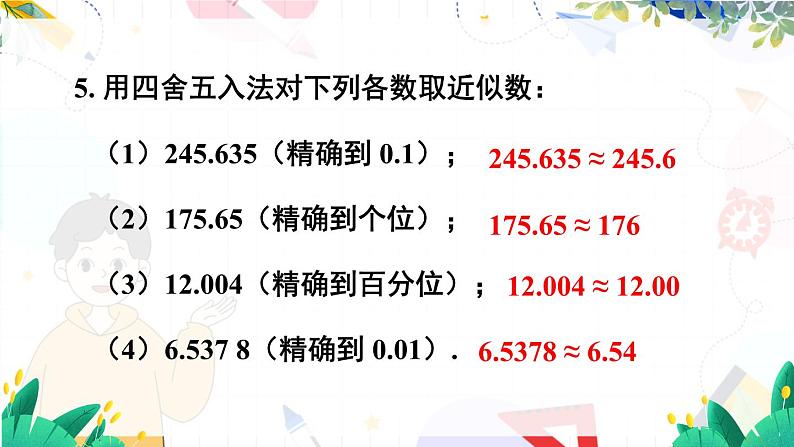
人教版·七年级上册复习题 2复习巩固1. 计算：【教材P61】（1）-150 + 250； （2）-15+(-23)；（5）(-6)×(-16)； （6）(- )×27；（3）-5-65； （4）-26-(-15)；100-38-70-1196-92. 计算：（1）6 + (- )-2-(-1.5)；（2）(-0.02)×(-20)×(-5)×4.5； （3）(-6.5)×(-2)÷(- )÷(-5)；（4）(-66)×4-(-2.5)÷(-0.1)；-95.3-289（5）(-2)2×5-(-2)3÷4；（6）-(3-5)+ 32×(1-3).22-163. 互为相反数的两个数的和是多少？互为倒数的两个数的积是多少？解：互为相反数的两数的和是 0，互为倒数的两数的积是 1.4. 用科学记数法表示下列各数：（1）100 000 000；（2）4 500 000；（3）692 400 000 000.解：（1）100 000 000 = 1×108（2）4 500 000 = 4.5×106（3）692 400 000 000 = 6.924×10115. 用四舍五入法对下列各数取近似数：（1）245.635（精确到 0.1）；（2）175.65（精确到个位）；（3）12.004（精确到百分位）；（4）6.537 8（精确到 0.01）.245.635 ≈ 245.6175.65 ≈ 17612.004 ≈ 12.006.5378 ≈ 6.546. 计算：（1）-2-|-3|； （2）|-2-(-3)|.-51综合运用7. 红、黄、蓝三支足球队进行比赛，比赛结果是：红队胜 黄队，比分为 4∶2；蓝队胜黄队，比分为 3∶1；红队 负蓝队，比分为 2∶3. 如果进球数记为正，失球数记为 负，那么三队的净胜球数各是多少？红队：(4-2) + (2-3) = 1黄队：(2-4) + (1-3) = -4蓝队：(3-1) + (3-2) = 38. 下列各数是十名学生的数学检测成绩：82，83，78，66，95，75，61，93，82，81.先估算他们的平均成绩，然后在此基础上计算平均成绩，由此检验你的估值能力.解：估算他们的平均成绩是 75，再重新记写他们的成绩：将成绩超过 75 的部分记作正数，低于 75 的部分记作负数，等于 75 的记作 0. 他们的成绩如下：7，8，3，-9，20，0，-14，18，7，6.[7 + 8 + 3 + (-9) + 20 + 0 + (-14) + 18 + 7 + 6]÷10 = 4.6，平均成绩是 75 + 4.6 = 79.69. 某文具店在一星期的销售中，盈亏情况如下表所示（记盈余为正，单位：元）.表中星期六的盈亏数被墨水涂污了，请你算出星期六的盈亏数，并说明星期六是盈利还是亏损，金额是多少.458-(-27.8-70.3 + 200 + 138.1-8 + 188) = 38 (元)答：星期六盈利，盈利了 38 元.【教材P62】10. 巡道员沿一条东西向的铁路进行巡视维护，从驻地出发先向东走了 7 km，又向东走了 3 km，然后折返向西走了 11.5 km. 此时他在驻地的什么方向？与驻地的距离是多少千米？7 km3 km11.5 km11.5-7-3 = 1.5（km）答：他在驻地的西方，与驻地的距离是 1.5 km.11. 在 0~40 ℃ 范围内，当温度每上升 1 ℃ 时，某种金属丝约伸长 0.002 mm；反之，当温度每下降 1 ℃ 时，金属丝约缩短 0.002 mm. 把 20 ℃ 的这种金属丝加热到 30 ℃，再使它冷却降温到 5 ℃，金属丝的长度经历了怎样的变化？最后的长度比原长度约伸长多少毫米？解：把 20℃ 的金属丝加热到 30℃，其伸长的长度约为0.002×(30-20) = 0.002×10 = 0.02(mm)；再把 30℃ 的金属丝冷却降温到 5℃，其缩短的长度约为0.002×(30-5) = 0.002×25 = 0.05(mm).最后的长度比原长度约伸长 0.02 + (-0.05) = -0.03(mm).12. 一年之中地球与太阳之间的距离随时间而变化，1 个天文单位是地球与太阳之间的平均距离，约为 1.496 亿千米. 试用科学记数法表示 1 个天文单位是多少千米.1.496 亿千米 = 149 600 000 km = 1.496×108 km答：一个天文单位是 1.496×108 千米。13. 结合具体的数的运算，通过特例进行归纳，然后 比较下列数的大小：拓广探索（1）小于 1 的正数 a，a 的平方，a 的立方；（2）大于 -1 的负数 b，b 的平方，b 的立方.解:（1）当a = 0.1时，a2= 0.01，a3 = 0.001，a>a2>a3.（2）当b = -0.2 时，b2 = 0.04，b3 = -0.008，b2>b3>b.14. 结合具体的数，通过特例进行归纳，然后判断下列说法 是否正确. 如果认为正确，请说明理由；如果认为错误， 请举出反例.（1）任何数都不等于它的相反数；错， 0 的相反数是其本身.（2）互为相反数的两个数的同一正偶数次幂相等；（3）如果 a 大于 b，那么 a 的倒数小于 b 的倒数.对，因为互为相反数的两个数的同一偶数次方符号相同，绝对值相等.错，例如 a = 1，b = -1，则a > b，其倒数15. 用计算器计算下列各式，将结果写在横线上：1×1=________； 11×11=_______；111×111=________； 1111×1111=__________.（1）你发现了什么？1121123211234321（2）不用计算器，你能直接写出 111 111 111×111 111 111 的结果吗？123456789876543211.从教材习题中选取；2.完成练习册本课时的习题.