初中数学人教版八年级上册12.1 全等三角形优秀复习课件ppt

这是一份初中数学人教版八年级上册12.1 全等三角形优秀复习课件ppt，共26页。PPT课件主要包含了知识梳理，体系建构，典例精析，基础巩固，综合应用，拓展延伸等内容，欢迎下载使用。

在这一章，我们深入地研究了全等三角形的性质、判定以及相关的应用，这节课我们把这章的知识整体回顾一下.
复习目标： 1．知道全等三角形的性质、判定. 2．能说出角平分线性质、判定以及它与全等三角形知识的联系. 3．灵活地运用全等三角形的性质、判定解决几何问题.
请同学们回答下列问题：（1）你能举出实际生活中运用全等形的例子吗？（2）举例说明全等三角形有什么性质？（3）从三角形的三条边对应相等、三个角对应相等中任选三个作为条件，可组合出几种情况？哪些能判定两个三角形全等？两个直角三角形全等的条件是什么？
请同学们回答下列问题：（4）学习本章后，你对角平分线有了哪些新的认识？对比角平分线的性质和判定，它们有何异同？你能用全等三角形证明角平分线的性质和判定吗？（5）你能举例说明一个几何命题的一般过程吗？
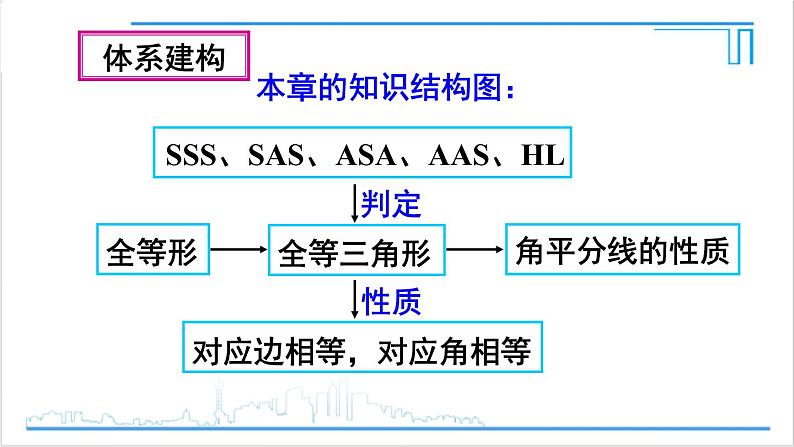
　 本章的知识结构图：
结合本章知识结构图，思考以下问题：（1）回顾本章的学习过程，全等三角形的性质和判定在本章中的重要作用是如何体现的？
　　从知识间的内在联系及知识的推理依据来分析，全等形、全等三角形、角平分线，角平分线的性质和判定等，都体现了全等三角形知识的运用；同时，全等三角形知识也是证明线段相等和角相等的重要依据．
　　回忆全等三角形、角平分线的性质和判定 的作用．
结合本章知识结构图，思考以下问题：（2）通过本章的学习，说一说证明线段相等和角相等的方法有哪些？
①巧添辅助线构造全等三角形
例1 如图，在△ABC中，AB =12，AC =8，AD是BC边上的中线，求AD的取值范围.
解：延长AD至E，使AD = DE，连接BE，CE.∵AD是BC边上的中线，∴BD = CD.在△BDE 和△CDA中，∴△BDE≌△CDA（SAS）.
解：∴BE = CA = 8. ∵AB－BE < AE < AB + BE， ∴4 < AE < 20. ∴2 < AD < 10.
②利用三角形全等解决开放性与探究性问题.
例2 如图，在△ABD和△ACE中，有下列四个条件：a. AB = AC，b. AD = AE，c.∠1=∠2，d.BD = CE.请你以其中三个条件为题设，余下的作为结论，写出一个真命题.（要求写出已知、求证及证明过程）
解：命题：如果AB = AC，AD = AE，∠1=∠2，那么BD = CE.已知：如图，△ABD和△ACE中，AB = AC，AD = AE，∠1 =∠2.求证：BD = CE.
解：证明：∵∠1=∠2，∴∠1+∠CAD=∠2+∠CAD，即∠BAD=∠CAE.在△ABD和△ACE中，∴△ABD≌△ACE(SAS).∴BD = CE.
练习1　已知：如图，∠CAB =∠DBA，AD、BC 分别是∠CAB、∠DBA 角平分线，AD、BC 相交于点O．求证：（1）△CAB ≌△DBA．
　　证明：请同学们自己写出证明过程．
练习1　已知：如图，∠CAB =∠DBA，AD、BC 分别是∠CAB、∠DBA 角平分线，AD、BC 相交于点O．求证：（2）△OCA ≌△ODB；
　　证明：由（1）得， △CAB ≌△DBA , ∴　 ∠C =∠D，CA =DB． 又　∠COA =∠DOB， ∴　△OCA ≌△ODB．
答： O 到三条直线AC、AB、BD 的距离相等．理由：略．
练习1　已知：如图，∠CAB =∠DBA，AD、BC 分别是∠CAB、∠DBA 角平分线，AD、BC 相交于点O．求证：（3）O 到三条直线AC、AB、BD 的距离有何大小关系？并说明理由．
练习2 为了促进当地旅游发展，某地要在三条公路围成的一块平地上修建一个度假村. 要使这个度假村到三条公路的距离相等，应在何处修建？
1.如图，在Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC，交AD于E，EF∥AC，下列结论一定成立的是（ ）A.AB = BFB.AE = EDC.AD = DCD.∠ABE =∠DFE
2.如图，AB = CD，AD = BC，O为BD上任意一点，过O点的直线分别交AD，BC于M、N点.求证：∠1 =∠2.
证明：在△ABD和△CDB中，∴△ABD≌△CDB（SSS）.∴∠ADB=∠CBD，∴AD∥BC，∴∠1=∠2.
3.如图，在 △ABC 中，点D是BC的中点， DE⊥AB， DF⊥AC，E、F为垂足，DE＝DF，求证： AB=AC．
证明：∵DE⊥AB，DF⊥AC，DE = DF，∵点D是BC的中点，∴BD = CD.
在Rt△BDE和Rt△CDF中，∴Rt△BDE≌△Rt△CDF(HL).∴∠B =∠C.∴AB =AC.