人教版（2024）七年级上册5.1 方程获奖教学课件ppt

这是一份人教版（2024）七年级上册5.1 方程获奖教学课件ppt，文件包含人教版七年级数学上册511从算式到方程PPTpptx、人教版七年级数学上册511从算式到方程教学设计docx、511从算式到方程导学案docx等3份课件配套教学资源，其中PPT共30页， 欢迎下载使用。

1.掌握方程、一元一次方程的定义以及解的概念，学会判断某个数值是不是一元一次方程的解.2.初步学会如何寻找问题中的等量关系，并列出方程.
问题：一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶，客车的行驶速度是70km/h，卡车的行驶速度是60km/h，客车比卡车早1h经过B地. A，B两地间的路程是多少？
(1)上述问题中涉及到了哪些量？
客车70km/h，卡车60km/h
客车比卡车早1h到达B地
客车每小时比卡车多走10km
相同的时间，客车比卡车多走60km
算式：60÷(70-60)×70=420(km)
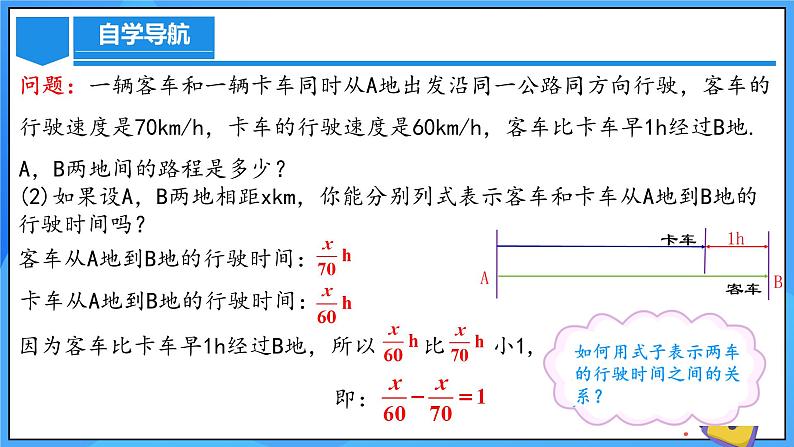
(2)如果设A，B两地相距xkm，你能分别列式表示客车和卡车从A地到B地的行驶时间吗？
客车从A地到B地的行驶时间：
卡车从A地到B地的行驶时间：
解：设客车从A地到B地的时间为xh，则卡车从A到B的所用时间为(x+1)h.由A到B的路程为定值可列方程： 70x=60(x+1)
【点睛】列方程时，要先设字母表示未知数，然后根据问题中的相等关系，写出含有未知数的等式--方程.
从算式到方程是数学的进步！
列算式:列出的算式表示解题的计算过程, 只能用已知数.对于较复杂的问题,列算式比较困难.
列方程:方程是根据题中的等量关系列出的等式. 既可用已知数,又可用未知数,解决问题比较方便.
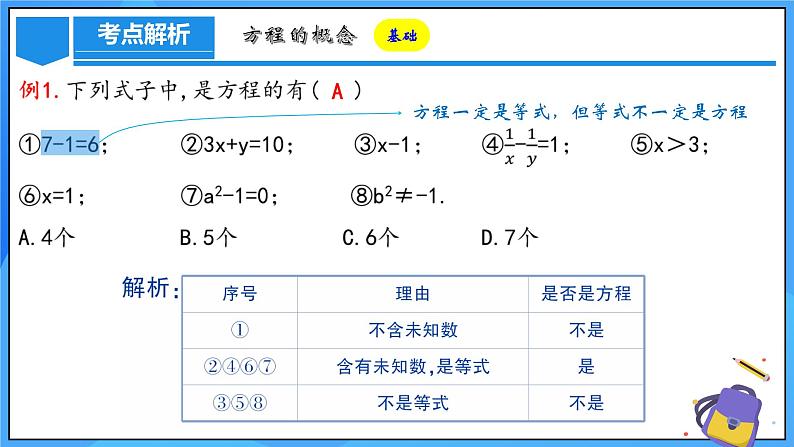
方程一定是等式，但等式不一定是方程
下列方程有什么共同特点？
一元一次方程： 上面各方程都只含有一个未知数(元)，未知数的次数都是1，等号两边都是整式，这样的方程叫做一元一次方程.
3.如果方程(m-1)x+3=0是关于x的一元一次方程，那么m的取值范围是________.4.若方程2xm+1=0是关于x的一元一次方程，则m的值为______.
根据一元一次方程的概念求字母或式子的值
例3.若(3-m)x|m|-2-8=0是关于x的一元一次方程，则m的值为( )A.-3 B.3 C.±3 D.1
表示x是未知数，m是已知数
解析:因为(3-m)x|m|-2-8=0是关于x的一元一次方程，所以|m|-2=1，且3-m≠0.由|m|-2=1，得m=3或m=-3.因为3-m≠0，所以m=3不合题意.所以m=-3.
怎样将一个实际问题转化为方程问题？
设未知数 列方程
列方程是解决问题的重要方法，利用方程可以求出未知数.  
可以发现，当x=6时，4x的值是24，
同样地，当x=5时，1700+150x的值是2450，这时方程1700+150x=2450等号左右两边相等.
这时方程4x=24等号左右两边相等.
x=6叫做方程4x=24的解.这就是说，方程4x=24中未知数x的值应是6.
x=5叫做方程1700+150x=2450的解.这就是说，方程1700+150x=2450中未知数x的值应是5.  
解方程就是求出使方程中等号左右两边相等的未知数的值，这个值就是方程的解.
x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x=80的解？
解：当x=1000时，方程左边=0.52×1000-(1-0.52)×1000=520-480=40，右边=80，左边≠右边，所以x=1000不是此方程的解.当x=2000时，方程左边=0.52×2000-(1-0.52)×2000=1040-960=80，右边=80，左边=右边，所以x=2000是此方程的解.
【点睛】判断一个数值是不是方程的解的步骤：1.将数值代入方程左边进行计算；2.将数值代入方程右边进行计算；3.若左边＝右边，则是方程的解，反之，则不是．
例4.检验下列各数是否为方程6x+1=4x-3的解:(1)x=-1；(2)x=-2.
解:(1)当x=-1时，左边=6×(-1)+1=-5，右边=4×(-1)-3=-7，因为左边≠右边，所以x=-1不是方程6x+1 =4x-3的解.(2)当x=-2时，左边=6×(-2)+1=-11，右边=4×(-2)-3=-11，因为左边=右边，所以x=-2是方程6x+1=4x-3的解.
4.检验下列各数是否为方程2x-3=5(x-3)的解:(1)x=4；(2)x=6.解:(1)当x=4时，左边=2×4-3=5，右边=5×(4-3)=5，左边=右边，所以x=4是方程2x-3=5(x-3)的解.(2)当x=6时，左边=2×6-3=9，右边=5×(6-3)=15，左边≠右边，所以x=6不是方程2x-3=5(x-3)的解.
根据方程的解的概念求字母或式子的值
1.若x=1是关于x的方程ax+b=c的解，则(a+b-c)2=______.2.方程-5x+▲=4x，“▲”处是被墨水盖住的常数，已知方程的解是x=-1，那么“▲”处的常数是______.3.若x=1是关于x的方程-2mx+n=1的解，求2025+n-2m的值.解:将x=1代入方程-2mx+n=1，得-2m+n=1，即n-2m=1，所以2025+n-2m=2025+1=2026.
例6.【建模思想】根据下列问题，设未知数，列出方程:(1)用一根长为52cm的铁丝围成一个正方形，求正方形的边长；(2)某数的一半比这个数小8，求这个数；(3)20名同学在植树节这天共种了52棵树苗，男生每人种3棵，女生每人种2棵，求男生的人数.
例7.根据下列问题，设未知数并列出方程 (新教材例题)(1)某校女生占全体学生数的52%，比男生多80人，这所学校有多少名学生?(2)如图5.1-2，一块正方形绿地沿某一方向加宽5m，扩大后的绿地面积是500m，求正方形绿地的边长.
解:(1)设这所学校的学生数为x，那么女生数为0.52x，男生数为(1-0.52)x.根据“女生比男生多 80人”，列得方程
0.52x-(1-0.52)x-80.
(2)设正方形绿地的边长为x m，那么扩大后的绿地面积为(x2+5x)m2.根据“扩大后的绿地面积是 500 m2”，列得方程
1.“某数与2的和的3倍是9”，若设该数是x，则所列方程是( )A.x+2×3=9 B.3(x+2)=9 C.3x+2=9 D.2x+3=92.用一根长为48cm的铁丝围成一个长方形，其中长方形的长为15cm，求长方形的宽.设宽为xcm，则可列方程_________________.3.某校男生占全体学生数的48%，比女生少80人，这个学校的学生总数是多少?设这个学校的学生总数为x，则可列方程为( )(1-0.48)x=80 B.(1-0.48)x-0.48x=(1+0.48)x=80 D.(1+0.48)x-0.48x=80
4.根据下列问题，设未知数，列出方程:(1)甲书每本5元，乙书每本4元，元元用70元买了两种图书共15本，求他买的甲书的本数.(2)小明和小刚从相距16.2km的两地同时相向而行，小明行走的速度为4km/h，2h后两人相遇，求小刚行走的速度.
解:(1)设他买的甲书的本数是x，则可列方程为5x+4(15-x)=70.(2)设小刚行走的速度为xkm/h，则可列方程为2(x+4)=16.2.
1. 一元一次方程的概念： 只含有一个未知数，未知数的次数是1，等号两边都是整式，这样的方程叫做一元一次方程.2. 方程的解： 使方程左右两边相等的未知数的值叫方程的解.求方程解的过程叫做解方程.