初中数学沪科版九年级上册23.2解直角三角形及其应用课前预习课件ppt

这是一份初中数学沪科版九年级上册23.2解直角三角形及其应用课前预习课件ppt，共29页。

1.(2024河南平顶山期末)已知在△ABC中,∠C=90°,∠A=α, AB=c,那么BC的长为(M9123004)(　    )A.c·cs α　　　B.c·tan αC. 　　     D.c·sin α
解析　在△ABC中,∠C=90°,∠A=α,AB=c,∴BC=AB·sin A=c· sin α.故选D.
2.(2024安徽合肥包河期末)在Rt△ABC中,已知∠ACB=90°, tan B= ,BC=3,那么AC的长等于(M9123004)(　    )A.1　　　　　　B.9　　　　    C. 　　　　    D.3 
解析　在Rt△ABC中,tan B= ,又因为tan B= ,BC=3,所以 = ,解得AC=1.故选A.
3.在Rt△ABC中,有下列条件,则可解直角三角形的是(M9123 004)(　    )A.已知BC=6,∠C=90°B.已知∠C=90°,∠A=60°,BC=5C.已知∠C=90°,∠A=∠BD.已知∠C=∠B=45°
解析　∵选项C、D缺少边的条件,A缺少锐角的条件,∴不能 解直角三角形,选项B中,由∠A的正弦函数可求出AB,再根据 直角三角形的性质可求出∠B,然后由勾股定理或∠A的正切 函数可求出AC.故选B.
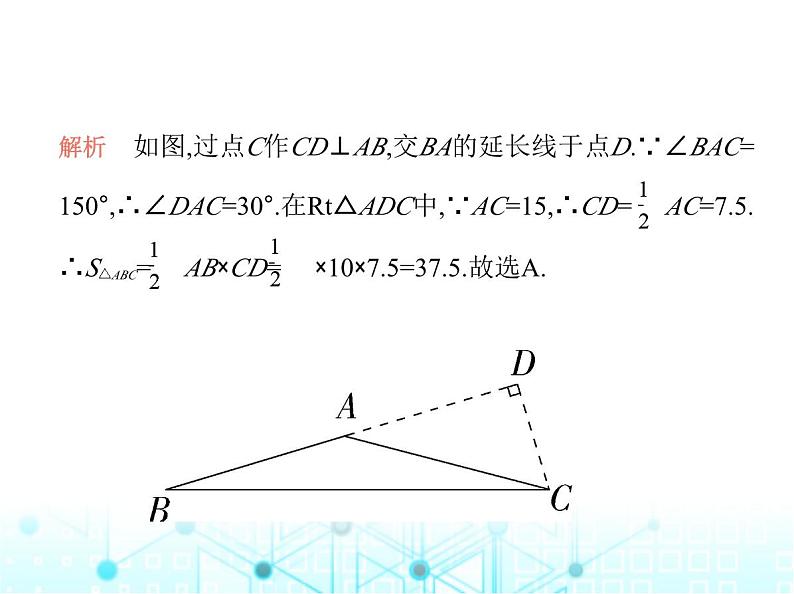
4.在△ABC中,若AB=10,AC=15,∠BAC=150°,则△ABC的面积 为 (　    )A.37.5　　　    B.75　　　    C.100　　　　　D.150
解析　如图,过点C作CD⊥AB,交BA的延长线于点D.∵∠BAC=150°,∴∠DAC=30°.在Rt△ADC中,∵AC=15,∴CD= AC=7.5.∴S△ABC= AB×CD= ×10×7.5=37.5.故选A.
5.(2023青海西宁中考)在Rt△ABC中,∠ACB=90°,AB=12,∠A =42°,则BC的长约为　　    .(结果精确到0.1.参考数据:sin 42 °≈0.67,cs 42°≈0.74,tan 42°≈0.90)
解析　∵∠ACB=90°,∴sin A= ,∵AB=12,∠A=42°,sin 42°≈0.67,∴BC=12×sin 42°≈8.0.
6.如图,在△ABC中,AD是BC边上的高,∠C=60°,AB=6 ,AC=6,则BC的长为　　　    . 
解析　在△ABC中,∵AD是BC边上的高,∴∠ADC=∠ADB= 90°.在Rt△ADC中,∵cs C=cs 60°= = ,AC=6,∴CD=3,∴AD= =3 .在Rt△ADB中,BD= = = =9,∴BC=BD+CD=9+3=12.
7.(新独家原创)如图,在△ABC中,∠B=30°,AB=8,AC=4 ,则∠C=　　　    ,BC=　　　    .
解析　如图,过A作AD⊥BC于D,则∠ADB=∠ADC=90°,∵AB =8,∠B=30°,∴AD=AB·sin 30°=8× =4,BD=AB·cs 30°=8× =4 .在Rt△ACD中,sin C= = = ,∴∠C=45°,∴CD=AD=4.∴BC=BD+CD=4 +4.
8.(教材变式·P125T2)在Rt△ABC中,∠C=90°,∠A、∠B、∠ C的对边分别是a、b、c,分别根据下列条件解直角三角形. (M9123004)(1)b=2 ,c=4;(2)∠A=30°,b=8 ;(3)c=8,∠A=45°.
解析    (1)在Rt△ABC中,∠C=90°,b=2 ,c=4,∴a= = =2.∵cs A= = = ,∴∠A=30°,∴∠B=90°-30°=60°.(2)在Rt△ABC中,∠C=90°,∠A=30°,∴∠B=90°-∠A=60°.∵ tan A= = ,b=8 ,∴ = ,∴a=8.∵sin B= = ,b=8 ,∴ = ,∴c=16.(3)在Rt△ABC中,∠C=90°,∠A=45°,∴∠B=90°-∠A=45°=∠A,∴a=b.
∵sin A= = ,c=8,∴ = ,∴a=4 ,∴b=4 .
9.(2024安徽安庆期末)如图,在△ABC中,∠C=90°,点D在AC 上,∠BDC=45°,BD=10 ,AB=20.求sin A的值.(M9123004) 
解析　在Rt△BDC中,∠BDC=45°,BD=10 ,∴BC=BD·sin∠BDC=10 × =10.在Rt△ABC中,∠C=90°,AB=20,∴sin A= = = .
10.(2024安徽亳州期末,9, )如图,在Rt△ABC中,∠C=90°,∠BAC=30°,延长CA到点D,使AD=AB,连接BD.根据此图形可 求得tan 15°的值是(M9123004)(　    )A.2- 　　　　 B.2+ 　　　    C. 　　　　    D. 
解析　设AB=AD=2x,在Rt△ABC中,∵∠BAC=30°,∠C=90°, AB=2x,∴BC= AB=x,AC= BC= x.∵AD=AB,∴∠D=∠ABD= ∠BAC=15°,∴tan D= = =2- ,即tan 15°=2- .故选A.
11.(新考法)(2023湖北武汉中考,13, )如图,将45°的∠AOB按下面的方式放置在一把刻度尺上,顶点O与尺下沿的 端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的 读数为2 cm,若按相同的方式将37°的∠AOC放置在该刻度 尺上,则OC与尺上沿的交点C在尺上的读数约是　    cm(结 果精确到0.1 cm,参考数据:sin 37°≈0.60,cs 37°≈0.80,tan 37°≈0.75).(M9123004)
解析　本题借助刻度尺考查解直角三角形的知识,题目新颖. 如图,过点B作BD⊥OA于D,过点C作CE⊥OA于E,在△BOD 中,∠BDO=90°,∠DOB=45°,∴BD=OD=CE=2 cm,在△OCE 中,∠COE=37°,∠CEO=90°,∴tan 37°= ≈0.75,∴OE≈2.7 cm,即OC与尺上沿的交点C在尺上的读数约是2.7 cm.
12.(构造直角三角形法)(2024安徽六安金安期末,17, )如图,在△ABC中,∠A=30°,∠B=45°,AC=2 ,求AB的长.(M9123004) 
解析　过C作CD⊥AB于D,如图,
∴∠ADC=∠BDC=90°,∵∠B=45°,∴∠BCD=∠B=45°,∴CD =BD,∵∠A=30°,AC=2 ,∴CD=AC·sin 30°= ,∴BD=CD=
 ,由勾股定理得,AD= =3,∴AB=AD+BD=3+ .
13.(创新意识)(新独家原创)(新考向·教材拓展探究试题)【教材呈现】下图是沪科版九年级上册数学教材第125页的 部分内容.
【得出结论】在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,则 有S△ABC= absin C= bcsin A= acsin B.【结论应用】(1)锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若a =30 cm,b=36 cm,∠C=30°,求△ABC的面积.(2)如图,△ABC中,AB=AC=3 cm,BC=4 cm,点P从点B出发,沿 线段BC以2 cm/s的速度向终点C运动,点Q从点C出发,沿着C
→A→B的方向以3 cm/s的速度向终点B运动,P,Q同时出发,设 点P运动的时间为t(s),△CPQ的面积为S(cm2).①求sin B;②求S关于t的函数关系式,并直接写出自变量t的取值范围. 
解析    (1)根据结论,得S△ABC= absin C= ×30×36× =270(cm2).(2)①过点A作AD⊥BC,垂足为D,如图.∵AB=AC=3 cm,AD⊥BC,BC=4 cm,
∴BD= BC=2 cm,在Rt△ABD中,AB=3 cm,BD=2 cm,∴AD= = =  cm,∴sin B= = .②当0∴S= CP·CQsin C= ·(4-2t)·3t× =2 t- t2=- t2+2 t.当1

相关课件

初中数学沪科版九年级上册23.2解直角三角形及其应用优质课ppt课件： 这是一份初中数学沪科版九年级上册23.2解直角三角形及其应用优质课ppt课件，共25页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，∴∠B60°等内容，欢迎下载使用。

数学九年级上册23.2解直角三角形及其应用教案配套ppt课件： 这是一份数学九年级上册23.2解直角三角形及其应用教案配套ppt课件，共31页。

沪科版九年级上册23.2解直角三角形及其应用集体备课ppt课件： 这是一份沪科版九年级上册23.2解直角三角形及其应用集体备课ppt课件，共40页。PPT课件主要包含了命题解读，考纲解读，备课资料，考点扫描，考点1，考点2，考点3，考点4，答案D，命题点等内容，欢迎下载使用。