数学九年级上册23.2解直角三角形及其应用课前预习ppt课件

这是一份数学九年级上册23.2解直角三角形及其应用课前预习ppt课件，共24页。

1.如图,下列角中为俯角的是 (　    )A.∠1　　　　    B.∠2　　　    C.∠3　　　　　  D.∠4 
解析　根据俯角的定义,首先确定水平线,水平线以下与视线 的夹角,即是俯角.故选C.
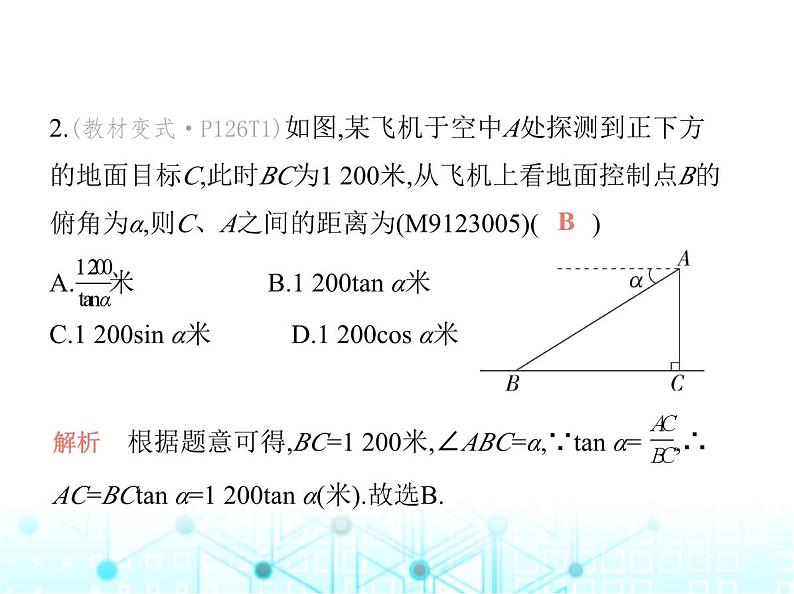
2.(教材变式·P126T1)如图,某飞机于空中A处探测到正下方 的地面目标C,此时BC为1 200米,从飞机上看地面控制点B的 俯角为α,则C、A之间的距离为(M9123005)(　    )A. 米　　     B.1 200tan α米C.1 200sin α米　　    D.1 200cs α米
解析　根据题意可得,BC=1 200米,∠ABC=α,∵tan α= ,∴AC=BCtan α=1 200tan α(米).故选B.
3.(2023湖南岳阳中考)2023年岳阳举办以“跃马江湖”为主 题的马拉松赛事.如图,某校数学兴趣小组在A处用仪器测得 赛场一宣传气球顶部E处的仰角为21.8°,仪器与气球的水平 距离BC为20米,且距地面高度AB为1.5米,则气球顶部离地面 的高度EC约是　　　　    米(结果精确到0.1米,sin 21.8°≈0. 371 4,cs 21.8°≈0.928 5,tan 21.8°≈0.400 0).
解析　由题意得,四边形ABCD是矩形,∴AB=CD=1.5 m,AD= BC=20 m,在Rt△ADE中,∵AD=BC=20 m,∠EAD=21.8°,∴DE =AD·tan 21.8°≈20×0.400 0=8(m),∴CE=CD+DE=1.5+8=9.5 (m).
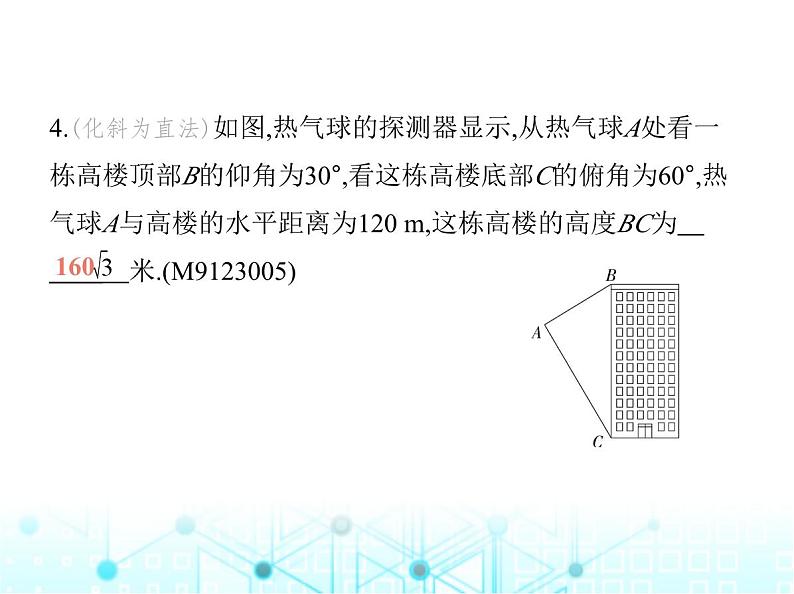
4.(化斜为直法)如图,热气球的探测器显示,从热气球A处看一 栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热 气球A与高楼的水平距离为120 m,这栋高楼的高度BC为     　　    米.(M9123005)
解析　如图,过A作AD⊥BC,垂足为D.在Rt△ABD中,∵∠ BAD=30°,AD=120 m,∴BD=AD·tan 30°=120× =40  m,在Rt△ACD中,∵∠CAD=60°,AD=120 m,∴CD=AD·tan 60°=12 0× =120  m,∴BC=BD+CD=40 +120 =160  m. 
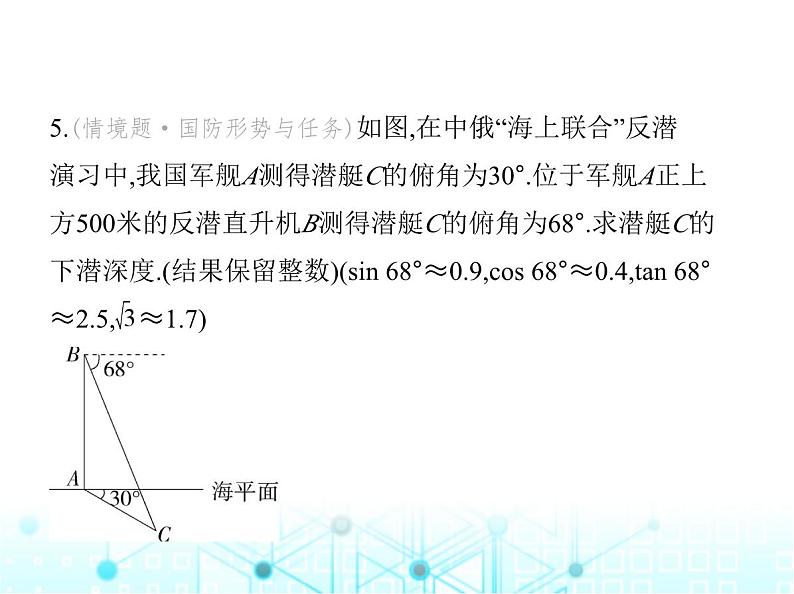
5.(情境题·国防形势与任务)如图,在中俄“海上联合”反潜 演习中,我国军舰A测得潜艇C的俯角为30°.位于军舰A正上 方500米的反潜直升机B测得潜艇C的俯角为68°.求潜艇C的 下潜深度.(结果保留整数)(sin 68°≈0.9,cs 68°≈0.4,tan 68° ≈2.5, ≈1.7) 
解析　过点C作CD⊥AB,交BA的延长线于点D(图略),则AD 为潜艇C的下潜深度,根据题意得∠ACD=30°,∠BCD=68°,设AD=x米,则BD=BA+AD=(500+x)米,在Rt△ACD中,CD= = = x(米),在Rt△BCD中,BD=CD·tan 68°= x·tan 68°(米),∴500+x= x·tan 68°,解得x= ≈ ≈154(米),
∴潜艇C的下潜深度约为154米.
6.(安徽地标建筑·骆岗公园)(2024安徽合肥蜀山期末)“时代 之舞,梦想领航”,合肥骆岗中央公园全向信标台成为合肥新 地标.小丽同学想要通过测量及计算了解信标台CD的大致 高度,如图,当她步行至点A处时,测得此时台顶C的仰角为45 °,再前进20米至点B处,测得此时台顶C的仰角为56°(点A,B,D 在同一条直线上),请帮小丽计算信标台CD的高度.(参考数 据:sin 56°≈0.83,cs 56°≈0.56,tan 56°≈1.5)(M9123005)
解析　由题意得,AB=20米,AD⊥CD.设BD=x米,∴AD=AB+BD=(x+20)米.在Rt△ACD中,∠CAD=45°,∴CD=AD·tan 45°=(x+20)米.在Rt△CBD中,∠CBD=56°,∴CD=BD·tan 56°≈1.5x(米),∴1.5x=x+20,解得x=40,∴CD=1.5x=60(米),∴信标台CD的高度约为60米.
7.(情境题·国防教育)(2023湖南永州中考,23, )永州市道县陈树湘纪念馆中陈列的陈树湘雕像高2.9米(如图1所示), 寓意陈树湘为中国革命“断肠明志”牺牲时的年龄为29岁. 如图2,以线段AB代表陈树湘雕像,一参观者在水平地面BN上 D处为陈树湘雕像拍照,相机支架CD高0.9米,在相机C处观测 雕像顶端A的仰角为45°,然后将相机支架移到MN处拍照,在 相机M处观测雕像顶端A的仰角为30°,求D、N两点间的距离 (结果精确到0.1米,参考数据: ≈1.732).(M9123005)
解析　由题意得,AB⊥BN,AH⊥HM,BH=CD=MN=0.9米,AB= 2.9米,CM=DN,∴AH=AB-BH=2.9-0.9=2(米),在Rt△AHC中,∠ACH=45°,∴CH=AH=2(米).在Rt△AHM中,∠AMH=30°,∴HM= = =2 (米),∴CM=HM-HC=2 -2≈1.5(米),∴DN=CM=1.5米,∴D、N两点间的距离约为1.5米.
8.(构造直角三角形法)(2024安徽合肥四十二中期末,19, )某建筑的截面如图所示,背面AB的倾斜角为76.1°,大门CD高6米,大门底端D点距背面点B的距离BD=30米,在大门顶 端C点测得背面顶端A的仰角为31.1°,求背面顶端A距地面的 高度.(结果保留整数,参考数据:sin 76.1°≈0.97,tan 76.1°≈4.0,sin 31.1°≈0.52,tan 31.1°≈0.60)(M9123005)
解析　如图,过A作AH⊥DB于H,过C作CN⊥AH于N,过B作 BM⊥CN于M,设AN=x米,∵CD⊥DB,
∴四边形CDHN是矩形,∴HN=CD=6米,CN=DH,∴AH=(x+6)米,∵tan∠ABH=tan 76.1°= = ≈4.0,∴BH≈ (米),∴DH=BD+BH= 米,∴CN=DH= 米,
∵tan∠ACN=tan 31.1°= ≈0.60,∴x≈ ×0.60,∴x≈22.2,∴AN≈22.2米,∴AH=AN+NH=22.2+6≈28(米),∴背面顶端A距地面的高度约是28米.
9.(创新意识)(2024上海长宁期末)小明为测量河对岸大楼的 高度,利用量角器和铅锤自制了一个简易测角器,如图1所示.测量方法:如图2,人眼在P点观察所测物体最高点C,量角器零 刻度线上A、B两点均在视线PC上,将铅锤悬挂在量角器的 中心点O.当铅锤静止时,测得视线PC与铅垂线OD所夹的角 为α,且此时的仰角为β.实践操作:如图3,小明利用上述工具测量河对岸垂直于水平 地面的大楼EF的高度.他先站在水平地面的点H处,视线为
GE,此时测角器上视线与铅垂线的夹角为60°;然后他向前走10米靠近大楼站在水平地面的点R处,视线为QE,此时测角器 上视线与铅垂线的夹角为45°.问题解决:(1)请用含α的代数式表示仰角β;(2)如果GH、QR、EF在同一平面内,小明的眼睛到水平地面 的距离为1.6米,求大楼EF的高度.(结果保留根号)
图1 图2     图3
解析    (1)如图,延长OD交PK于L,由题意得,OL⊥PK,∴∠OLP=90°,∵∠POD=α,∴∠OPL=90°-∠POD=90°-α,∴β =90°-α. (2)如图,延长GQ交EF于点M,
由题意得GM⊥EF,GH=QR=MF=1.6米,GQ=HR=10米,设EM=x米,