初中数学沪科版九年级上册23.2解直角三角形及其应用课文配套ppt课件

这是一份初中数学沪科版九年级上册23.2解直角三角形及其应用课文配套ppt课件，共23页。

1.(2023广东广州中考)如图,海中有一小岛A,在B点测得小岛 A在北偏东30°方向上,渔船从B点出发由西向东航行10海里 到达C点,在C点测得小岛A恰好在正北方向上,此时渔船与小 岛A的距离为(M9123005)(　    )A. 海里　　    B. 海里C.20海里　　     D.10 海里
解析　连接AC,图略,由题意得AC⊥CB,在Rt△ACB中,∠ABC =90°-30°=60°,BC=10海里,∴AC=BC·tan 60°=10 (海里),∴此时渔船与小岛A的距离为10 海里,故选D.
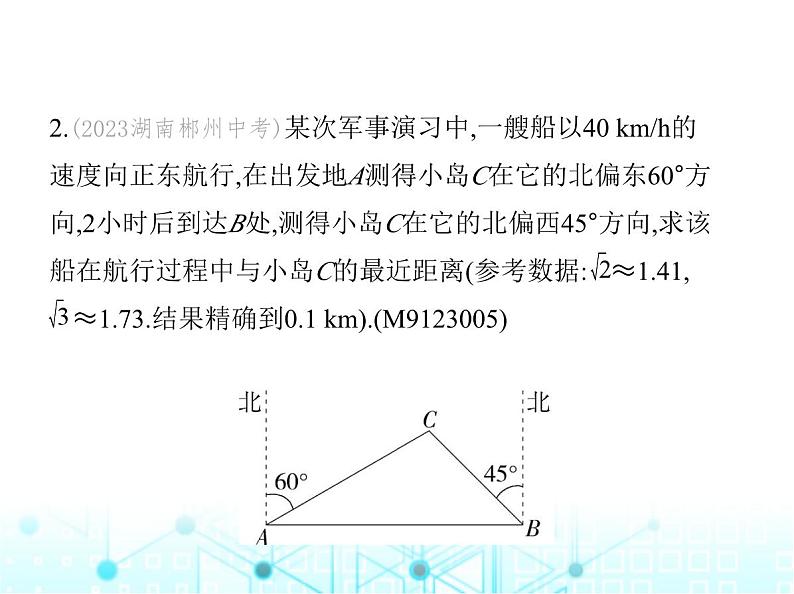
2.(2023湖南郴州中考)某次军事演习中,一艘船以40 km/h的 速度向正东航行,在出发地A测得小岛C在它的北偏东60°方 向,2小时后到达B处,测得小岛C在它的北偏西45°方向,求该 船在航行过程中与小岛C的最近距离(参考数据: ≈1.41, ≈1.73.结果精确到0.1 km).(M9123005) 
解析　由题意,得AB=40×2=80(km),∠CAB=30°,∠ABC=45°,如图,过C作CD⊥AB于D,
∴∠ADC=∠BDC=90°,∴AD= = CD,BD=CD,∵AB=80 km,∴ CD+CD=80,
解得CD=40 -40≈29.2(km).答:该船在航行过程中与小岛C的最近距离约为29.2 km.
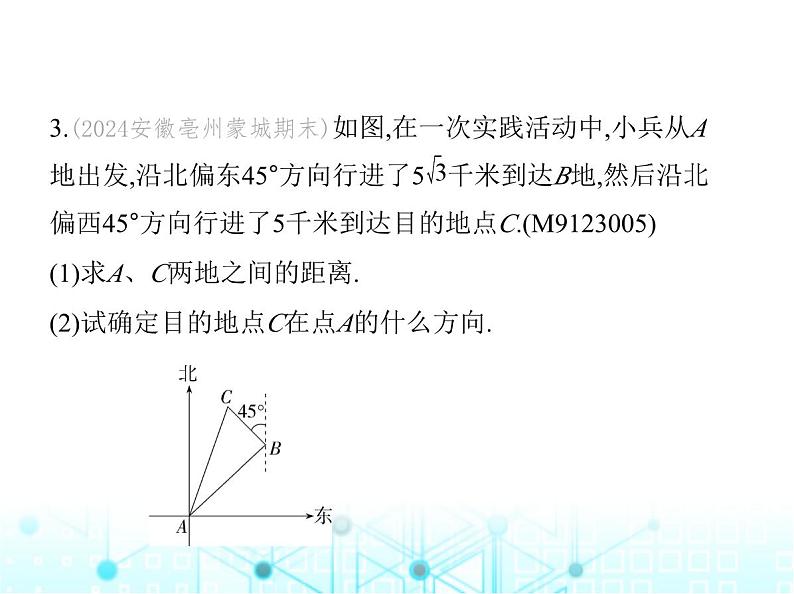
3.(2024安徽亳州蒙城期末)如图,在一次实践活动中,小兵从A 地出发,沿北偏东45°方向行进了5 千米到达B地,然后沿北偏西45°方向行进了5千米到达目的地点C.(M9123005)(1)求A、C两地之间的距离.(2)试确定目的地点C在点A的什么方向. 
解析    (1)如图,∵∠BAD=45°,∴∠ABD=45°.∴∠ABC=180°-45°-45°=90°.∴△ABC为直角 三角形.在Rt△ABC中,AC2=AB2+BC2=(5 )2+52=100,∴AC=10(千米).(2)直角三角形ABC中,tan∠CAB=BC∶AB=1∶ ,∴∠CAB=30°.∵B地在A地的北偏东45°方向上,∴目的地点C在点A的北偏 东15°方向.
4.(教材变式·P127例5)(情境题·国家安全)为了维护国家主权 和海洋权益,海监部门对我国领海进行常态化巡航.如图所 示,正在执行巡航任务的海监船以每小时60海里的速度向正 东方向航行,在A处测得灯塔P在北偏东60°方向上,继续航行 30分钟后到达B处,此时测得灯塔P在北偏东45°方向上.(M91 23005)(1)AB=　　    海里,∠APB=　　    度.(2)已知在灯塔P的周围35海里内有暗礁,问海监船继续向正 东方向航行是否安全?请说明理由.(参考数据: ≈1.41, ≈1.73)
解析    (1)AB=60× =30(海里).由题意得∠PAB=90°-60°=30°,∠ABP=90°+45°=135°,∴∠APB=180°-∠PAB-∠ABP=180°-30°-135°=15°.(2)海监船继续向正东方向航行是安全的,理由如下:过P作PH⊥直线AB于H,如图:
 易得△PBH是等腰直角三角形,∴BH=PH,设BH=PH=x海里,在Rt△APH中,tan∠PAB=tan 30°= = ,即 = ,解得x=15 +15≈40.95>35,
∴海监船继续向正东方向航行是安全的.
5.(2022安徽中考,20, )如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均 在C的北偏东37°方向上,沿正东方向行走90米至观测点D,测 得A在D的正北方向,B在D的北偏西53°方向上.求A,B两点间 的距离.(参考数据:sin 37°≈0.60,cs 37°≈0.80,tan 37°≈0.75) 
解析　如图, ∵CE∥AD,∴∠A=∠ECA=37°,∴∠CBD=∠A+∠ADB=37°+ 53°=90°,∴∠ABD=90°,易知∠BDC=90°-53°=37°,在Rt△BCD中,CD=90米,cs∠BDC = ,∴BD=CD·cs 37°≈90×0.80=72(米),
在Rt△ABD中,∠A=37°,BD=72米,tan A= ,∴AB= ≈ =96(米).答:A,B两点间的距离约为96米.
6.(2023内蒙古巴彦淖尔中考,20, )为了增强学生体质、锤炼学生意志,某校组织了一次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为B点和C点,行进路线为A→B→C→A.B点在A点的南偏东25°方向3  km处,C点在A点的北偏东80°方向,行进路线AB和BC所在直线的夹角∠ABC为45°.(M9123005)(1)求行进路线BC和CA所在直线的夹角∠BCA的度数;(2)求检查点B和C之间的距离(结果保留根号).
解析    (1)由题意得∠NAC=80°,∠BAS=25°,∴∠CAB=180°-∠NAC-∠BAS=75°.∵∠ABC=45°,∴∠ACB=180°-∠CAB-∠ABC=60°,∴行进路线BC和CA所在直线的夹角∠BCA的度数为60°.(2)过点A作AD⊥BC,垂足为D,如图,
在Rt△ABD中,AB=3  km,∠ABC=45°,∴AD=AB·sin 45°=3 × =3(km),BD=AB·cs 45°=3 × =3(km),在Rt△ADC中,∠ACB=60°,∴CD= = = (km),∴BC=BD+CD=(3+ )km,∴检查点B和C之间的距离为(3+ )km.
7.(应用意识)(情境题·劳动生产)(2024重庆巴蜀中学期末)某 校同学们积极参加劳动实践,在校园“耕读园”里播种了近 百粒萝卜种子.某周日下午返校时涵涵和静静约好一起去 “耕读园”看看萝卜的生长情况.如图,已知“耕读园”在点 A处,涵涵家位于点A正南方一条东西走向的街道BD上,且在 “耕读园”西南方向800米的C处;静静家位于点D正北方向 100 米且位于“耕读园”南偏西60°方向上的点E处,图中点A、B、C、D、E在同一平面内.(M9123005)(1)求静静家离“耕读园”的距离.(结果保留根号)
(2)涵涵周日下午5:40出门,先以80米/分钟的速度从C出发,往 正西方向走到点D处后再向正北方向走到静静家楼下,两人 碰面,然后两人以此速度沿路线EA一起前往“耕读园”,请 问她们能在5:55前到达“耕读园”吗?(参考数据: ≈1.414, ≈2.449,结果精确到十分位) 
解析    (1)如图,过E作EH⊥AB于H,则∠EHA=∠BHE=90°.∵△ABC中,∠B=90°,∠BAC=45°,∴∠ACB=90°-∠BAC=45°=∠BAC,∴BA=BC.在Rt△ABC中,由勾股定理,得AC2=AB2+BC2.∵AC=800米,∴AB=BC=400 米.∵∠D=∠B=∠BHE=90°,
∴四边形EDBH为矩形,∴HE=BD,ED=HB.∵ED=100 米,∴ED=HB=100 米,∴AH=AB-HB=300 米.∵∠AHE=90°,∠EAH=60°,∴AE= = =600 (米).答:静静家离“耕读园”的距离为600 米.(2)如图,∵∠AHE=90°,∠EAH=60°,AE=600 米,