沪科版初中九年级数学上册专项素养综合练(四)相似三角形五种辅助线的作法课件

这是一份沪科版初中九年级数学上册专项素养综合练(四)相似三角形五种辅助线的作法课件，共29页。
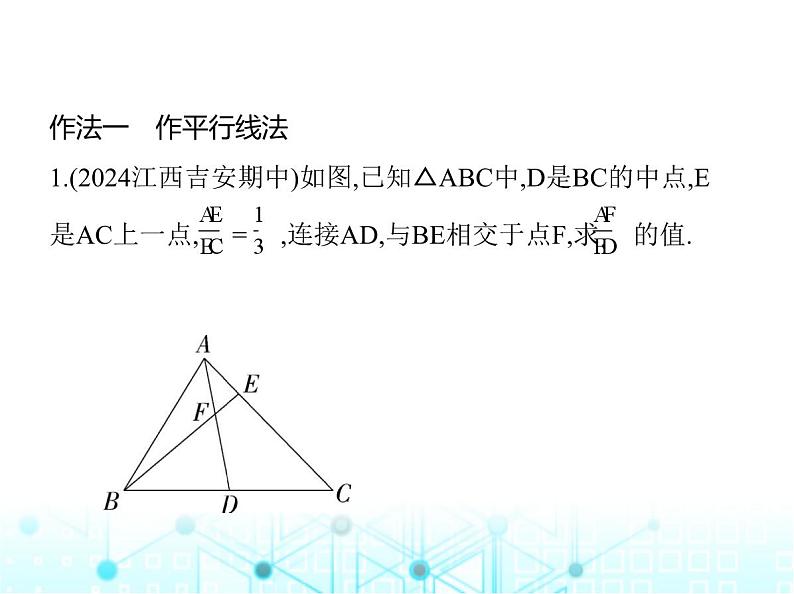
作法一　作平行线法1.(2024江西吉安期中)如图,已知△ABC中,D是BC的中点,E 是AC上一点, = ,连接AD,与BE相交于点F,求 的值. 
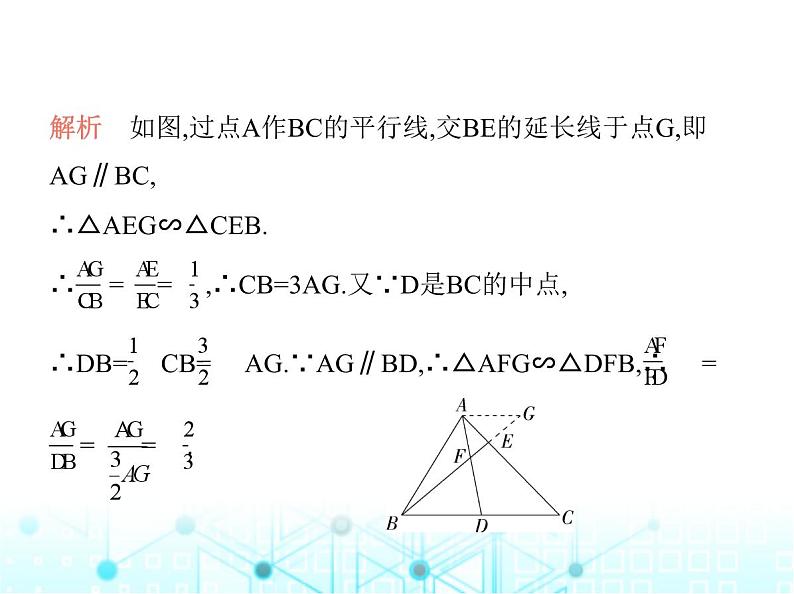
∴DB= CB= AG.∵AG∥BD,∴△AFG∽△DFB,∴ = = = .
解析　如图,过点A作BC的平行线,交BE的延长线于点G,即 AG∥BC,∴△AEG∽△CEB.∴ = = ,∴CB=3AG.又∵D是BC的中点,
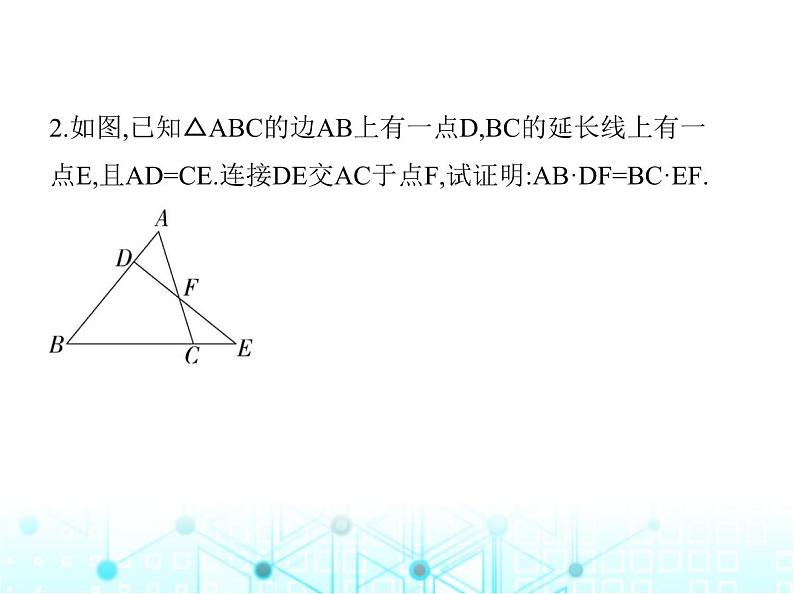
2.如图,已知△ABC的边AB上有一点D,BC的延长线上有一 点E,且AD=CE.连接DE交AC于点F,试证明:AB·DF=BC·EF. 
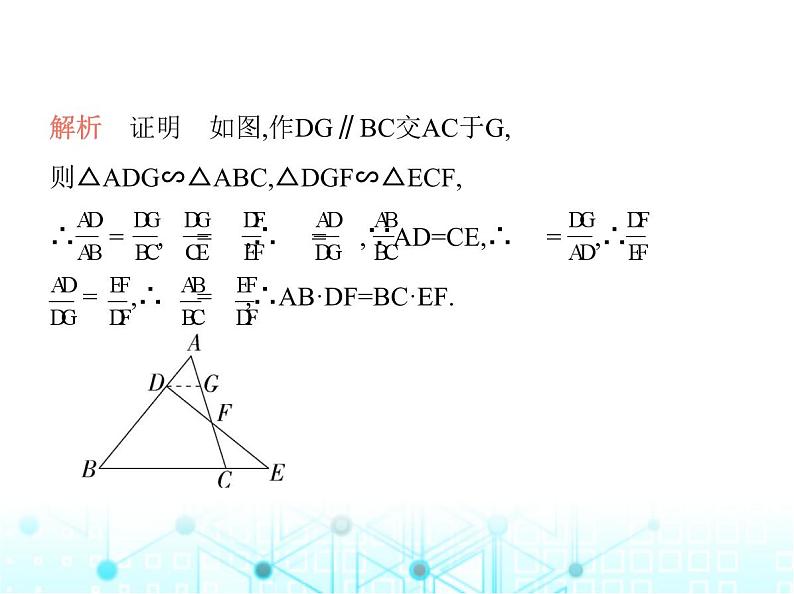
解析    证明　如图,作DG∥BC交AC于G,则△ADG∽△ABC,△DGF∽△ECF,∴ = , = ,∴ = ,∵AD=CE,∴ = ,∴ = ,∴ = ,∴AB·DF=BC·EF. 
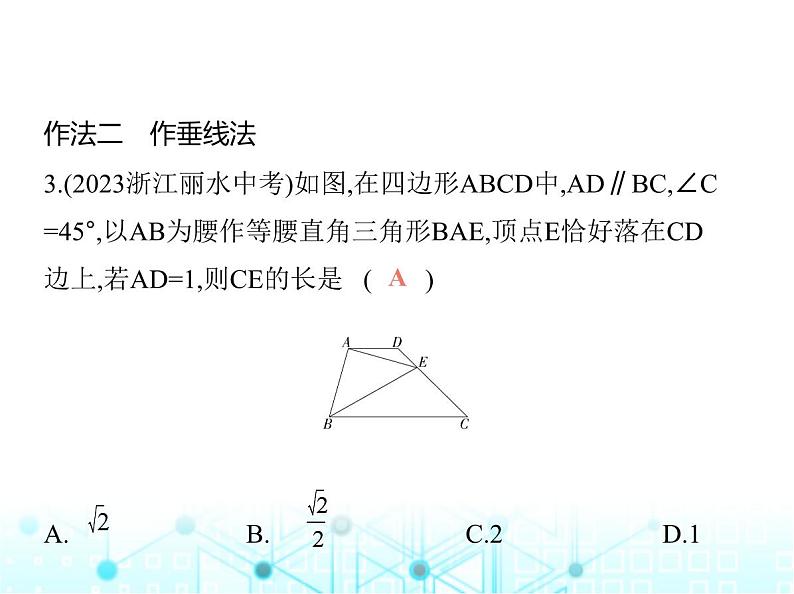
作法二　作垂线法3.(2023浙江丽水中考)如图,在四边形ABCD中,AD∥BC,∠C =45°,以AB为腰作等腰直角三角形BAE,顶点E恰好落在CD 边上,若AD=1,则CE的长是 (　    ) A. 　　　　　　B. 　　　　　　C.2　　　　　　D.1
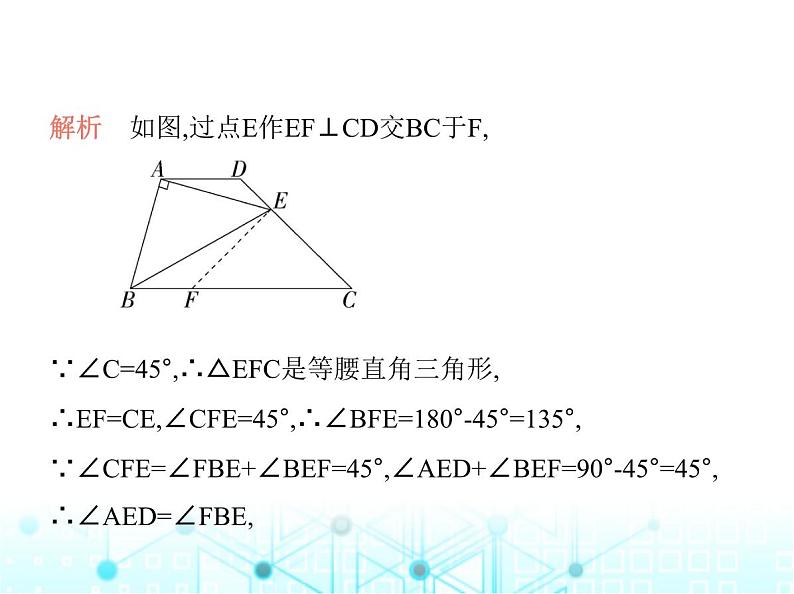
解析　如图,过点E作EF⊥CD交BC于F, ∵∠C=45°,∴△EFC是等腰直角三角形,∴EF=CE,∠CFE=45°,∴∠BFE=180°-45°=135°,∵∠CFE=∠FBE+∠BEF=45°,∠AED+∠BEF=90°-45°=45°, ∴∠AED=∠FBE,
∵△ABE是等腰直角三角形,∴ = ,∵AD∥BC,∴∠C+∠D=180°,∴∠D=180°-45°=135°,∴∠D=∠BFE,∴△ADE∽△EFB,∴ = = ,∵AD=1,∴EF= ,∴CE=EF= .
4.如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,点F在 边BC上,且BF=2FC,AF分别与DE,DB相交于点M,N,求MN的 长. 
解析　如图,过点F作FH⊥AD于点H,交ED于点O,∴FH=AB= 2.∵BF=2FC,BC=AD=3,∴BF=AH=2,FC=HD=1,∴AF= = =2 .∵AB=2,E为AB的中点,∴AE=1,∵BA⊥AD,FH⊥AD,∴OH∥AE,∴ = = ,∴OH= AE= ,∴OF=FH-OH=2- = .
= .∵AD∥BF,∴△AND∽△FNB,∴ = = ,∴AN= AF= ,∴MN=AN-AM= - = .
∵AE∥FO,∴△AME∽△FMO,∴ = = = ,∴AM= AF
5.如图,在△ABC中,∠C=90°,D为AB的中点,点M为射线AC 上一点,点N为射线CB上一点,且DM⊥DN.(1)求证: = .(2)若BC=6,AC=8,CM=5,求CN的长. 
∴∠MQD=∠DPN=90°.∵∠C=90°,∴四边形DPCQ是矩形,∴∠QDP=90°,DQ∥BC,DP∥QC,∵DM⊥DN,∴∠MDQ+∠QDN=∠QDN+∠NDP=90°,∴∠MDQ=∠NDP,∴△DMQ∽△DNP,∴ = ,∵DQ∥BC,DP∥QC,D为AB的中点,∴DQ= 
解析    (1)证明:如图,过D作DP⊥BC于P,DQ⊥AC于Q,
BC,DP= AC,∴ = .(2)如图,∵AC=8,∴AQ=CQ=4,∵CM=5,∴MQ=MC-CQ=5-4= 1,∵DQ= BC=3,DP= AC=4,△DMQ∽△DNP,∴ = = ,∴NP= .∵CP=BP=3,
作法三　延长线法6.如图,在正方形ABCD中,M为AD中点,以M为顶点作∠ BMN=∠MBC,MN交CD于N,求证:DN=2NC. 
解析    证明　如图,连接MC,延长MN、BC交于点E.设AB=2a,则AM=a,BM= a.∵AB=CD,∠A=∠D=90°,AM=MD,∴△BAM≌△CDM,∴ BM=MC,∴∠BCM=∠CBM=∠BMN,∴△BMC∽△BEM,∴ = ,即 = ,∴BE= a,∴CE=BE-BC= a-2a= a.∵四边形ABCD为正方形,
∴∠D=∠DCB=90°,即∠D=∠NCE=90°.∵∠DNM=∠CNE, ∴△MDN∽△ECN,∴ = = =2,即DN=2NC.
7.如图,在四边形ABCD中,AD∥BC,若∠BCD的平分线CE⊥ AB于点E,BE=2AE,且四边形AECD的面积为21,求△EBC的 面积. 
解析　延长BA、CD交于点F,过点D作DM⊥AF于点M,如图 所示.∵∠BCD的平分线CE⊥AB于点E,∴BC=CF,∴∠B=∠F,BE=EF.∵AD∥BC,∴∠FAD=∠B,∴∠FAD=∠F,∴DA=DF.
∵DM⊥AF,∴FM= AF.∵BE=EF,BE=2AE,∴2AE=EF,∴AF=AE,∴FM= AF= FE.∵DM⊥AF,CE⊥AB,∴DM∥CE,∴ = = ,∴DM= CE.∵ =S△CEF-S△DAF= EF·CE- AF·DM= EF·CE- EF·
CE=21,∴EF·CE=48,∴S△EBC=S△CEF= EF·CE=24.
作法四　作中线、中位线法8.如图,把两个相同的含30°角的直角三角板按如图所示的方 式拼接在一起,点N是AB边的中点,连接DN交BC于点M,求  的值. 
解析　连接CN,如图,设AC=2a.∵∠ABC=30°,∠ACB=90°,∴AB=4a,BC=2 a.∵点N是AB边的中点,∴CN=AN=BN= AB=2a.∵∠DBC=30°,∠CDB=90°,∴CD= BC= a,∴BD= =3a.∵NC=NB,∴∠NCB=∠ABC=30°.∵∠BCD=60°,∴∠NCD=∠NCB+∠BCD=90°,∴∠NCD+∠BDC=90°+90°=180°,
∴NC∥BD,∴△MCN∽△MBD,∴ = = = ,∴ = .
9.如图,在△ABC中,D,E分别是边BC,AB的中点,AD,CE相交 于点G,求证: = = . 
解析    证明　连接ED,图略.∵在△ABC中,D,E分别是边BC,AB的中点,∴DE是△ABC的中位线,∴DE∥AC,DE= AC,∴△ACG∽△DEG,∴ = = =2,∴ = =3,∴ = = .
作法五　巧连线段法10.(2024上海虹口期中)已知,在菱形ABCD中,CE⊥AB,垂足 为E,CE与BD相交于点F.(1)求证: = ;(2)求证:DF·DB=2BC2. 
解析    证明    (1)∵四边形ABCD是菱形,∴DC∥AB,DC=AB,∴DC∥BE,∴△DCF∽△BEF,∴ = ,∴ = .(2)如图,连接AC交BD于点H,则AC⊥BD,∴∠DHC=90°.∵CE⊥AB,垂足为E,DC∥AB,∴∠DCE=∠ BEC=90°,∴∠DHC=∠DCF.∵∠HDC=∠CDF,