北师大版初中九年级数学上册期末素养综合测试(一)课件

这是一份北师大版初中九年级数学上册期末素养综合测试(一)课件，共54页。

一、选择题(本大题共10小题,每小题3分,共30分)
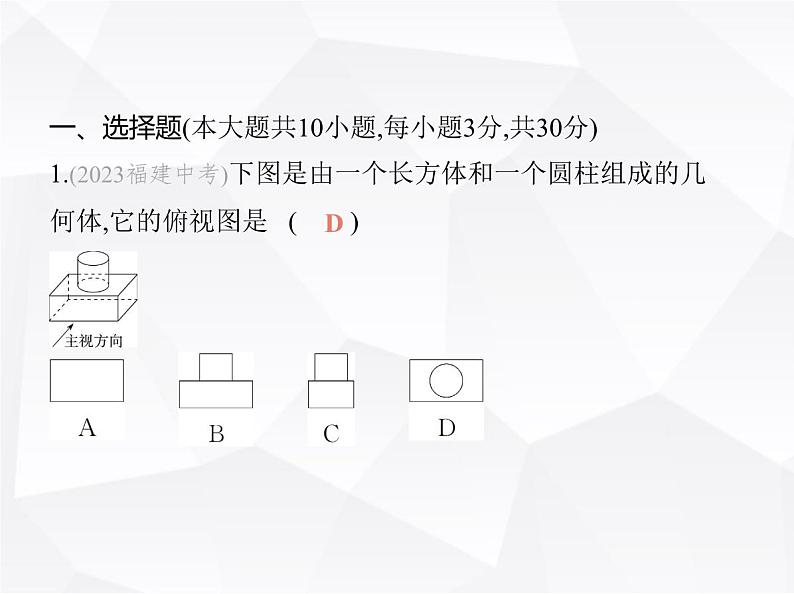
1.(2023福建中考)下图是由一个长方体和一个圆柱组成的几 何体,它的俯视图是 (　    )  　     　     　     
解析　∵关于x的一元二次方程(a-1)x2-2x+a2-1=0有一个根为 x=0,∴a2-1=0且a-1≠0,则a的值为-1.故选D.
2.(2023河北保定竞秀期中)已知关于x的一元二次方程(a-1)x2-2x+a2-1=0有一个根为x=0，则a的值为 (　    )A.0B. ±1C.1D.-1
3.(2023云南中考)若点A(1,3)是反比例函数y= (k≠0)图象上一点,则常数k的值为 (　    )A.3　　　    B.-3　　　    C. 　　　    D.- 
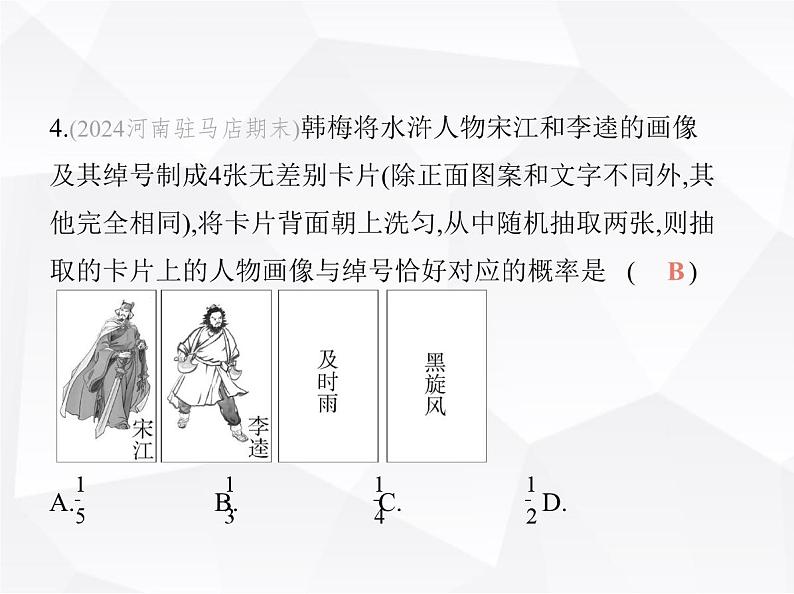
4.(2024河南驻马店期末)韩梅将水浒人物宋江和李逵的画像 及其绰号制成4张无差别卡片(除正面图案和文字不同外,其 他完全相同),将卡片背面朝上洗匀,从中随机抽取两张,则抽 取的卡片上的人物画像与绰号恰好对应的概率是 (　    )
A. 　　　    B. 　　　    C. 　　　    D. 
解析　将宋江、李逵、及时雨、黑旋风分别用A、B、C、D 表示,画树状图如图所示:共有12种等可能的结果,其中抽取的卡片上的人物画像与绰 号恰好对应的结果有4种,
∴抽取的卡片上的人物画像与绰号恰好对应的概率为 = ,故选B.
5.(2024河南安阳期末)如图,l1∥l2∥l3,若AB=2,BC=3,则 的值为 (　    )A. 　　　    B. 　　　    C. 　　　    D. 
6.(2024河南叶县期末)如图,在平行四边形ABCD中,E、F是 对角线AC上的两点(不与点A、C重合),且AE=CF,分别连接 BE、BF、DE、DF,则下列结论错误的是 (　    )A.四边形BFDE是平行四边形B.若四边形ABCD是菱形,那么四边形BFDE也是菱形
C.若四边形ABCD是正方形,那么四边形BFDE是菱形D.若四边形ABCD是矩形,那么四边形BFDE也是矩形
解析　连接BD交AC于点O,如图所示: ∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵AE=CF, ∴OE=OF,∴四边形BFDE是平行四边形,故A不符合题意;当四边形ABCD是菱形时,BD⊥AC,∴EF⊥BD,∵四边形 BFDE是平行四边形,∴四边形BFDE是菱形,故B不符合题意;
当四边形ABCD是正方形时,BD⊥AC,∴EF⊥BD,∵四边形 BFDE是平行四边形,∴四边形BFDE是菱形,故C不符合题意;当四边形ABCD是矩形时,AC=BD,∵EF≠BD,∴四边形 BFDE不是矩形,故D符合题意.
7.(跨学科·物理)(2024山东莘县期末)在物理学中,功率表示做 功的快慢,功与做功时间的比叫做功率,即所做的功一定时, 功率P(W)与做功所用的时间t(s)成反比例函数关系,图象如 图所示,下列说法不正确的是 (　    )
A.P与t的函数关系式为P= B.当t=5 s时,P=12 000 WC.当t>5 s时,P>12 000 WD.P随t的增大而减小
解析　设P与t的函数解析式为P= (k≠0),把(15,4 000)代入解析式得4 000= ,解得k=60 000,∴P与t的函数解析式为P= ,故A不符合题意;当t=5 s时,P= =12 000 W,故B不符合题意;当t>5 s时,P<12 000 W,故C符合题意;∵60 000>0,∴在第一象限内,P随t的增大而减小,故D不符合 题意.故选C.
8.(2023福建南平期中)生物兴趣小组的学生将自己收集的标 本向本组其他成员各赠送一件,全组共互赠了182件,那么该 组共有学生(　    )A.12名　　　    B.13名　　　    C.14名　　　    D.15名
解析　设全组有x名学生,则每名学生所赠送的标本为(x-1) 件,那么x名学生共赠送x(x-1)件,则x(x-1)=182,整理得x2-x-182 =0,解得x1=-13(不合题意,舍去),x2=14.故该组共有14名学生. 故选C.
9.(2023河北邯郸大名一中期末)如图,小明在A时测得某树的 影长为3 m,B时又测得该树的影长为2 m.若两次日照的光线 互相垂直,则树的高度为 (　    ) A.  m　　　    B.2  m　　　    C.6 m　　　    D.  m
解析　如图: ∵∠CEF+∠CFE=90°,∠CEF+∠ECD=90°,∴∠ECD=∠CFE,又∵∠EDC=∠CDF=90°,∴△EDC∽△CDF,∴ = ,即DC2=ED·FD=2×3=6,解得CD=  m.故选A.
10.(2023四川成都武侯一诊)如图,已知直线l是线段AB的垂 直平分线,l与AB相交于点C,点D是位于直线AB下方的l上的 一动点,连接AD,BD.过点A作AE∥BD,过点B作BE⊥AE,AE与 BE相交于点E.若AB=6,设AD=x,AE=y,则y关于x的函数关系用 图象可以大致表示为 (　    )
解析　∵直线l是线段AB的垂直平分线,∴CD⊥AB,DB=AD=x,AC=BC= AB=3,∵AE∥BD,∴∠BAE=∠ABD,又∵∠E=∠BCD=90°,∴△AEB∽△BCD,∴ = ,∴ = ,∴y= ,∵点D是位于直线AB下方的l上的一动点,∴x>3,只有B选项 符合题意.故选B.
二、填空题(本大题共8小题,每小题3分,共24分)
11.(2024河南邓州期末)请在横线上填写一个恰当的整数,使 方程2x2-5x+　　 　    =0有两个不相等的实数根.
12.(一题多解)(2024江苏沭阳期末)若 = ,则 =　　        .
13.(2023天津津南期末)一名球员练习投篮的结果记录如表:
先将表中数据补全(精确到0.01);再根据以上数据估计,这名 球员投篮一次,投中的概率是　　 　    .(精确到0.1)
0.49;0.51;0.5
解析    123÷250≈0.49,152÷300≈0.51.根据补全的表格估计,这名球员投篮一次,投中的概率是0.5.
14.(情境题·现实生活)(2022湖南娄底中考)九年级融融陪同 父母选购家装木地板,她感觉某品牌木地板拼接图(如实物 图)比较美观,通过手绘(如图)、测量、计算发现点E是AD的 黄金分割点,即DE≈0.618AD,延长HF与AD相交于点G,则EG ≈　　　    DE.(精确到0.001)
解析　∵点E是AD的黄金分割点,即DE≈0.618AD,∴ = ≈0.618,由题意得EG=AE,∴ ≈0.618,∴EG≈0.618DE,故答案为0.618.
15.(2023山东青岛月考)出门即公园,入眼皆美景.近年来随着 “口袋公园”的相继建设,市民的幸福感在不断提升.如图, 在某口袋公园内有一块长16 m,宽9 m的矩形小广场,中间建 造了一个面积为小广场面积一半的喷泉景观,已知喷泉四周 小路的宽度都相等.若设小路的宽度为x m,则列出的方程为 　 　　    .
解析　∵小路的宽度为x m,∴矩形喷泉景观的长为(16-2x)m,宽为(9-2x)m.根据题意得(16-2x)(9-2x)= ×16×9.
16.(2024山西大同期末)某几何体的三视图如图所示,根据图 中提供的数据可知,该几何体的体积为　　　    cm3. 
解析　由三视图可确定该几何体是圆柱,底面圆的半径是2÷ 2=1(cm),高是2 cm,所以该几何体的体积为π×12×2=2π(cm3).故答案为2π.
17.(2023山东青岛市南期中)如图,在△ABC中,中线BE、CD 相交于点O,连接DE,下列结论:① = ;② = ;③ = ;④ = .其中正确的有　　　    (写序号). 
解析　∵BE、CD是△ABC的中线,∴D、E是AB和AC的中点,∴DE是△ABC的中位线,∴DE∥BC,DE= BC,∴△DOE∽△COB,△ADE∽△ABC,∴ = = = = ,∴ = = ,故①正确,②错误,③正确;
设S△DOE=x,∵ = ,∴S△EOC=2x,∴S△DEC=S△DOE+S△EOC=3x,∵E是AC的中点,∴S△ADE=S△DEC=3x,∴S△ADC=S△ADE+S△DEC=6x,∴ = = ,故④正确.故答案为①③④.
18.(2022贵州黔东南州中考)如图,折叠边长为4 cm的正方形 纸片ABCD,折痕是DM,点C落在点E处,分别延长ME、DE交 AB于点F、G,若点M是BC边的中点,则FG=　　　    cm. 
解析　如图,连接DF,∵四边形ABCD是正方形,∴AD=CD=AB=BC=4 cm,∠A=∠B=∠C=90°,∵点 M是BC边的中点,∴CM=BM= BC=2 cm,由折叠得DE=CD=4 cm,EM=CM=2 cm,∠DEM=∠C=90°,∴∠DEF=180°-90°=90°,AD=DE,∴∠A=∠DEF,在Rt△DAF和Rt△DEF中, ∴Rt△DAF≌Rt△DEF(HL),∴AF=EF,
设AF=x cm,则EF=x cm,BF=(4-x)cm,∴FM=(x+2)cm,在Rt△BFM中,BF2+BM2=FM2,∴(4-x)2+22=(x+2)2,解得x= ,∴AF=EF=  cm,BF=4- = (cm),FM= +2= (cm),∵∠FEG=∠DEM=90°,∴∠FEG=∠B,又∵∠EFG=∠BFM,∴△FGE∽△FMB,∴ = ,即 = ,
∴FG=  cm,故答案为 . 
三、解答题(共66分)
19.[答案含评分细则](2024河南郑州一中教育集团紫荆中学 月考)(10分)解下列方程:(1)2x(x+1)=x+1.(2)(x+3)(x+7)=-2.
解析    (1)∵2x(x+1)=x+1,∴2x(x+1)-(x+1)=0, 1分∴(x+1)(2x-1)=0, 2分∴x+1=0或2x-1=0, 3分解得x1=-1,x2=0.5. 5分(2)整理,得x2+10x+23=0, 6分∴x2+10x=-23, 7分∴x2+10x+25=-23+25,即(x+5)2=2, 8分
∴x+5=± , 9分
∴x1=-5+ ,x2=-5- . 10分
20.[答案含评分细则](新考向·尺规作图)(6分)用圆规、无刻 度的直尺作图,不写作法,但要保留作图痕迹.已知:矩形ABCD.求作:菱形AECF,使点E,F分别在边BC,AD上. 
解析　如图,菱形AECF即为所作.  6分
21.[答案含评分细则](跨学科·物理)(2023吉林长春外国语实 验学校期末)(8分)如图,电路上有①②③3个开关和一个小灯 泡,若任意闭合电路上2个开关,用画树状图或列表的方法,求 小灯泡发光的概率. 
解析　①②③3个开关任意闭合其中2个开关,所有等可能出 现的结果如下:
 4分共有6种等可能的结果,其中小灯泡能发光的结果有4种,所以 ①②③3个开关任意闭合其中2个开关,小灯泡发光的概率为  = . 8分
22.[答案含评分细则](2023安徽萧县一模)(10分)为检测某品 牌一次性注射器的质量,将注射器里充满一定量的气体,当温 度不变时,注射器里的气体的压强p(kPa)与气体体积V(mL)满 足反比例函数关系,其图象如图所示.(1)求反比例函数的表达式.(2)当气体体积为60 mL时,求气体的压强.(3)如果注射器内气体的压强不能超过500 kPa,那么其体积V 要控制在什么范围?
解析    (1)设p= (k≠0),由题意知200= ,∴k=6 000,∴p= . 3分(2)当V=60 mL时,p= =100(kPa),∴气体的压强是100 kPa. 6分(3)当p=500 kPa时,V= =12(mL),∴气体的体积应不少于12 mL. 10分
23.[答案含评分细则](10分)一块材料(△ABC)的形状是等腰 三角形,底边BC=120 cm,高AD=120 cm.(1)若把这块材料加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB,AC上(如图1),则这个正方形的边 长为多少?(2)若把这块材料加工成正方体零件(如图2,阴影部分为正方 体展开图,M,N在AB,AC上,MN∥BC),则这个正方体的表面积 为多少?
解析    (1)设正方形的边长为x cm,∵AD是△ABC的高,∴∠ADB=90°. 1分∵四边形EFGH是正方形,∴EH∥BC, 2分∴∠AKE=∠ADB=90°,△AEH∽△ABC,∴ = , 4分∴ = ,∴x=60.答:这个正方形的边长为60 cm. 5分
(2)设小正方形的边长为a cm,即MN=a cm,∵AD为△ABC的高,∴∠ADB=90°. 6分∵MN∥BC,∴∠APM=∠ADB=90°,△AMN∽△ABC, 7分∴ = , 8分∴ = ,∴a=24,∴6a2=6×242=3 456.答:正方体的表面积为3 456 cm2. 10分
24.[答案含评分细则](2024四川巴中期末)(10分)某商店秋季 开学前,购进一批学生用双肩包进行销售,进货价和销售价如 下表(利润=销售价-进货价):
(1)商店用4 350元购进Ⅰ、Ⅱ类两款双肩包共100件,求两款 双肩包分别购进的件数.(2)开学季过后,商店老板打算把Ⅱ类学生用双肩包降价销 售,如果按照原价销售,平均每天可售6件.经调查发现,每件每 降价1元,平均每天可多售2件,将销售价定为每件多少元时, 才能使Ⅱ类学生用双肩包平均每天销售利润为72元?
解析    (1)设购进x件Ⅰ类学生用双肩包,y件Ⅱ类学生用双肩 包, 1分根据题意得  2分解得  4分答:购进35件Ⅰ类学生用双肩包,65件Ⅱ类学生用双肩包. 5分(2)设销售价定为每件m元,则每件的销售利润为(m-40)元,平 均每天可售出6+2(50-m)=(106-2m)件, 6分
根据题意得(m-40)(106-2m)=72, 7分整理得m2-93m+2 156=0, 8分解得m1=44,m2=49. 9分答:将销售价定为每件44元或49元时,才能使Ⅱ类学生用双肩 包平均每天销售利润为72元. 10分
25.[答案含评分细则](2023四川成都锦江一诊)(12分)如图1, ▱ABCD的各内角的平分线分别相交于点E,F,G,H.(1)求证:四边形EFGH为矩形.(2)如图2,当▱ABCD为矩形时.①求证:四边形EFGH为正方形.②若AD=10,四边形EFGH的面积为8,求AB的长.      
解析    (1)证明:∵AF平分∠BAD,BH平分∠ABC,∴∠EAB= ∠BAD,∠EBA= ∠ABC,在▱ABCD中,∵AD∥BC,∴∠DAB+∠ABC=180°,∴∠EAB+∠EBA= (∠DAB+∠ABC)=90°, 2分∴∠AEB=90°,∴∠HEF=90°,同理可得∠BHC=90°=∠AFD,∴四边形EFGH是矩形. 3分(2)①证明:∵四边形ABCD为矩形,∴AB=CD,AD=BC,∠ABC=∠BCD=∠CDA=∠BAD=90°, 4分
∵矩形ABCD的各内角的平分线分别相交于点E,F,G,H,∴∠EAB=∠FAD= ∠BAD=45°,∠EBA=∠HBC= ∠ABC=45°,∠BCH=∠GCD= ∠BCD=45°,∠ADF=∠GDC= ∠ADC=45°,∴∠EBA=∠EAB,∠BCH=∠HBC,∠GCD=∠GDC,∠FAD=∠ADF,△ABE≌△CDG(ASA),△ADF≌△CBH(ASA),∴AE=BE=DG=CG,AF=DF=HB=HC,∴EF=FG=GH=HE,∴四边形EFGH是菱形,