数学八年级上册第十六章 轴对称和中心对称16.2 线段的垂直平分图文课件ppt

这是一份数学八年级上册第十六章 轴对称和中心对称16.2 线段的垂直平分图文课件ppt，共20页。PPT课件主要包含了复习提问，引出问题，无数个，知识点，判定线段中垂线的方法，做一做等内容，欢迎下载使用。
1. 理解并掌握线段垂直平分线的逆定理并学会运用.2. 能够运用线段垂直平分线的性质定理和逆定理解决实际问题.3. 通过线段的垂直平分线性质定理的逆定理的证明过程,体验逻辑推理的数学方法.
给你已知线段AB，以AB为底边做等腰△PAB可以作几个？试着画一画！
在这里，我们利用了线段的垂直平分线上的点与这条线段两个端点的距离相等进行证明.
那么反过来，到线段两端距离相等的点在这条线段的垂直平分线上呢？
线段垂直平分线的性质的逆定理
1.写出线段垂直平分线的性质定理的逆命题.
2.结合下图，写出逆命题的已知和求证.
3.猜想这个逆命题的真假，并试着说明理由.
4.试着证明你的猜想.
到线段两端距离相等的点，在这条线段的垂直平分线上.
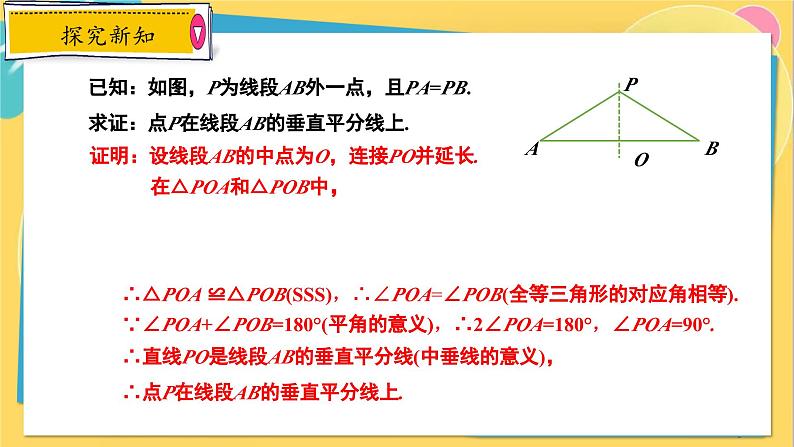
已知：P为线段AB外一点，且PA=PB.求证：点P在线段AB的垂直平分线上.
已知：如图，P为线段AB外一点，且PA=PB.求证：点P在线段AB的垂直平分线上.
证明：设线段AB的中点为O，连接PO并延长.
在△POA和△POB中，
∴△POA ≌△POB(SSS)，∴∠POA=∠POB(全等三角形的对应角相等).
∵∠POA+∠POB=180°(平角的意义)，∴2∠POA=180°，∠POA=90°.
∴直线PO是线段AB的垂直平分线(中垂线的意义)，∴点P在线段AB的垂直平分线上.
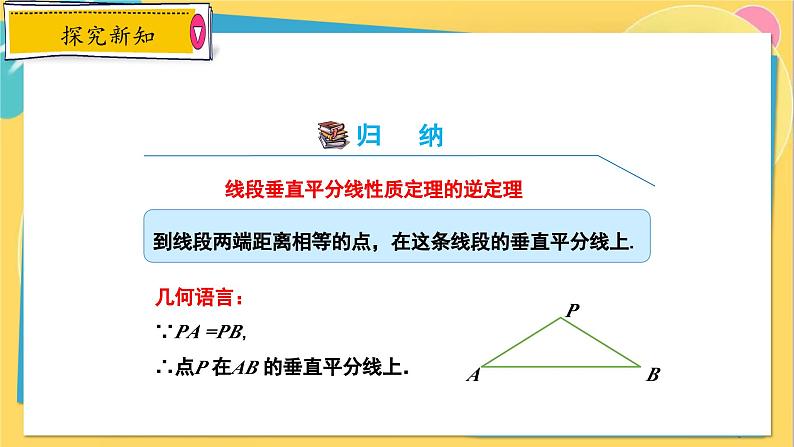
线段垂直平分线性质定理的逆定理
几何语言：∵PA =PB，∴点P 在AB 的垂直平分线上．
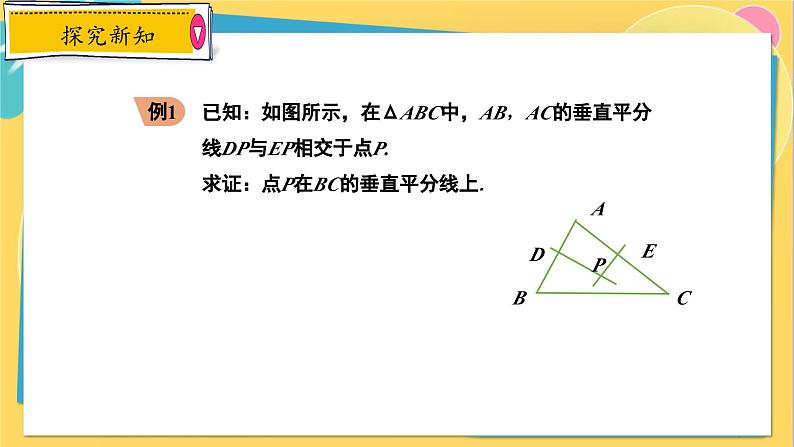
已知：如图所示，在ΔABC中，AB，AC的垂直平分线DP与EP相交于点P. 求证：点P在BC的垂直平分线上.
证明：如图所示，连接PA，PB，PC.
∵DP，EP分别是AB，AC的垂直平分线(已知)，∴PA=PB=PC(线段垂直平分线的性质定理).∴点P在BC的垂直平分线上(线段垂直平分线性质定理的逆定理).
三角形三边的中垂线相交于一点，这点到三角形三个顶点的距离相等.
1.锐角三角形ABC内有一点P，满足PA＝PB＝PC，则点P是△ABC(　　)A．三条角平分线的交点　　 　　　　　B．三条中线的交点C．三条高的交点　　 　　　　　D．三边垂直平分线的交点
2.如图所示，点D在△ABC的边BC上，且BC=BD+AD，则点D在(　　)的垂直平分线上. A. AB B. AC C. BC D. 不能确定
导引：∵BC=BD+AD=BD+CD，∴AD=CD，∴点D在AC的垂直平分线上.故选B.
1.若PA=PB，过点P作直线l，则l是线段AB的中垂线吗？
不一定是.因为经过一点的直线有无数条.
2.若PA=PB，同时MA=MB，则直线PM是线段AB的中垂线吗？
是，因为两点确定一条直线.
用线段中垂线性质定理的逆定理判定线段垂直平分线的步骤：
∵AB =AC，MB =MC，∴点A、M均在线段BC的中垂线上，　∵两点确定一条直线，∴AM垂直平分BC.
1. 用线段中垂线的定义.
2. 用线段中垂线性质定理的逆定理，推出两个点都在线段的中垂线上，则过这两个点的直线就是这条线段的中垂线.
已知：如图所示，在四边形ABCD中，AB=BC=CD=AD，AC⊥BD，垂足为O. 求证：AO=OC，BO=OD.
证明：因为AB=BC，CD=AD，所以点B，D均在线段AC的垂直平分线上，直线BD是线段AC的垂直平分线，所以AO=OC，同理，BO=DO.
1.如图，AC＝AD，BC＝BD，则有(　　) A．AB垂直平分CD B．CD垂直平分AB C．AB与CD互相垂直平分 D．以上都不正确
2. 如图，AD为△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF，交AD于点O，求证：AD垂直平分EF.
证明：∵AD为△ABC的角平分线，∴∠EAD=∠FAD，又∵DE⊥AB，DF⊥AC，∴∠AED=∠AFD=90°，又AD=AD，∴△AED≌△AFD（AAS)，∴AE=AF，DE=DF，∴AD垂直平分EF.
两个不同点的方位角问题
1. 如图， AC ＝ AD ， BC ＝ BD ，则有(　A　)
由垂直平分线的判定，可推出 AB 垂直平分 CD ，故 选A.
2. [母题·教材P116例2]如图，点 D 在△ ABC 的边 BC 上，且 BC ＝ BD ＋ AD ，则点 D 在某一线段的垂直平分线上.这 条线段是(　B　)
∵ BC ＝ BD ＋ DC ， BC ＝ BD ＋ AD ，∴ DC ＝ AD . ∴点 D 在线段 AC 的垂直平分线上.