初中冀教版16.2 线段的垂直平分教课内容ppt课件

这是一份初中冀教版16.2 线段的垂直平分教课内容ppt课件，共21页。PPT课件主要包含了学习目标，冀教版八上，不确定，可以作无数个，在一条直线上，作∠APB的角平分线，不一定是，判定线段中垂线的方法，线段中垂线的性质，你发现了什么结论等内容，欢迎下载使用。

1.理解并掌握线段垂直平分线的逆定理并学会运用.2.根据能够运用尺规作线段的垂直平分线.3.能够运用线段垂直平分线的性质定理和逆定理解决实际问题．
试一试:在练习本上以线段AB为底边做等腰△PAB.
△PAB的形状和大小是确定的吗？
符合条件的△PAB能作几个？
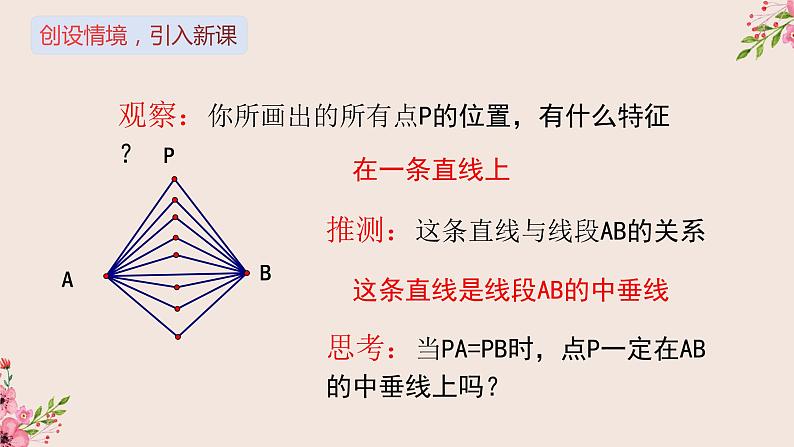
观察：你所画出的所有点P的位置，有什么特征？
推测：这条直线与线段AB的关系
这条直线是线段AB的中垂线
思考：当PA=PB时，点P一定在AB的中垂线上吗？
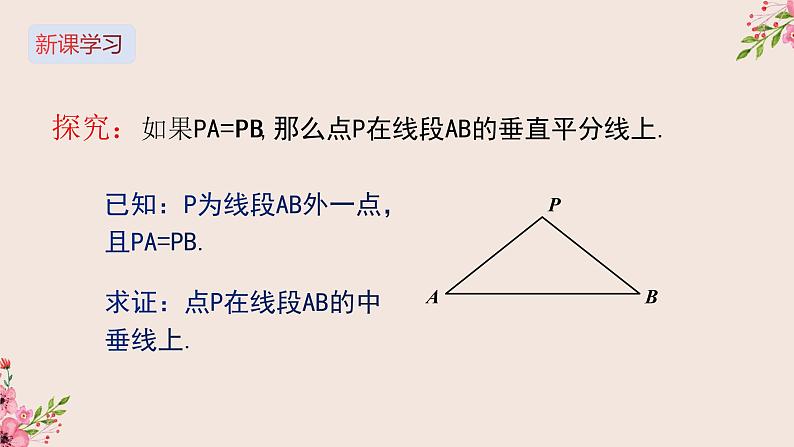
探究：如果PA=PB,那么点P在线段AB的垂直平分线上.
已知：P为线段AB外一点，且PA=PB.
求证：点P在线段AB的中垂线上.
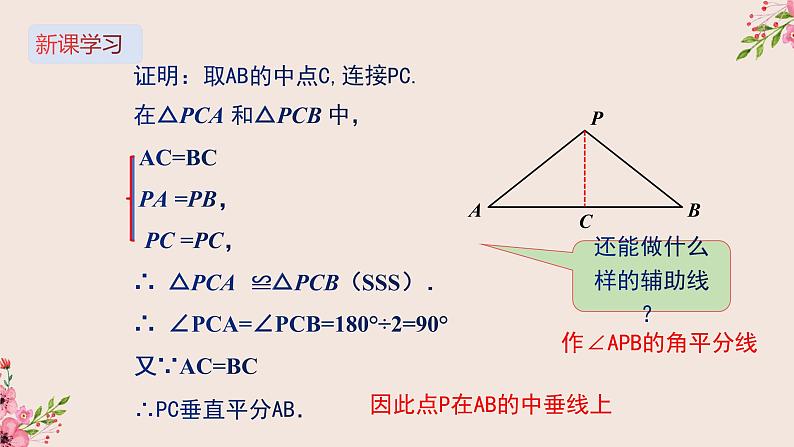
证明：取AB的中点C,连接PC.在△PCA 和△PCB 中， AC=BC PA =PB， PC =PC，∴ △PCA ≌△PCB（SSS）．∴ ∠PCA=∠PCB=180°÷2=90°又∵AC=BC∴PC垂直平分AB．
因此点P在AB的中垂线上
还能做什么样的辅助线？
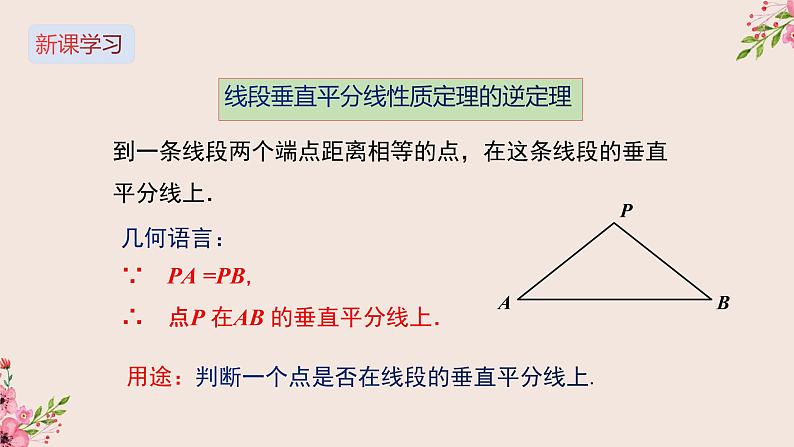
线段垂直平分线性质定理的逆定理
到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．
几何语言：∵　PA =PB，∴　点P 在AB 的垂直平分线上．
用途：判断一个点是否在线段的垂直平分线上.
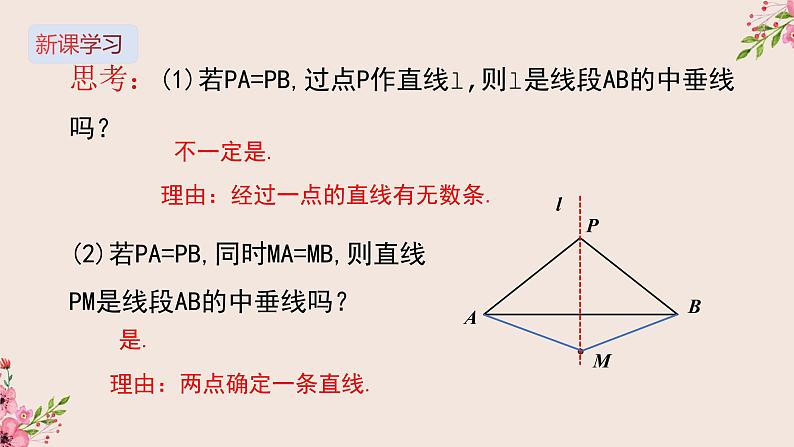
(2)若PA=PB,同时MA=MB,则直线PM是线段AB的中垂线吗？
理由：经过一点的直线有无数条.
思考：(1)若PA=PB,过点P作直线l,则l是线段AB的中垂线吗？
理由：两点确定一条直线.
∵　AB =AC，MB =MC，∴点A、M均在线段BC的中垂线上　两点确定一条直线∴AM垂直平分BC
用线段中垂线性质定理的逆定理判定线段垂直平分线的步骤：
1.用线段中垂线的定义.
2.用线段中垂线性质定理的逆定理，推出两个点都在线段的中垂线上，则过这两个点的直线就是这条线段的中垂线.
1.已知，MN是线段AB的中垂线，下列说法正确的是（ ）
A.与AB距离相等的点在MN上 B.与点A和点B距离相等的点在MN上C.与MN距离相等的点在AB上D.AB垂直平分MN
2.如图，点D在△ABC的边BC上，且BC=BD+DA,则点D在线段_____的垂直平分线上.
例1.已知：如图16-13，△ABC的边AB、AC的垂直平分线相交于点P 求证：点P在BC的垂直平分线上
（1）已知条件提示用什么知识点？
（2）怎样才能得到结论？
线段中垂线的性质的逆定理
证明：连接PA、PB、PC ∵ 点P在AB、AC的垂直平分线上（已知） ∴ PA＝PB，PA＝PC（线段垂直平分线上的点与线段两端距离相等） ∴ PB＝PC（等式性质） ∴ 点P在BC的垂直平分线上（与线段两端距离相等的点在这条线段的垂直平分线上)
三角形的三边的中垂线相交于一点，这点到三角形三个顶点的距离相等.
1.已知：点C,D为线段AB外两点，下列说法正确的是（ ）.
A.若AC=BC，则经过点C的直线垂直AB B.若AC=BC,AD=BD则直线CD垂直ABC.若AD=BD,则经过点D的直线垂直ABD.若CD⊥AB,则AC=BC,AD=BD
2.如图，A,B,C表示三个居民小区，为丰富居民的文化生活，现准备建一个文化广场，使它到三个小区的距离相等，则文化广场应建在（ ）.
A.AC,BC两边高线的交点处 B.AC,BC两边中线的交点处C.AC,BC两边中垂线的交点处D.∠A,∠B两内角平分线的交点处
3.如图，AD为△ABC的角平分线，DE⊥AB于点E,DF⊥AC于点F,连接EF角AD于点O,求证：AD垂直平分EF.
由△AED≌△AFD可得
AE=AF,DE=DF
4.如图，四边形ABCD是一个“风筝”骨架，其中AB=AD,CB=CD.
(1)小明认为四边形ABCD的两条对角线AC⊥BD,垂足为E,并且BE=EB,你同意他的说法吗？
同意，由AB=AD,CB=CD可得到AC是BD的垂直平分线.
(2)设对角线AC=a,BD=b,请用含a,b的式子表示四边形ABCD的面积.
线段的垂直平分的性质定理的逆定理
到线段的两个端点距离相等的点在线段的垂直平分线上
判断一个点是否在线段的垂直平分线上