





浙教版九年级上册1.4 二次函数的应用课前预习ppt课件
展开会运用一元二次方程求函数的图象与x轴或平行于x轴的直线的交点坐标,并用来解决相关的实际问题.会用二次函数的图象求一元二次方程的解或近似解.理解问题解决过程中二次函数与一元二次方程两种数学模型的转换,明确它们之间的区别与联系.
1.前面我们思考并讨论过二次函数y=ax2+bx+c和一元二次方程ax2+bx+c=0的关系,你还记得吗?
(一元二次方程的一般式)
令函数值y=0的自变量x的值
方程ax2+bx+c=0的解
函数图象与x轴交点的横坐标
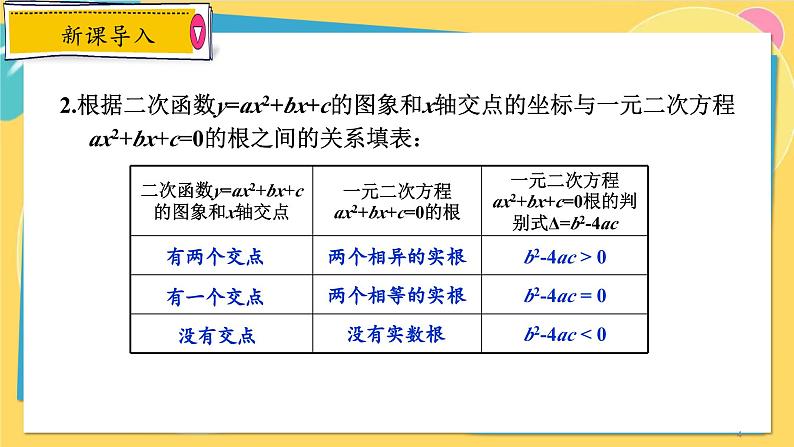
2.根据二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根之间的关系填表:
二次函数与一元二次方程的关系
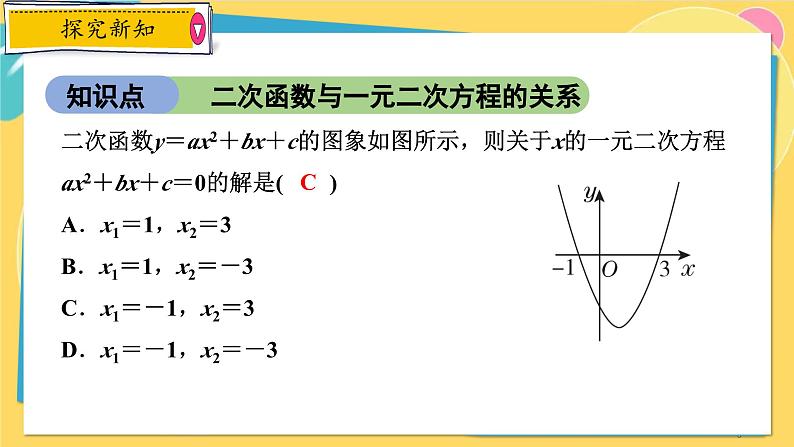
二次函数y=ax2+bx+c的图象如图所示,则关于x的一元二次方程ax2+bx+c=0的解是( )A.x1=1,x2=3 B.x1=1,x2=-3C.x1=-1,x2=3 D.x1=-1,x2=-3
【分析】抛物线与x轴的交点坐标为(-1,0),(3,0),则关于x的一元二次方程ax2+bx+c=0的解为x1=-1,x2=3.
利用一元二次方程ax2+bx+c=m求二次函数图象与x轴或平行于x轴的直线的交点坐标,并解相关实际问题(如“抛物线型”)的一般思路:
(1)根据题意建立直角坐标系,并求出抛物线型对应的二次函数(y=ax2+bx+c) 表达式;(2)取y=m,得一元二次方程ax2+bx+c=m ;(3)解这个方程;(4)根据实际情况写出题目答案.
二次函数y=ax²+bx+c
一元二次方程ax²+bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:(m,0);(n,0)
反过来,也可利用二次函数的图象求一元二次方程的解。
可以利用解一元二次方程求二次函数的图象与横轴(或平行于横轴的直线)的交点坐标.反之,也可以利用二次函数的图象求一元二次方程的解.
【点拨】根据已知条件,易求出函数表达式h = 10t-5t²和画出函数图象.
取h=3.75m,得方程10t-5t²=3.75,求出它的根,就得到球达到3.75m高度时所经过的时间.
解:由题意,得h(m)关于t(s)的二次函数表达式为h=10t-5t². 取h=0,得一元二次方程10t-5t²=0,解这个方程得,t1=0,t2=2.所以球从地面弹起至回地面所需的时间为t2-t1=2(s).
取h=3.75,得一元二次方程10t-5t²=3.75.解这个方程,得t1=0.5,t2=1.5.答:球从地面弹起至回地面所需的时间为2s,经过0.5s或1.5s球的高度达到3.75m.
一元二次方程的解或近似解
(1) 将原方程变形为x2+2x-10=0;(2) 用描点法作二次函数y=x2+2x-10的图象;
利用二次函数的图象求一元二次方程x2+2x=10的近似根,并说出你的做法步骤.
(3) 观察图象,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.3和2.3.
(4) 写出方程x2+2x-10=0的解:由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
方程x2+2x=7的近似根呢?
方程x2+2x=7即x2+2x-10=-3,
当y=x2+2x-10的函数值为-3时,如图所示.
由此可知,方程x2+2x-10=0的近似根为:x1≈-3.9,x2≈1.9(可借助计算器验证及确定其近似值).
二次函数 y=ax2+bx+c的图象与 x 轴的公共点的横坐标是一元二次方程 ax2+bx+c =0 的解,因此可以借助二次函数的图象求一元二次方程的解 .
利用二次函数图象求一元二次方程的近似根的步骤:(1)画出函数的图象,并由图象确定方程根的个数;(2)由图象交点位置确定横坐标的范围;(3)估计方程的近似根.
利用二次函数的图象求一元二次方程 x²+x-1= 0 的近似解。
【点拨】设y=x2+x-1,则方程的解就是该函数图象与x轴交点的横坐标.可以画出函数图象,通过观察图象得到近似解.
解:设y= x²+x-1,则方程x²+x-1=0的解就是该函数图象与x轴交点的横坐标.画出函数y= x²+x-1的图象,得到图象与x轴的交点A,B.点A的横坐标x1≈0.6,点B的横坐标x2≈-1.6.
所以方程的近似解为x1≈0.6, x2≈-1.6.
【归纳】用求根公式求出方程x²+x - 1=0的近似解,并由检验例2中所给图象解法的精确度。
如果把方程x²+x - 1 = 0变形成 x² = - x+1,那么方程的解也可以看成怎样的两个函数的交点的横坐标?
用不同图象解法试一试,结果相同吗?
在不使用计算机画图象的情况下,你认为哪一种方法较为方便?
二次函数与不等式的关系
若二次函数y=ax2+bx+c(a≠0,且a,b,c为常数)的图象如图所示,则关于x的不等式a(x+2)2+b(x+2)+c<0的解集为__________________.
二次函数y=ax2+bx+c的图象如图所示,则关于x的 一元二次方程ax2+bx+c=0的解是( )A.x1=1,x2=3 B.x1=1,x2=-3C.x1=-1,x2=3 D.x1=-1,x2=-3
【2024·台州路桥区期末】二次函数y=ax2+bx+c的部分图象如图所示,图象经过点(1,0),且对称轴为直线x=-1,则一元二次方程ax2+bx+c=0的根是________________.
【2023·台州椒江区期末】二次函数y=ax2+bx+c的自变量x与函数值y的对应关系如下表,设一元二次方程ax2+bx+c=0的根为x1,x2,且x1<x2,则下列说法正确的是( ) A.-1.5
初中数学人教版九年级上册21.1 一元二次方程多媒体教学ppt课件: 这是一份初中数学人教版九年级上册21.1 一元二次方程多媒体教学ppt课件,共27页。PPT课件主要包含了学习目标,有两个不相等的实数根,有两个相等的实数根,没有实数根,b2-4ac,活动1,活动2,自由讨论,问题2,答2个1个0个等内容,欢迎下载使用。
人教版九年级上册21.1 一元二次方程多媒体教学ppt课件: 这是一份人教版九年级上册21.1 一元二次方程多媒体教学ppt课件,共20页。PPT课件主要包含了有两个不相等的实数根,有两个相等的实数根,没有实数根,b2-4ac,活动1,活动2,自由讨论等内容,欢迎下载使用。
数学九年级上册21.1 一元二次方程课堂教学课件ppt: 这是一份数学九年级上册21.1 一元二次方程课堂教学课件ppt,共25页。PPT课件主要包含了b2-4ac,活动1,活动2,自由讨论,问题2,答2个1个0个,x1-2x21,x1x23,1有两个交点,2有一个交点等内容,欢迎下载使用。













