初中数学人教版九年级下册26.2 实际问题与反比例函数精品ppt课件

这是一份初中数学人教版九年级下册26.2 实际问题与反比例函数精品ppt课件，共30页。PPT课件主要包含了学习目标，有两个不相等的实数根，有两个相等的实数根，没有实数根，活动1，活动2，自由讨论，问题2，边观察边思考，走近中考等内容，欢迎下载使用。

1、学习二次函数与一元二次方程的关系
2、会用一元二次方程解决二次函数图象 与x轴的交点问题
在现实生活中，我们常常会遇到与二次函数及其图象有关的问题。　　如：被抛射出去的物体沿抛物线轨道飞行；抛物线形拱桥的跨度、拱高的计算等．　　利用二次函数的有关知识研究和解决这些问题，具有很现实的意义。　　本节课，我将和同学们共同研究解决这些问题的方法，探寻其中的奥秘。
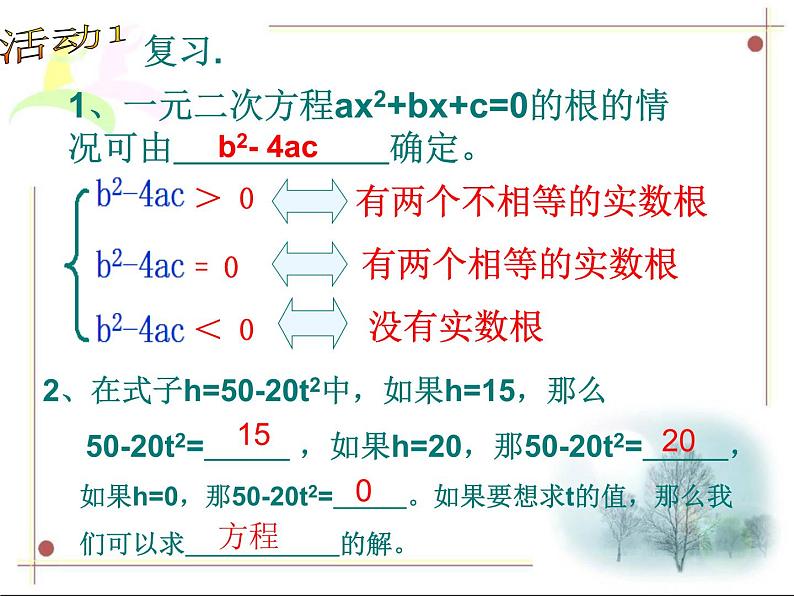
1、一元二次方程ax2+bx+c=0的根的情况可由 确定。
2、在式子h=50-20t2中，如果h=15，那么 50-20t2= ，如果h=20，那50-20t2= ， 如果h=0，那50-20t2= 。如果要想求t的值，那么我 们可以求 的解。
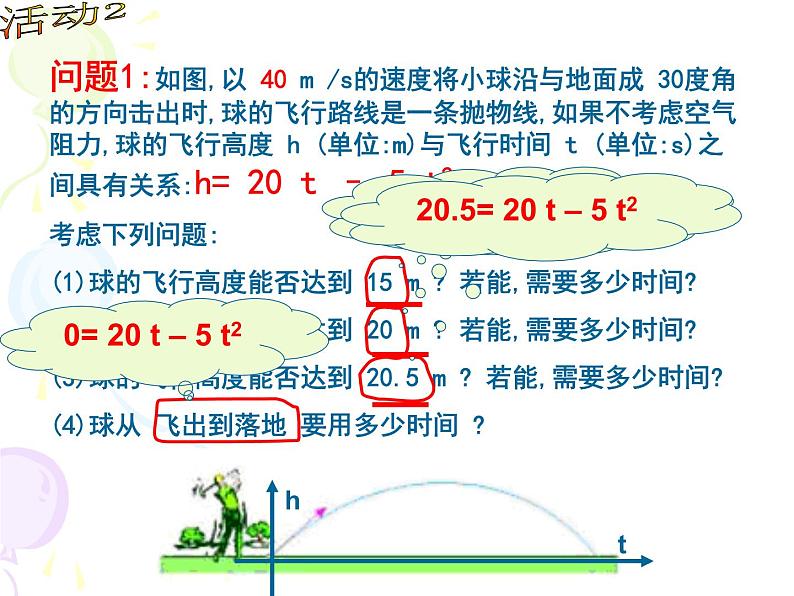
问题1:如图,以 40 m /s的速度将小球沿与地面成 30度角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20 t – 5 t2 考虑下列问题:(1)球的飞行高度能否达到 15 m ? 若能,需要多少时间?(2)球的飞行高度能否达到 20 m ? 若能,需要多少时间?(3)球的飞行高度能否达到 20.5 m ? 若能,需要多少时间?(4)球从 飞出到落地 要用多少时间 ?
0= 20 t – 5 t2
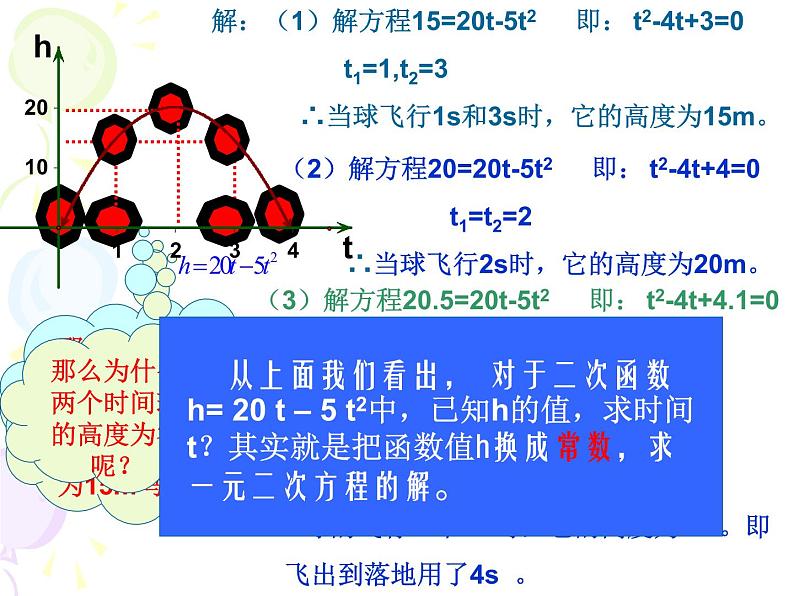
解：（1）解方程15=20t-5t2 即： t2-4t+3=0 t1=1,t2=3 ∴当球飞行1s和3s时，它的高度为15m。
（2）解方程20=20t-5t2 即： t2-4t+4=0 t1=t2=2 ∴当球飞行2s时，它的高度为20m。
（3）解方程20.5=20t-5t2 即： t2-4t+4.1=0 因为(-4)2-4×4.1＜0，所以方程无解， ∴球的飞行高度达不到20.5m。
（4）解方程0=20t-5t2 即： t2-4t=0 t1=0,t2=4 ∴球的飞行0s和4s时，它的高度为0m。即 飞出到落地用了4s 。
你能结合图形指出为什么在两个时间球的高度为15m吗？
那么为什么只在一个时间求得高度为20m呢？
那么为什么两个时间球的高度为零呢？
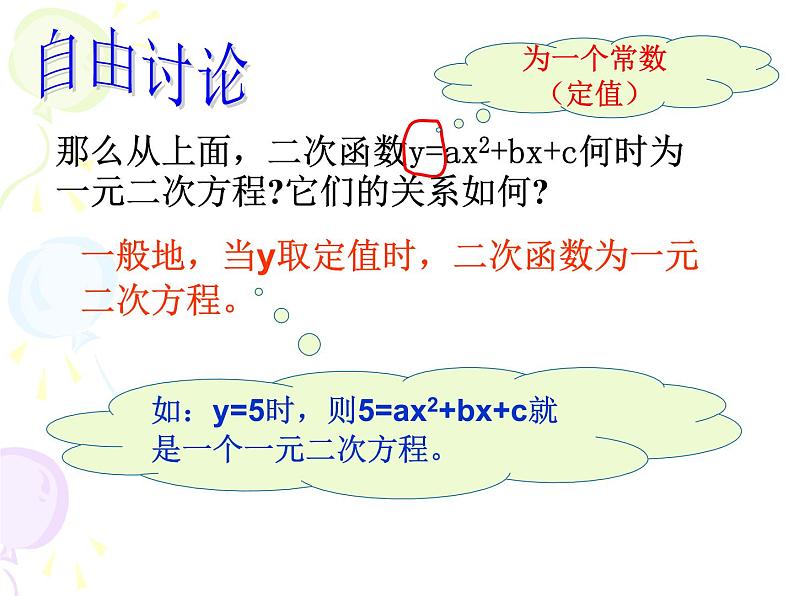
那么从上面，二次函数y=ax2+bx+c何时为一元二次方程?它们的关系如何?
一般地，当y取定值时，二次函数为一元二次方程。
如：y=5时，则5=ax2+bx+c就是一个一元二次方程。
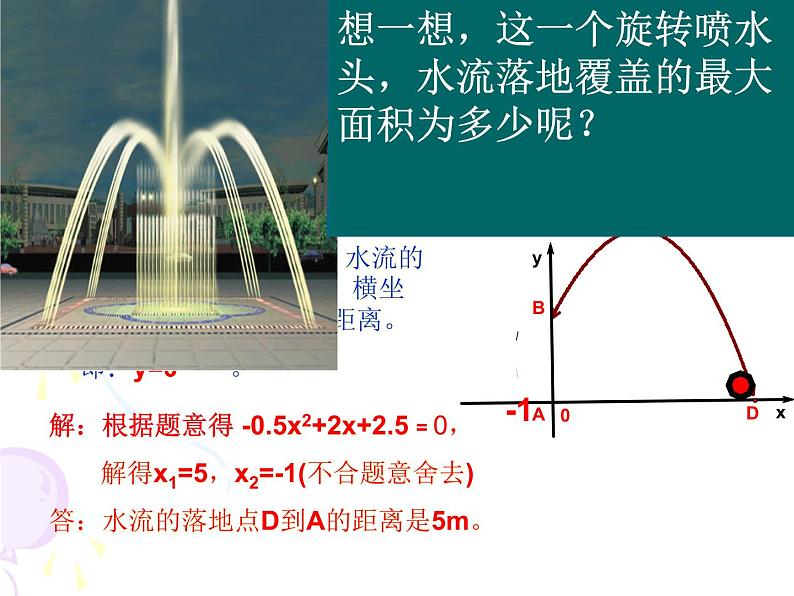
练习一：如图设水管AB的高出地面2.5m，在B处有一自动旋转的喷水头，喷出的水呈抛物线状，可用二次函数y=-0.5x2+2x+2.5描述，在所有的直角坐标系中，求水流的落地点D到A的距离是多少？
解：根据题意得 -0.5x2+2x+2.5 = 0， 解得x1=5，x2=-1(不合题意舍去)答：水流的落地点D到A的距离是5m。
分析：根据图象可知，水流的落地点D的纵坐标为0，横坐标即为落地点D到A的距离。即：y=0 。
1、二次函数y = x2+x-2 , y = x2 - 6x +9 , y = x2 – x+ 1的图象如图所示。
(1).每个图象与x轴有几个交点？(2).一元二次方程? x2+x-2=0 , x2 - 6x +9=0有几个根? 验证一下一元二次方程x2 – x+ 1 =0有根吗?(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与 一元二次方程ax2+bx+c=0的根有什么关系?
b2 – 4ac ＞0
b2 – 4ac =0
b2 – 4ac ＜0
2、二次函数y=ax2+bx+c的图象和x轴交点,则b2-4ac的情况如何。
二次函数与一元二次方程
2、二次函数y=ax2+bx+c的图象和x轴交点 情况如何？（b2-4ac如何） (1)有两个交点 (2)有一个交点 (3)没有交点
b2 – 4ac > 0
b2 – 4ac= 0
b2 – 4ac< 0
思考：若抛物线y=ax2+bx+c与x轴有交点,则 b2-4ac .
练习:看谁算的又快又准。
1.不与x轴相交的抛物线是( ) A y=2x2 – 3 B y= - 2 x2 + 3 C y= - x2 – 2x D y=-2(x+1)2 - 3
2.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=＿＿,此时抛物线 y=x2-2x+m与x轴有＿ 个交点.
3.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=＿＿＿＿.
4.抛物线y=x2-3x+2 与y轴交于点＿＿＿＿,与x轴交于点＿＿＿ ＿.
5.如图,抛物线y=ax2+bx+c的对称轴是直线 x=-1,由图象知,关于x的方程ax2+bx+c=0的两个根分别是x1=1.3 ,x2=＿＿＿
6.已知抛物线y=kx2-7x-7的图象和x轴有交点，则 k的取值范围（ ）
6.某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料长(图中所有黑线的长度和)为10米.当x等于多少米时,窗户的透光面积最大? 最大面积是多少?
●请你把这节课你学到了东西告诉你的同 桌，然后告诉老师？
二次函数与x轴的交点的横坐标是一元二次方程的解
1、二次函数y=x2+x-6的图象与x轴交点横坐标是（ ）
A：2和-3 B：-2和3 C：2和3 D：-2和3
2、已知实数s、t，且满足s2+s-2006=0，t2+t-2006=0，那么二次函数y=x2+x-2006的图象大致是（ ）
3、已知抛物线y=x2+mx-2m2(m≠0) 求证：该抛物线与x轴有两个不同的交点。
证明：∵b2-4ac=m2-4×1×（-2m2) =9m2
∵ m≠0 ∴9m2>0 即b2-4ac>0
∴抛物线与x轴有两个不同的交点
你会利用二次函数的图象求一元二次方程2x2-4x+1=0的近似根吗？
1.二次函数 的图象如图4所示，则下列说法不正确的是（ ）
2.二次函数y = ax2 + bx + c的部分对应值如下表：
利用二次函数的图象可知，当函数值y＜0时，x的取值范围是（ ）．
A．x＜0或x＞2 B．0＜x＜2　　C．x＜－1或x＞3 D．－1＜x＜3
3.二次函数的图象 与轴有交点，则的取值范围是【　】
4.下列命题：①若 ， 则 ； ②若 ，则一元二次方程 有两个不相等的实数根；③若 , 则一元二次方程 有两个不相等的实数根；④若 ，则二次函数的图像与坐标轴的公共点的个数是2或3.其中正确的是（　　）．Ａ.只有①②③ Ｂ．只有①③④ Ｃ．只有①④ Ｄ． 只有②③④．
5.王强在一次高尔夫球的练习中，在某处击球，其飞行路线满足抛物线 ，其中y（m）是球的飞行高度,x（m）是球飞出的水平距离，结果球离球洞的水平距离还有2m．（1）请写出抛物线的开口方向、顶点坐标、对称轴．（2）请求出球飞行的最大水平距离．（3）若王强再一次从此处击球，要想让球飞行的最大高度不变且球刚好进洞，则球飞行路线应满足怎样的抛物线，求出其解析式．
解：（1）抛物线 开口向下，顶点为 ，对称轴为（2）令 ，得：解得： ，∴球飞行的最大水平距离是8m．（3）要让球刚好进洞而飞行最大高度不变，则球飞行的最大水平距离为10m 抛物线的对称轴为 ，顶点为 设此时对应的抛物线解析式为 又 ∵点 在此抛物线上， ∴
课本：p23页 复习巩固 第1题 拓展探索 第6题
选做题：如图，一位篮球运动员跳起投篮，球沿抛物线 y＝－x2＋3.5运行，然后准确落人篮框内。已知篮框的 中心离地面的距离为3.05米。(1)球在空中运行的最大高度为多少米?(2)如果该运动员跳投时，球出手离地面的高度为2.25米，请问他距离篮框中心的水平距离是多少?
弄清一种关系------函数与一元二次方程的关系