






还剩15页未读,
继续阅读
数学21.2.2 公式法教学ppt课件
展开
这是一份数学21.2.2 公式法教学ppt课件,共23页。PPT课件主要包含了学习目标,探究新知,复习导入,①移项,②二次项系数化为1,③配方,④开平方求根,求根公式的推导,移项得,配方得等内容,欢迎下载使用。
1.理解一元二次方程的求根公式的推导过程,了解公式法的概念,会熟练应用公式法解一元二次方程2.会用一元二次方程根的判别式判断一元二次方程根的情况,并能根据根的情况,确定方程中字母系数的取值范围
用配方法解一元二次方程的步骤有哪几步?
前面我们学习过直接开平方法解一元二次方程,但它有一定的局限性,只对平方式等于非负数的特殊二次方程有效,因此我们又学习了配方法解一元二次方程.
任何一个一元二次方程都可以写成一般形式 ax2+bx+c=0 能否也用配方法得出它的解呢?
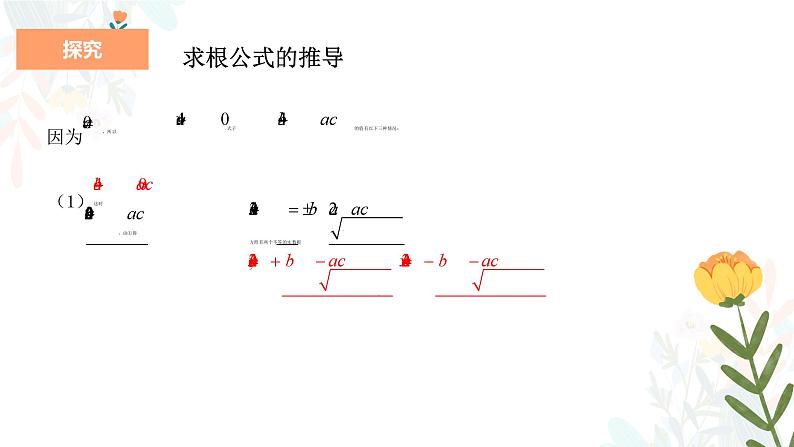
用配方法解一般形式的一元二次方程 ax2+bx+c=0 (a≠0).
方程两边都除以a,得
一元二次方程根的判别式
2.公式法:解一个具体的一元二次方程时,把各项系数直接代入求根公式,可以避免配方过程而直接得出跟,这种解一元二次方程的方法叫做公式法.
例2 用公式法解下列方程
1.变形: 化已知方程为一般形式; 2.确定系数:用a,b,c写出各项系数;3.计算: b2-4ac的值; 4.判断:若b2-4ac ≥0,则利用求根公式求出; 若b2-4ac<0,则方程没有实数根.
一化(一般形式);二定(系数值);三求( b2-4ac值);四判(方程根的情况);五代(求根公式计算).
务必将方程化为一般形式
1.理解一元二次方程的求根公式的推导过程,了解公式法的概念,会熟练应用公式法解一元二次方程2.会用一元二次方程根的判别式判断一元二次方程根的情况,并能根据根的情况,确定方程中字母系数的取值范围
用配方法解一元二次方程的步骤有哪几步?
前面我们学习过直接开平方法解一元二次方程,但它有一定的局限性,只对平方式等于非负数的特殊二次方程有效,因此我们又学习了配方法解一元二次方程.
任何一个一元二次方程都可以写成一般形式 ax2+bx+c=0 能否也用配方法得出它的解呢?
用配方法解一般形式的一元二次方程 ax2+bx+c=0 (a≠0).
方程两边都除以a,得
一元二次方程根的判别式
2.公式法:解一个具体的一元二次方程时,把各项系数直接代入求根公式,可以避免配方过程而直接得出跟,这种解一元二次方程的方法叫做公式法.
例2 用公式法解下列方程
1.变形: 化已知方程为一般形式; 2.确定系数:用a,b,c写出各项系数;3.计算: b2-4ac的值; 4.判断:若b2-4ac ≥0,则利用求根公式求出; 若b2-4ac<0,则方程没有实数根.
一化(一般形式);二定(系数值);三求( b2-4ac值);四判(方程根的情况);五代(求根公式计算).
务必将方程化为一般形式












