人教版九年级数学上册同步精品课堂 23.1.2 旋转作图（课件）

这是一份人教版九年级数学上册同步精品课堂 23.1.2 旋转作图（课件），共19页。

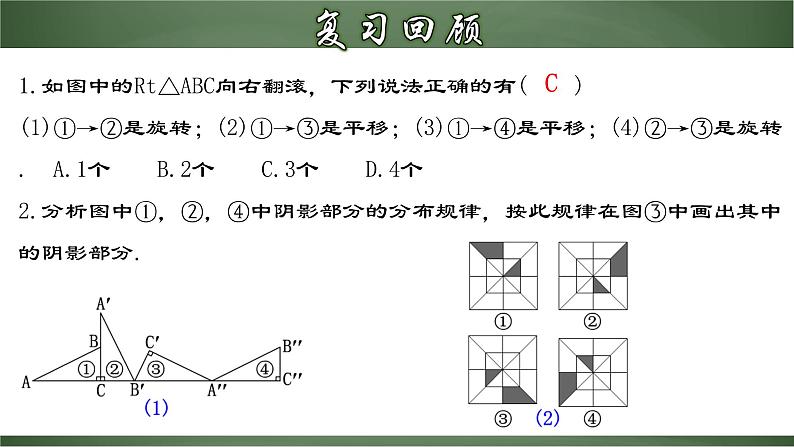
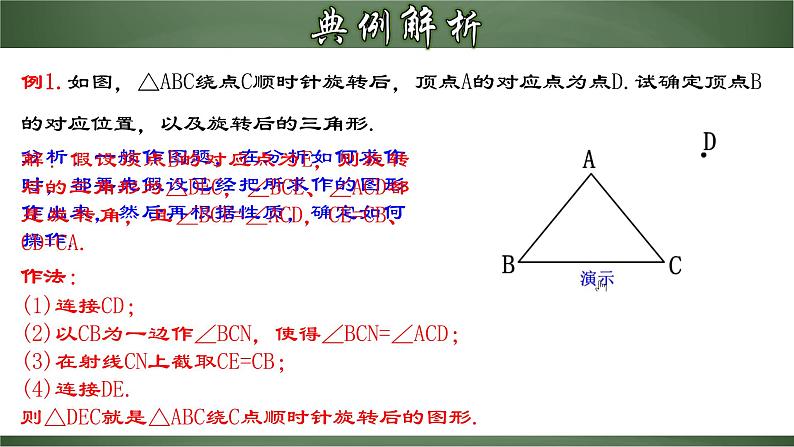
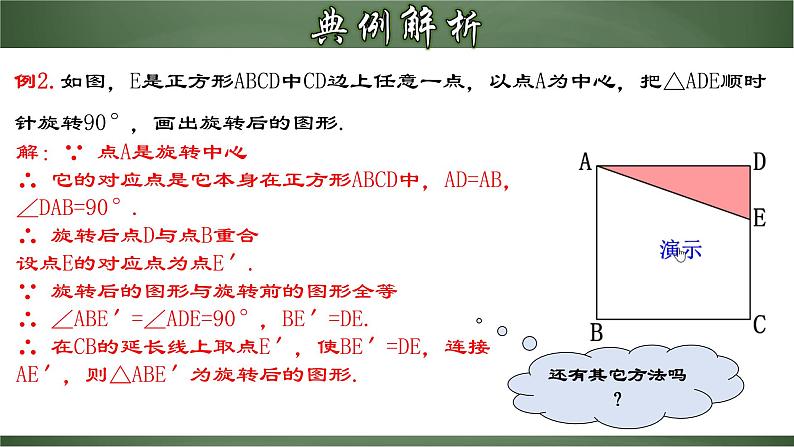
旋转作图1.运用旋转的基本性质将简单图形通过作图变化为复杂图形; (重点)2.能够根据旋转的基本性质解决实际问题和掌握旋转作图的步骤. (难点)1.旋转的概念2.旋转的性质 3.旋转的三要素 把一个平面图形绕着平面内某一点O转动一个角度，叫做图形的旋转，点O叫做旋转中心，转动的角叫做旋转角.旋转中心、旋转方向、旋转角.对应点到旋转中心的距离相等. 对应点与旋转中心所连线段的夹角等于旋转角. 旋转前、后的图形全等.1.如图中的Rt△ABC向右翻滚，下列说法正确的有( ) (1)①→②是旋转；(2)①→③是平移；(3)①→④是平移；(4)②→③是旋转. A.1个 B.2个 C.3个 D.4个2.分析图中①，②，④中阴影部分的分布规律，按此规律在图③中画出其中的阴影部分.C例1.如图，△ABC绕点C顺时针旋转后，顶点A的对应点为点D.试确定顶点B的对应位置，以及旋转后的三角形.分析：一般作图题，在分析如何求作时，都要先假设已经把所求作的图形作出来，然后再根据性质，确定如何操作.解：假设顶点B的对应点为E，则旋转后的三角形为△DEC，∠BCE、∠ACD都是旋转角，且∠BCE=∠ACD，CE=CB、CD=CA.作法：(1)连接CD；(2)以CB为一边作∠BCN，使得∠BCN=∠ACD；(3)在射线CN上截取CE=CB；(4)连接DE.则△DEC就是△ABC绕C点顺时针旋转后的图形.例2.如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.解：∵ 点A是旋转中心∴ 它的对应点是它本身在正方形ABCD中，AD=AB，∠DAB=90°.∴ 旋转后点D与点B重合设点E的对应点为点E′.∵ 旋转后的图形与旋转前的图形全等∴ ∠ABE′=∠ADE=90°，BE′=DE.∴ 在CB的延长线上取点E′，使BE′=DE，连接AE′，则△ABE′为旋转后的图形.还有其它方法吗？例2.如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.解：∵ 点A是旋转中心∴ 它的对应点是它本身在正方形ABCD中，AD=AB，∠DAB=90°.∴ 旋转后点D与点B重合设点E的对应点为点E′.∵ 对应点到旋转中心的距离相等，对应点与旋转中心所连线段的夹角等于旋转角.∴ AE′=AE，∠EAE′=∠DAB=90°.∴ 在AB左侧，作AE′⊥AE，使AE′=AE，连接BE′，则△ABE′为旋转后的图形1.旋转作图的条件： (1)有原图形 (2)有旋转中心 (3)有旋转方向 (4)有旋转角2.旋转作图的步骤： (1)确定图形的关键点； (2)作出旋转后的对应点； (3)顺次连线即可.①相同：都是一种运动；运动前后不改变图形的形状和大小.BACO②不同平移和旋转的异同： 将下列图案(点击图案可选择不同的图案)进行旋转，选择不同的旋转中心(点O可拉动)，不同的旋转角，会出现不同的效果.1.选择不同的__________、不同的________旋转同一个图案,会出现不同的效果.(1)两个旋转中，旋转中心不变, ______改变了，产生了_______的旋转效果.(2)两个旋转中,旋转角不变,__________改变了，产生了_______的旋转效果.旋转中心旋转角旋转角不同旋转中心不同旋转设计作图1.下列图案中，不能由一个基本图形通过旋转而构成的是( )2.如图，该图形在绕中心点按下列角度旋转后，不能与其自身重合的是( )A.72° B.108° C.144 D. 216° C B  C B5.等边三角形绕着它的中心旋转，若旋转后的三角形能与自身重合，则旋转角最小是______.6.如图，五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心至少经过_____次旋转而得到，每一次旋转______度.7.如图，是一个旋转对称图形，要使它旋转后与自身重合，至少应将它绕中心逆时针方向旋转_____度.120°472608.如图，E、F分别是正方形ABCD的边BC、CD.上的点，且BE=CF，连接AE, BF,将△ABE绕正方形的中心按逆时针方向转到△BCF，旋转角为a(0°