沪科版八年级下册18.1 勾股定理作业ppt课件

这是一份沪科版八年级下册18.1 勾股定理作业ppt课件，共22页。PPT课件主要包含了1求BF的长等内容，欢迎下载使用。

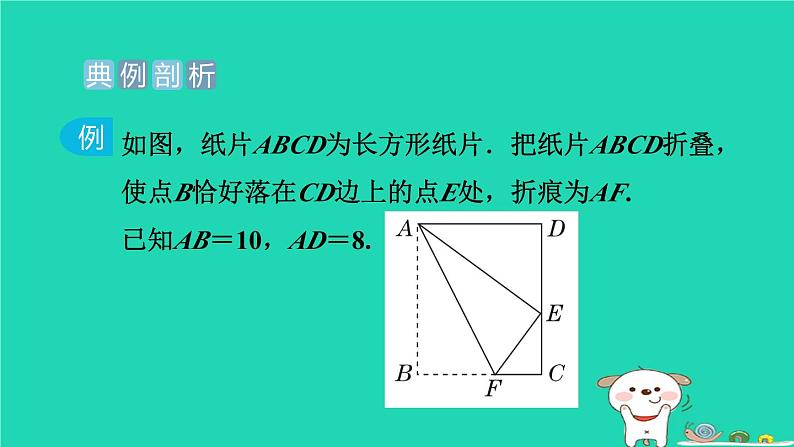
如图，纸片ABCD为长方形纸片．把纸片ABCD折叠，使点B恰好落在CD边上的点E处，折痕为AF.已知AB＝10，AD＝8.
解题秘方：翻折问题常常在三角形和四边形中出现，翻折前后的两个图形是全等图形，利用翻折求线段长时，一般都利用勾股定理建立方程模型解决问题．
(2)求折痕AF的长．
1. [2023·济南历城区期末]如图，在四边形ABCD中，∠A＝90°，AB＝8 cm，AD＝4 cm，BC＝CD，E是AB上一点，若沿CE折叠，则B，D两点重合，则DE的长为________．
2. [新考法·变式探究法]在△ABC中，∠C＝90°，AC＝6，BC＝8，D，E分别是斜边AB和直角边CB上的点，把△ABC沿着直线DE折叠，顶点B的对应点是B′.
(1)如图①，如果点B′和顶点A重合，求CE的长；
(2)如图②，如果点B落在AC边上，求CE的取值范围．
3. 【2022·丽水】如图，将长方形纸片ABCD折叠，使点B与点D重合，点A落在点P处，折痕为EF.
(1)求证：△PDE≌△CDF；
证明：∵四边形ABCD是长方形，∴∠A＝∠ADC＝∠B＝∠C＝90°，AB＝CD.由折叠得AB＝PD，∠A＝∠P＝90°，∠B＝∠PDF＝90°，∴PD＝CD，∠PDF＝∠ADC.
(2)若CD＝4 cm，EF＝5 cm，求BC的长．
4.如图，将长方形纸片ABCD沿EF折叠，使点C与点A重合，点D落在点D′处，折痕分别交AD，BC于点E，F，连接CE.
(1)求证：AE＝AF＝CE＝CF；
证明：由题意知AF＝CF，AE＝CE，∠AFE＝∠CFE.∵四边形ABCD是长方形，∴AD∥BC，∴∠AEF＝∠CFE.∴∠AFE＝∠AEF.∴AE＝AF.∴AE＝AF＝CE＝CF.
(2)设AE＝a，ED＝b，DC＝c，请写出一个a，b，c三者之间的数量关系式．
解：由题意知AE＝CE＝a.由∠D＝90°知ED2＋DC2＝CE2，即b2＋c2＝a2.
(1)求线段AB的长；
(2)若在y轴上有点P，使得S△PAB＝5，求点P的坐标；
(3)求点C的坐标和直线CD的函数表达式．
解：由题意知AB＝AC，∴OC＝OA＋AB＝3＋5＝8. ∴C(8，0)．设点D(0，m)，则OD＝－m，∴BD＝CD＝4－m.在Rt△OCD中，CD2＝OC2＋OD2，即(4－m)2＝82＋(－m)2，解得m＝－6，∴D(0，－6)．