初中数学7.1 探索直线平行的条件优质课件ppt

这是一份初中数学7.1 探索直线平行的条件优质课件ppt，共29页。PPT课件主要包含了教学目标，三线八角与同旁内角，不平行，同旁内角，三线八角，平行线的判定三，平行线的判定方法，知识精讲，a∥c等内容，欢迎下载使用。

借助于“三线八角”理解同旁内角的概念
区分同位角、内错角与同旁内角，并能根据“三线八角”快速识别出这三类角
掌握平行线的判定方法以及其他两个判定平行的条件，并将其熟练地应用于平行线的判定与证明当中去
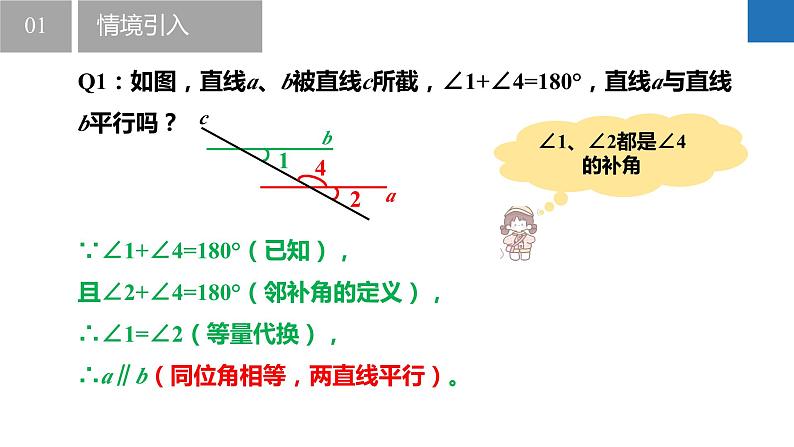
Q1：如图，直线a、b被直线c所截，∠1+∠4=180°，直线a与直线b平行吗？
∵∠1+∠4=180°（已知），且∠2+∠4=180°（邻补角的定义），∴∠1=∠2（等量代换），∴a∥b（同位角相等，两直线平行）。
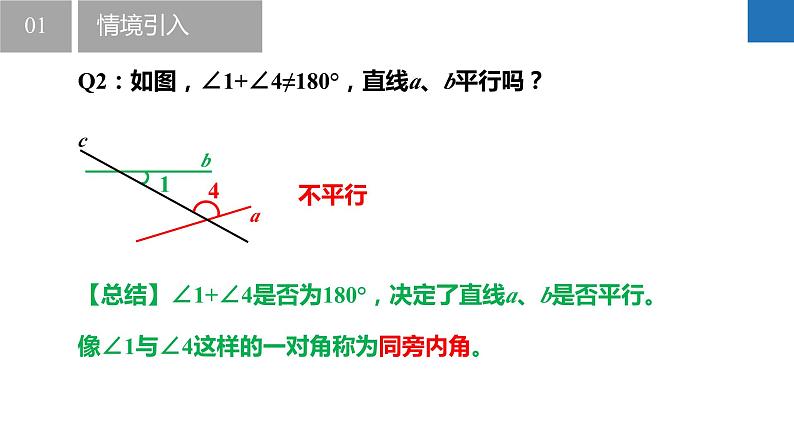
Q2：如图，∠1+∠4≠180°，直线a、b平行吗？
【总结】∠1+∠4是否为180°，决定了直线a、b是否平行。
像∠1与∠4这样的一对角称为同旁内角。
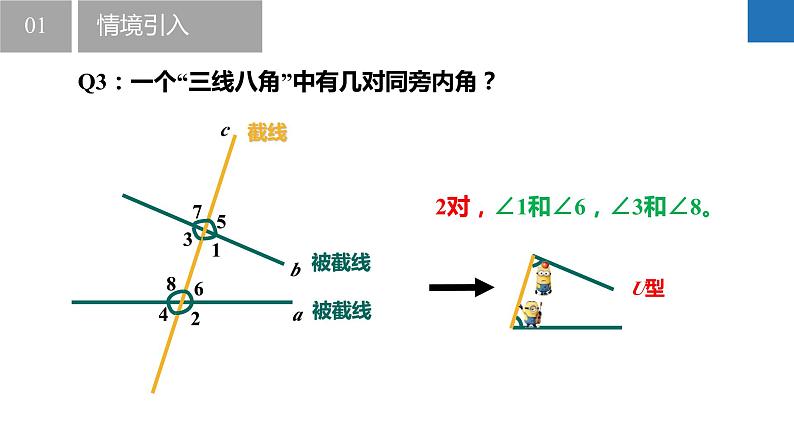
Q3：一个“三线八角”中有几对同旁内角？
2对，∠1和∠6，∠3和∠8。
Q4：同旁内角与被截线、截线之间有何位置关系？
同旁内角在被截线内侧，截线同侧。
【同旁内角的概念】在被截线内侧，且在截线同侧的两个角。一个三线八角模型中有2对同旁内角。
【三线八角模型】一个三线八角模型中有4对同位角；一个三线八角模型中有2对内错角；一个三线八角模型中有2对同旁内角。
【平行线的判定（三）】两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行。简记：同旁内角互补，两直线平行。
【符号语言】∵∠1+∠4=180°（已知），∴a∥b（同旁内角互补，两直线平行）。
【平行线的判定方法】同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行。
例1、如图，∠1和∠2不是同旁内角的是（　　）A． B．C． D．
【分析】同旁内角在被截线内侧，截线同侧。
例2、如图，直线AD、BE被直线BF和AC所截，下列说法正确的是（　　）A．∠3与∠4是同旁内角 B．∠2与∠5是同位角C．∠6与∠1是内错角 D．∠2与∠6是同旁内角
例3、若∠1与∠2是同旁内角，则（　　）A．∠1与∠2不可能相等 B．∠1与∠2一定互补C．∠1与∠2可能互余 D．∠1与∠2一定相等
【分析】不要把“同旁内角”与“互补”画上等号！
例4、如图，直线EF交AB于G，交CD于M。(1)图中有多少对同位角；(2)图中有多少对内错角；(3)图中有多少对同旁内角。
【分析1】如图，一个完整的三线八角模型，有4对同位角，2对内错角，2对同旁内角。
【分析2】如图，这个残缺的三线八角模型，有2对同位角：∠EGH与∠EMD，∠DMF与∠HGF；有1对内错角：∠CMG和∠HGM；有1对同旁内角：∠DMG与∠HGM。
【分析3】如图，这个残缺的三线八角模型，有2对同位角：∠AGE与∠NME，∠NMF与∠AGF；有1对内错角：∠NMG和∠BGM；有1对同旁内角：∠AGM与∠NMG。
【分析4】如图，这个残缺的三线八角模型，有1对内错角：∠NMG和∠HGM。
综上，图中有8对同位角，图中有5对内错角，图中有4对同旁内角。
例5、如图，下列条件中，能判断AD∥BE的是（　　）A．∠B=∠DCEB．∠1=∠3C．∠B+∠BCD=180°D．∠B+∠BAD=180°
【分析】A．∠B=∠DCE→AB∥CD；B．∠1=∠3→AB∥CD；C．∠B+∠BCD=180°→AB∥CD；D．∠B+∠BAD=180°→AD∥BE。
例6、已知：如图，BE平分∠ABD，DE平分∠BDC，且∠1+∠2=90°，求证：AB∥CD。
证明：∵DE平分∠BDC（已知），∴∠BDC=2∠1（角平分线的定义）．同理：∠ABD=2∠2（角平分线的定义），∴∠BDC+∠ABD=2∠1+2∠2=2(∠1+∠2)（等式的性质），∵∠1+∠2=90°（已知），∴∠ABD+∠BDC=180°（等量代换），∴AB∥CD（同旁内角互补，两直线平行）。
其他两个判定平行的条件
Q1：若a∥b，b∥c，则直线a与直线c有什么关系？
【总结】平行于同一条直线的两直线平行。
Q2：若a⊥b，b⊥c，则直线a与直线c有什么关系？
若在同一平面内，则a∥c
若没有“在同一平面内”这一前提，则a∥c或a与c异面
【总结】在同一平面内，垂直于同一条直线的两直线平行。
其他判定平行的两个条件
【其他判定平行的两个条件】平行于同一条直线的两直线平行；在同一平面内，垂直于同一条直线的两直线平行。
【符号语言】若a∥b，b∥c，则a∥c；在同一平面内，若a⊥b，b⊥c，则a∥c。
例1、下列命题中是真命题的是（　　）A．同位角相等B．平行于同一条直线的两直线平行C．垂直于同一条直线的两直线平行D．过一点作已知直线的平行线，有且只有一条
【分析】A、同位角不一定相等；C、在同一平面内，垂直于同一条直线的两直线平行；D、过直线外一点作已知直线的平行线，有且只有一条。
例2、画出的直线a与b不一定平行的是（　　）A． B．C． D．
【分析】 B．在同一平面内，垂直于同一条直线的两直线平行；D．同位角相等，两直线平行。
例3、如图，∠BEC=∠B+∠C，求证：AB∥CD。
证明：如图，作∠FEB=∠B，
∵∠FEB=∠B（已知），∴AB∥EF（ 内错角相等，两直线平行），又∵∠BEC=∠B+∠C=∠FEB+∠FEC（已知），∴∠FEB+∠C=∠FEB+∠FEC，即∠C=∠FEC（等量代换），∴EF∥CD（ 内错角相等，两直线平行），∴AB∥CD（平行于同一条直线的两直线平行）。
【同旁内角的概念】在被截线内侧，且在截线同侧的两个角。