数学九年级下册26.3 实践与探索说课课件ppt

这是一份数学九年级下册26.3 实践与探索说课课件ppt，共26页。PPT课件主要包含了复习引入，x≤2，导入新课，0-6，x＜-6或x＞1，x-1，合作探究，探究归纳，或x1h，典例精析等内容，欢迎下载使用。
1. 已知一次函数 y = ax + b 的图象经过 A(2，0)，B(0，-1) 两点，则关于 x 的一元一次方程 ax + b = 0 的解为_______；关于 x 的一元一次不等式 ax + b≤0 的解集为_________.
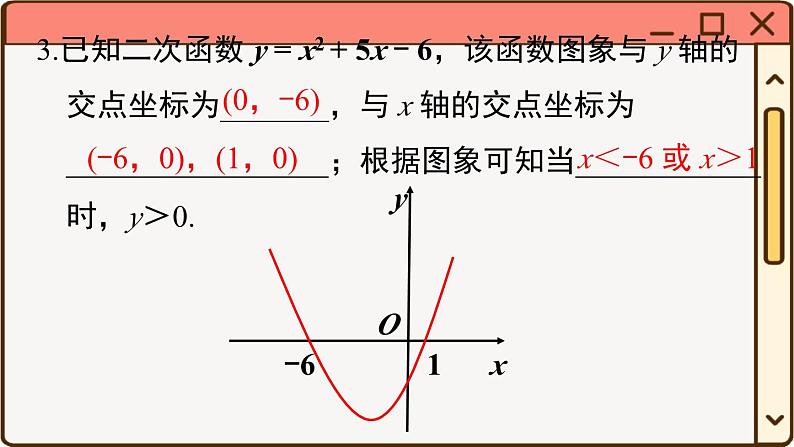
3.已知二次函数 y = x2 + 5x - 6，该函数图象与 y 轴的交点坐标为_______，与 x 轴的交点坐标为_________________；根据图象可知当____________ 时，y＞0.
(-6，0)，(1，0)
4.已知二次函数 y = ax2 + bx+ c 的图象如图所示，则一元二次方程 ax2 + bx+ c = 0 的解为_____________；当 时 y＜0；当_______时 y 随 x 的增大而减小.
x1 = -4，x2 = 2
x < -4 或 x > 2
通过观察以下图象，一元二次方程 ax2 + bx+ c = 0 的解是_______________.
二次函数 y = ax2 + bx+ c 的图象如图所示：
x1 = k1，x2 = k2
二次函数的图象与 x 轴的交点.
利用两个函数图象求方程或方程组的解
问题1 二次函数 y = ax2 + bx+ c 的图象与 x 轴 (直线 y = 0) 的交点的横坐标是一元二次方程 ax2 + bx+ c = 0 的根，那么二次函数 y = ax2 + bx + c 与直线 y = h 的交点的横坐标是否也是某一个一元二次方程的根呢？
A (x1，ax2 + bx+ c)
思考：点 A 的坐标有几种表示方式？
答：是方程 ax2 + bx + c = h 的实数根.
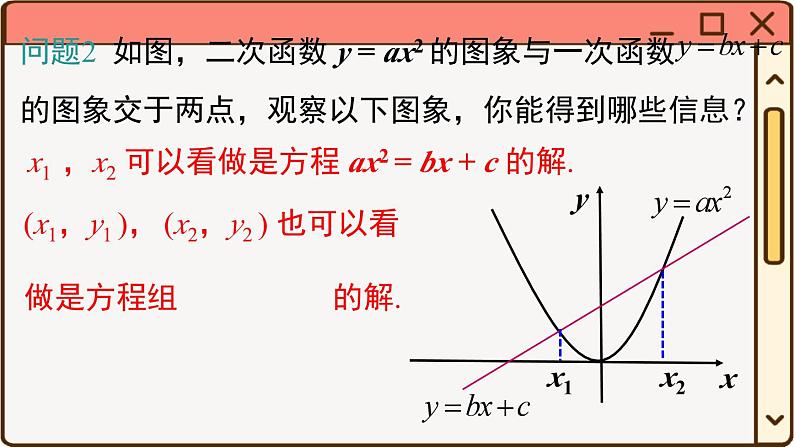
x1 ，x2 可以看做是方程 ax2 = bx + c 的解.
例1 利用二次函数的图象求一元二次方程 x2 + 2x - 1 = 3 的近似根.
解：① 原方程可变形为x2 + 2x - 4 = 0；
③观察估计抛物线 y = x2 + 2x - 4 和 x 轴的交点的横坐标.
② 用描点法作二次函数 y = x2 + 2x - 4 的图象；
y = x2 + 2x - 4
由图象可知，它们有两个交点，其横坐标一个在 -4 与 -3 之间，另一个在 1 与 2 之间，分别约为 -3.2 和 1.2.
④ 由此可知，一元二次方程 x2 + 2x - 1 = 3 的近似根为：x1≈3.2，x2≈1.2.
想一想：还有没有别的办法求这个方程的近似根？
① 用描点法作二次函数 y = x2 + 2x - 1 的图象；
③ 观察估计抛物线 y = x2 + 2x - 1 和直线 y = 3 的交点的横坐标；
② 作直线 y = 3；
y=x2+2x-4
由图象可知，它们有两个交点，其横坐标一个在 -4 与 -3 之间，另一个在 1 与 2 之间，分别约为 -3.2 和 1.2.
④ 由此可知，一元二次方程 x2 + 2x - 1 = 3 的近似根为 x1≈3.2，x2≈1.2.
① 作二次函数 y = x2 的图象；
② 作一次函数 y = -2x + 4 的图象；
③ 观察估计抛物线 y = x2 和直线 y = -2x + 4 的交点的横坐标；
由图象可知，它们有两个交点，其横坐标一个在 -4 与 -3 之间，另一个在 1 与 2 之间，分别约为 -3.2 和 1.2.
两个函数图象的交点坐标就是对应函数表达式所组成的方程组的解.
函数表达式对应方程的根，就是该函数图象与 x 轴交点的横坐标；
分析：根据题目提供的条件，无法求出抛物线的表达式.因此，我们可以换一个思路，利用函数的图象来判求不等式的解集.
利用两个函数图象求不等式的解集
解：根据题目提供的条件，画出草图：
1.若二次函数 y = x2 + bx 的图象的对称轴是经过点(2，0) 且平行于 y 轴的直线，则关于 x 的方程 x2 + bx = 5 的解为 ( ) A. x1 = 0，x2 = 4 B. x1 = 1，x2 = 5 C. x1 = 1，x2 = -5 D. x1 = -1，x2 = 5
2.若二次函数 y = ax2 + bx + c (a＜0) 的图象经过点 (2，0)，且其对称轴为 x = -1，则使函数值 y＞0 成立的 x 的取值范围是( ) A. x＜-4 或 x＞2 B. -4≤x≤2 C. x≤-4 或 x≥2 D. -4＜x＜2
3.二次函数 y = ax2 + bx + c (a ≠ 0，a，b，c 为常数)的图象如图所示，则方程 ax2 + bx + c = m 有实数根的条件是( ) A. m≥-2 B. m≥5 C. m≥0 D. m≥4
解析：方程 ax2 + bx + c = m 有实数根，即表示二次函数 y = ax2 + bx + c 的图象与直线 y = m 有交点.
解：y1 = kx + 1 经过点 A(1，0)，则 0 = k + 1，解得 k = -1.y2 = ax2 + bx - 2 经过点 A(1，0)，则 0 = a + b - 2 ①.抛物线的对称轴是 ，故 ②，联立①②，解得
4. 如图，一次函数 y1= kx + 1 与二次函数 y2 = ax2 + bx - 2 交于 A、B 两点，且 A (1，0)，抛物线的对称轴是 (1) 求 k 和 a、b 的值；
(2) 求不等式 kx + 1＞ax2 + bx - 2 的解集.
解：解方程 -x + 1 = x2 + x - 2，得 x1 = -6，x2 = 1.∴ 点 B 的横坐标为 -6.根据图象可以看出，kx + 1＞ax2 + bx - 2 的解集为 -6＜x＜1.