








- 26.2.7求二次函数的表达式 第7课时 课件+教学设计 课件 4 次下载
- 26.3.1 实践与探索 课件+教学设计 课件 3 次下载
- 27.1.1 圆的基本认识 课件+教学设计 课件 3 次下载
- 27.1.2 圆的对称性 课件+教学设计 课件 4 次下载
- 27.2.1 点与圆的位置关系 课件+教学设计 课件 4 次下载
初中数学华师大版九年级下册26.3 实践与探索获奖教学课件ppt
展开亲爱的同学们,上节课我们学习了二次函数的实践与探索,请同学们回忆一下怎样用二次函数的求解析式,基本步骤是什么?
我们常会遇到与二次函数及其图象与一元二次方程有关的问题,请与同伴共同研究,尝试解决下面的问题。
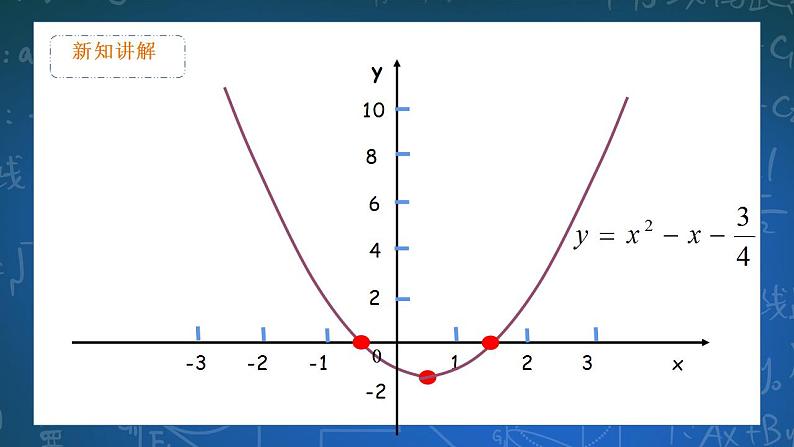
画出函数 的图象,根据图象回答下列问题:(1)图象与x轴交点的坐标是什么?
(1)由图象可知,它与x轴的交点坐标为
(2)当x取何值时y=0?这里x的取值与方程有什么关系?(3)你能从中得到什么启发?
(2)由(1)可知:当 时,y=0;解这个一元二 次方程可知:这里的x的值是一元二次方程的两个根.(3)二次函数与x轴交点的横坐标即为对应的一元二次方程的解。
根据上述问题3 画出的图象,继续回答下列问题:(1)当x取何值时,y<0?当x取何值时,y>0?(2)试用含有x的不等式来描述问题(1)。
通过解答以上问题,想一想,二次函数与一元二次方程与一元二次不等式有什么联系?
育才中学九年级(3) 班的学生在上节课的练习中出现了争 论求方程 的解时,几乎所有学生都是将方程化为 ,画出函数的图象,观察它与x轴的交点,得出方程的根.唯独小刘没有将方程移项,而是分别画出了函数 的图象如图。
认为它们的交点A、B的横坐标 就是原方程的根。对于小刘提出的解法,同学们展开了热烈的讨论。
你对这两种解法有什么看法, 请与你的同伴交流!
运用小刘的方法求下列方程的根,并检验小刘的方法是否合理。(1)x2+x-1=0(精确到0.1)(2)2x2-3x-2=0
(1)x2+x-1=0(精确到0.1)
由图象可知:方程的根为x1=0.6 x2=-1.6
(2)2x2-3x-2=0
由图象可知:方程的根为x1=2 x2=
函数y=ax2+bx+c与直线y=kx+d的交点,所以在画图像的时候,先画出函数y=ax2+bx+c,再画出直线图象,而直线与曲线的交点,便是方程的根。
用二次函数图象解一元二次方程的方法:
利用二次函数的图象求一元二次方程x2+2x-10=x+3的近似根.
(2)用描点法作一次函数y=x+3的图象
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在3与4之间,分别约为-4.2和3.2。
(3)确定方程x2+2x-10=x+3的解;
由此可知,方程x2+2x-10=x+3的近似根为:x1≈-4.2,x2≈3.2.
解:(1)用描点法作二次函数y=x2+2x-10的图象
如图,抛物线y=ax2+bx+c的对称轴是直线 x=-1,由图象知,关于x的方程ax2+bx+c=0的两个根分别是x1=1.3 ,x2=___
一般地,关于x的一元二次方程ax2+bx+c=0(a≠0)的根就是二次函数y=ax2+bx+c(a≠0)的值为0时自变量x的值,也就是函数y=ax2+bx+c的图象与x轴交点的横坐标。 在函数问题中,往往需要解方程:反过来也可以利用函数图象解方程。 函数y=ax2+bx+c与直线y=kx+d的交点,所以在画图像的时候,先画出函数y=ax2+bx+c,再画出直线图像,而直线与曲线的交点,便是方程的根。
26.3.2 实践与探索1、二次函数的应用2、用二次函数解一元二次方程
初中数学26.3 实践与探索精品ppt课件: 这是一份初中数学26.3 实践与探索精品ppt课件,共23页。PPT课件主要包含了复习引入,x≤2,0-6,x-6或x1,x1-4x22,x-4或x2,x-1,合作探究,x2h,方法二等内容,欢迎下载使用。
初中数学26.3 实践与探索一等奖课件ppt: 这是一份初中数学26.3 实践与探索一等奖课件ppt,文件包含263实践与探索1课件pptx、263实践与探索1教案docx等2份课件配套教学资源,其中PPT共32页, 欢迎下载使用。
数学26.3 实践与探索教学ppt课件: 这是一份数学26.3 实践与探索教学ppt课件,共6页。PPT课件主要包含了问题3等内容,欢迎下载使用。














