华师大数学九年级下册 小结与复习 PPT课件

这是一份华师大数学九年级下册 小结与复习 PPT课件，共34页。
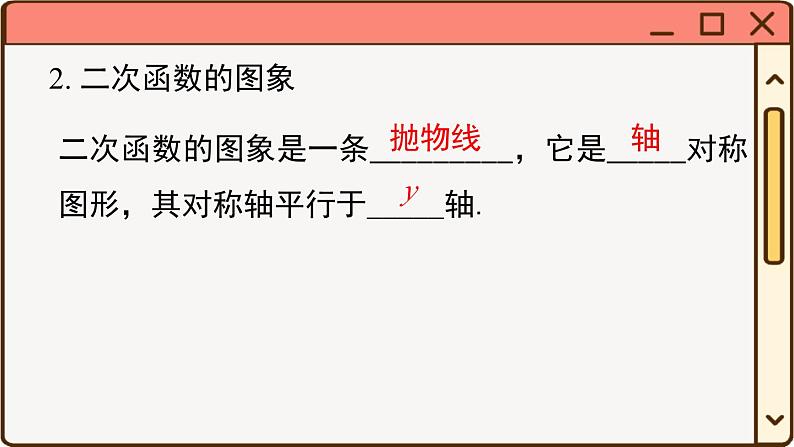
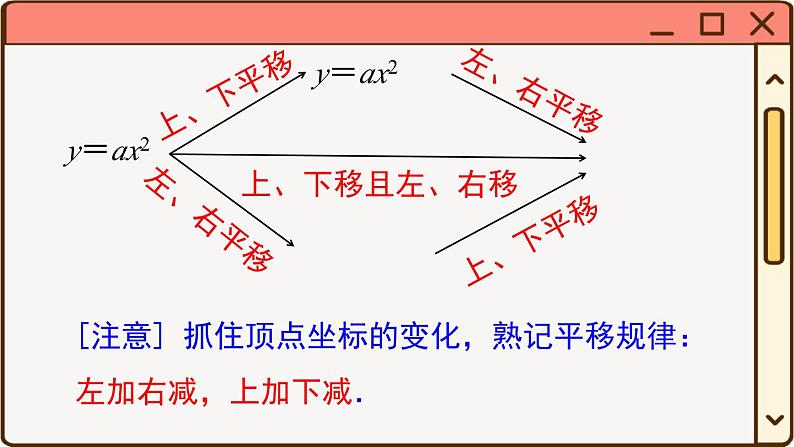
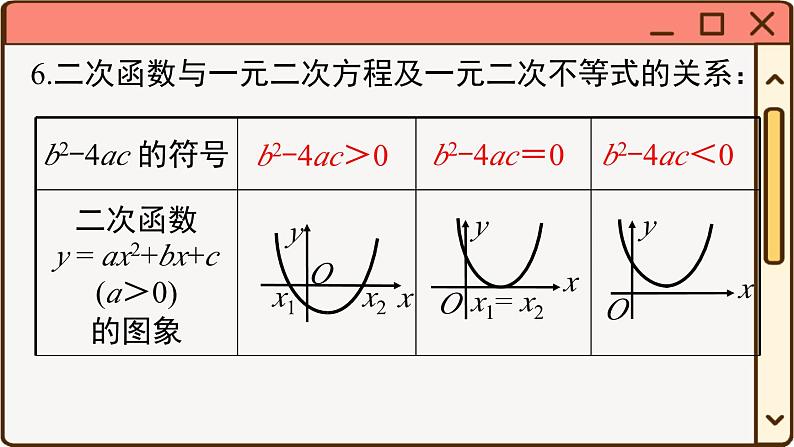
小结与复习1. 二次函数的概念一般地，形如　 (a，b，c是常数，　 　)的函数，叫做二次函数．y＝ax2＋bx＋ca ≠ 0[注意] (1) 等号右边必须是整式；(2) 自变量的最高次数是 2；(3) 当 b＝0，c＝0 时，y＝ax2 是特殊的二次函数．要点梳理2. 二次函数的图象二次函数的图象是一条　 ，它是　 对称图形，其对称轴平行于_____轴.抛物线 轴 y (1) 一般式：____________________；3. 二次函数的表达式y = ax2 + bx + c (a≠0)(2) 顶点式：____________________；y = a(x - h)2 + k (a≠0)(3) 交点式： .y = a(x - x1)(x - x2) (a≠0)4. 二次函数的平移一般地，平移二次函数 y＝ax2 的图象可得到二次函数 y＝a(x－h)2＋k 的图象．y＝ax2[注意] 抓住顶点坐标的变化，熟记平移规律：左加右减，上加下减．5. 二次函数的图象与性质：a＞0 时开口向上a＜0 时开口向下x = h(h，k)y最小 = ky最大 = k在对称轴左边 x↗y↗，在对称轴右边 x↗y↘ 在对称轴左边 x↗y↘ ，在对称轴右边x↗y↗6.二次函数与一元二次方程及一元二次不等式的关系：x2x1xyOOx1= x2xyOyxb2-4ac＞0b2-4ac＝0b2-4ac＜0x1，x2x1 = x2 =没有实数根x＜x1 或 x＞x2x ≠ x1的一切实数全体实数x1＜x＜x2无解无解例1 抛物线 y＝x2－2x＋3 的顶点坐标为_______．【解析】方法一：配方，得 y＝x2－2x＋3＝(x－1)2＋2， 则顶点坐标为 (1，2)．方法二：代入公式 ， ， 则顶点坐标为(1，2)．(1，2)考点讲练 解决此类题目可以先把二次函数 y＝ax2＋bx＋c 配方为顶点式 y＝a(x－h)2＋k 的形式，得到其对称轴是直线 x＝h，顶点坐标为 (h，k)，当自变量范围没有限制时，其最值为 y＝k；也可以直接利用公式求解.1. 对于 y＝2(x－3)2＋2 的图象，下列叙述正确的是 (　 )A. 顶点坐标为 (－3，2) B. 对称轴为 y＝3C. 当 x≥3 时，y 随 x 的增大而增大 D. 当 x≥3 时，y 随 x 的增大而减小C例2 二次函数 y＝-x2＋bx＋c 的图象如图所示，若点 A(x1，y1)，B(x2，y2) 在此函数图象上，且 x1＜x2＜1，则 y1 与 y2 的大小关系是 (　)A. y1≤y2 B. y1＜y2 C. y1≤y2 D. y1＞y2【解析】由图象看出，抛物线开口向下，对称轴是 x＝1，当 x＜1时，y 随 x 的增大而增大. ∵ x1＜x2＜1，∴ y1＜y2. B 当二次函数的表达式与已知点的坐标中含有未知字母时，可以用如下方法比较函数值的大小：(1) 用含有未知字母的代数式表示各函数值，然后进行比较；(2) 在相应的范围内取未知字母的特殊值，采用特殊值法求解；(3) 根据二次函数的性质，结合函数图象比较.2. 下列函数中，当 x＞0 时，y 值随 x 值增大而减小的是（ ） A. y = x2 B. y = x - 1 C. D. y = -3x2 D例3 已知二次函数 y＝ax2＋bx＋c 的图象如图所示，下列结论：①abc＞0；②2a－b＜0；③4a－2b＋c＜0；④(a＋c)2＜b2. 其中正确的个数是 (　)A．1　　　 B．2　　　　　C．3　　　 D．4①abc＞0解析：由图象开口向下可得 a＜0，由对称轴在 y 轴左侧可得 b＜0，由图象与 y 轴交于正半轴可得 c＞0， 则 abc＞0，故①正确.②2a－b＜0由对称轴 x＞－1 可得 2a－b＜0，故②正确.由图象上横坐标为 x＝1的点在第四象限得 a＋b＋c＜0，由图象上横坐标为 x＝－1的点在第二象限得a－b＋c＞0，则 (a＋b＋c)(a－b＋c)＜0，即 (a＋c)2－b2＜0，所以 (a＋c)2＜b2，故④正确. 故选 D.④(a＋c)2＜b2③4a－2b＋c＜0由图象上横坐标为 x＝－2 的点在第三象限可得 4a－2b＋c＜0，故③正确1. 可根据对称轴的位置确定 b 的符号： b＝0 ⇔ 对称轴是 y 轴； a、b 同号 ⇔ 对称轴在 y 轴左侧； a、b 异号 ⇔ 对称轴在 y 轴右侧. 这个规律可简记为“左同右异”.2. 当 x＝1 时，函数值 y＝a＋b＋c，当图象上横坐标 x＝1 的点在 x 轴上方时，a＋b＋c＞0；当图象上横坐标 x＝1 的点在 x 轴上时，a＋b＋c＝0；当图象上横坐标 x＝1 的点在 x 轴下方时，a＋b＋c＜0. 同理，可由图象上横坐标 x＝－1，±2 的点判断 a－b＋c，4a±b＋c 的符号.3. 已知二次函数 y =－x2＋2bx＋c，当 x＞1 时，y 的值随 x 值的增大而减小，则实数 b 的取值范围是 ( ) A. b≥－1 B. b≤－1 C. b≥1 D. b≤1D∴ b≤1. 如图所示. 例4 将抛物线 y＝x2－6x＋5 向上平移 2 个单位长度，再向右平移 1 个单位长度后，得到的抛物线解析式是 (　 )A．y＝(x－4)2－6 B．y＝(x－4)2－2C．y＝(x－2)2－2 D．y＝(x－1)2－5B【解析】因为 y＝x2－6x＋5＝(x－3)2－4，所以向上平移 2 个单位长度，再向右平移 1 个单位长度后，得到的解析式为 y＝(x－3－1)2－4＋2，即 y＝(x－4)2－2. 故选 B.4. 若抛物线 y =－7(x + 4)2－1 平移得到 y =－7x2，则可以（ ）A. 先向左平移 4 个单位，再向下平移 1 个单位B. 先向右平移 4 个单位，再向上平移 1 个单位C. 先向左平移 1 个单位，再向下平移 4 个单位D. 先向右平移 1 个单位，再向下平移 4 个单位B例5 已知关于 x 的二次函数，当 x = -1 时，函数值为 10；当 x = 1 时，函数值为 4；当 x = 2 时，函数值为 7.求这个二次函数的表达式.解：设所求的二次函数为 y = ax2 + bx + c，由题意得解得 a = 2，b = -3，c = 5.∴ 所求的二次函数表达式为 y = 2x2 - 3x + 5.1. 若已知图象上的任意三个点，则设一般式求表达式；2. 若已知抛物线的顶点坐标或对称轴与最值时，则可设顶点式求表达式，最后化为一般式；3. 若已知二次函数图象与 x 轴的交点坐标为 (x1，0)、(x2，0) 时，可设交点式求表达式，最后化为一般式.5. 已知抛物线 y = ax2 + bx + c 与抛物线 y =－x2－3x + 7 的形状相同，顶点在直线 x = 1 上，且顶点到 x 轴的距离为 5，请写出满足此条件的抛物线的表达式.解：由题意，得 a = ±1. 又∵ 顶点在直线 x = 1 上，且到 x 轴的距离为 5，∴ 顶点为 (1，5) 或 (1，－5). ∴ 表达式可为： (1) y = (x－1)2 + 5； (2) y = (x－1)2－5； (3) y =－(x－1)2 + 5；(4) y =－(x－1)2－5.例6 若二次函数 y = x2 + mx 的对称轴是 x = 3，则关于 x 的方程 x2 + mx = 7 的解为（　　）A．x1 = 0，x2 = 6 B．x1 = 1，x2 = 7 C．x1 = 1，x2 = -7 D．x1 = -1，x2 = 7D解析：∵二次函数 y = x2 + mx 的对称轴是 x = 3， ∴ = 3，解得 m = －6.∴ 关于 x 的方程 x2 + mx = 7 可化为 x2－6x－7 = 0， 即 (x + 1)(x－7) = 0，解得 x1 = －1，x2 = 7． 故选 D．例7 某广告公司设计一幅周长为 12 m 的矩形广告牌，广告设计费用每平方米 1000 元，设矩形的一边长为 x (m)，面积为 S (m2). (1) 写出 S 与 x 之间的关系式，并写出自变量 x 的取值范围；解：设矩形一边长为 x，则另一边长为 (6 - x)，∴ S = x(6 - x) = -x2 + 6x，其中 0＜x＜6. (2) 请你设计一个方案，使获得的设计费最多，并求出这个费用.S = -x2 + 6x = -(x - 3)2 + 9，∴ 当 x = 3 时，即矩形的一边长为 3 m 时， 矩形面积最大，为 9 m2.这时设计费最多，为 9×1000 = 9000 (元). 二次函数图象画法抛物线的开口方向抛物线的顶点坐标和对称轴二次函数的性质抛物线的平移最值确定表达式 应用课堂小结