







初中数学华师大版九年级下册第26章 二次函数26.3 实践与探索优质教学课件ppt
展开亲爱的同学们,上节课我们学习了二次函数的表达式,请同学们回忆一下用待定系数法求二次函数的表达式,基本步骤是什么?
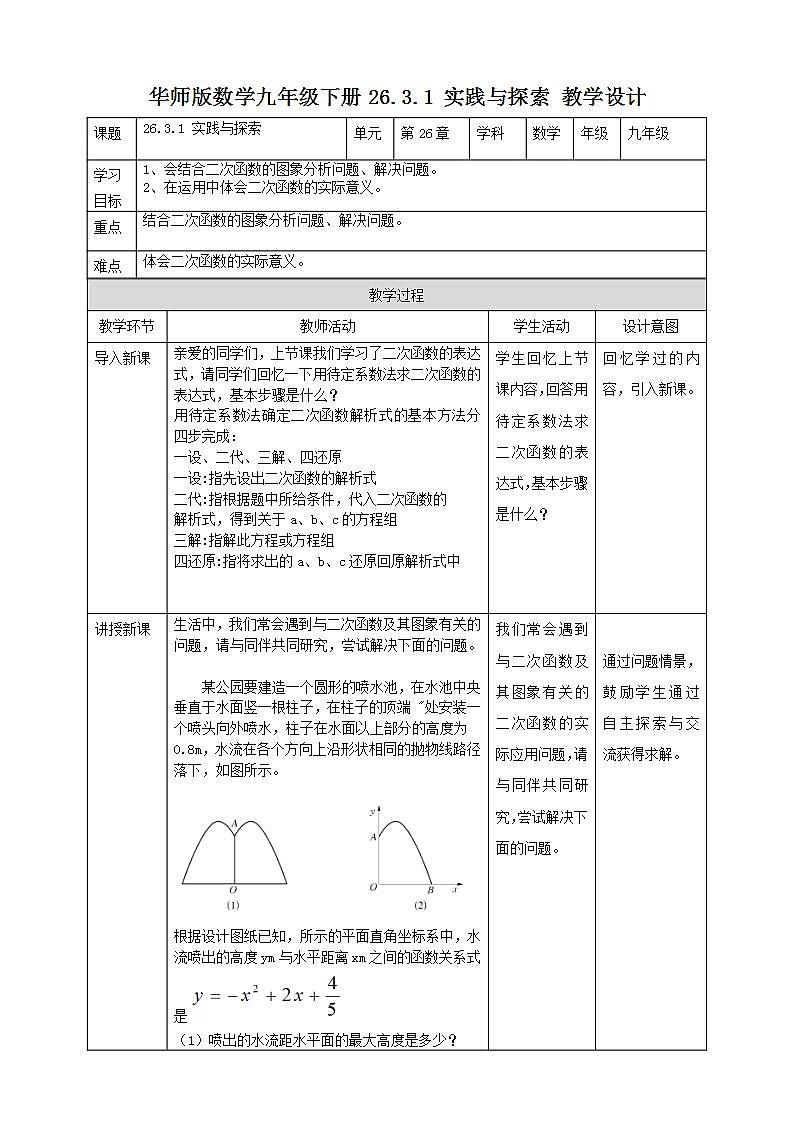
用待定系数法确定二次函数解析式的基本方法分四步完成:一设、二代、三解、四还原
一设:指先设出二次函数的解析式
二代:指根据题中所给条件,代入二次函数的解析式,得到关于a、b、c的方程组
三解:指解此方程或方程组
四还原:指将求出的a、b、c还原回原解析式中
请欣赏生活中抛物线的图片
生活中,我们常会遇到与二次函数及其图象有关的问题,请与同伴共同研究,尝试解决下面的问题。
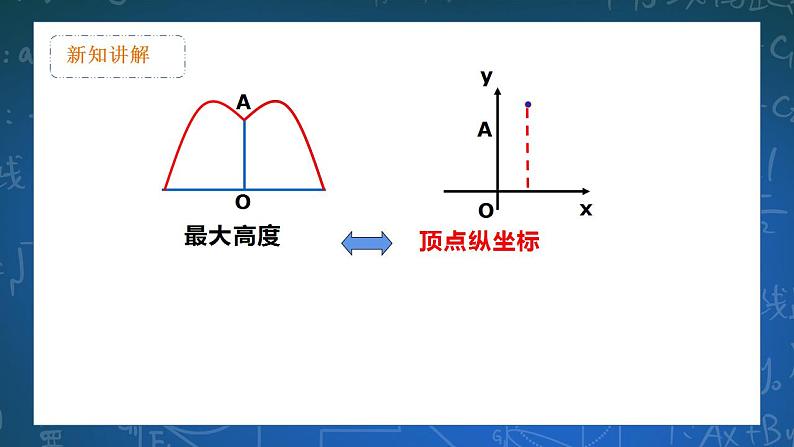
某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,在柱子的顶端 "处安装一个喷头向外喷水,柱子在水面以上部分的高度为0.8m,水流在各个方向上沿形状相同的抛物线路径落下,如图所示。
根据设计图纸已知,所示的平面直角坐标系中,水流喷出的高度ym 与水平距离xm之间的函数关系式是 (1)喷出的水流距水平面的最大高度是多少?
怎样将实际问题转化为数学问题呢?
答:喷出的水流距水平面的最大高度是1.8米。
(2)如果不计其他因素,为使水不溅落在水池外,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?
答:水池的半径至少为 米。
一个涵洞的截面边缘是抛物线,如图所示,现测得当水面宽 1.6m时,涵洞顶点与水面的距离为2.4m。这时,离开水面1.5m处,涵洞宽ED是多少?是否会超过1m?
分析,根据已知条件,要求涵洞的宽ED,只要求出FD的长度即可,即在图所示的平面直角坐标系中,求出点D的横坐标。
因为点D在涵洞截面的抛物线上,又由已知条件可得到点D的纵坐标,所以利用抛物线所对应的函数表达式可以进一步算出点D 的横坐标。你会求吗?
解:∵抛物线y=ax2(a<0)
点B在抛物线上,将B(0.8,-2.4)代入y=ax2(a<0),
再由条件设D点坐标为(x,-0.9)
∴x<0.5,2x<1
所以涵洞ED不超过1m.
某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由。
解:如图,以AB所在的直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系.
∴A(-2,0) B(2,0)
设抛物线所表示的二次函数为
∵抛物线过A(-2,0)
∴抛物线所表示的二次函数为
∴汽车能顺利经过大门.
一名男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系式是 铅球运行路线如图.(1)求铅球推出的水平距离;(2)通过计算说明铅球行进高度能否达到4 m.
[解析] (1)铅球推出的水平距离就是当高度y=0时x的值,所以解方程可求解.(2)用配方法求解二次函数的最值即可判断.
所以铅球推出的水平距离是10米.
∴函数有最大值,即当x=4时,y有最大值为3.∴铅球行进高度不能达到4 m.
26.3.1 实践与探索 1、二次函数的图象分析问题2、二次函数的实际意义
初中数学26.3 实践与探索精品ppt课件: 这是一份初中数学26.3 实践与探索精品ppt课件,共23页。PPT课件主要包含了复习引入,x≤2,0-6,x-6或x1,x1-4x22,x-4或x2,x-1,合作探究,x2h,方法二等内容,欢迎下载使用。
初中数学26.3 实践与探索一等奖课件ppt: 这是一份初中数学26.3 实践与探索一等奖课件ppt,文件包含263实践与探索1课件pptx、263实践与探索1教案docx等2份课件配套教学资源,其中PPT共32页, 欢迎下载使用。
数学26.3 实践与探索教学ppt课件: 这是一份数学26.3 实践与探索教学ppt课件,共6页。PPT课件主要包含了问题3等内容,欢迎下载使用。













