




高中数学人教A版 (2019)必修 第一册3.3 幂函数精品复习练习题
展开热点考题归纳
【题型一】幂函数概念
【典例分析】
1.(2023·全国·高一专题练习)下列函数既是幂函数又是奇函数的是( )
A.B.C.D.
【答案】A
【分析】利用幂函数及函数的奇偶性的定义,结合各选项进行判断即可.
【详解】对于A,由幂函数的定义知是幂函数,由题意可知的定义域为,,所以是奇函数,符合题意;故A正确;
对于B,由幂函数的定义知是幂函数,由题意可知的定义域为,,所以是偶函数,不符合题意;故B错误;
对于C,由幂函数的定义知不是幂函数,不符合题意;故C错误;
对于D,由幂函数的定义知不是幂函数,不符合题意;故D错误;故选:A.
2.(2022秋·云南西双版纳·高一西双版纳州第一中学校考期中)下列结论正确的是( )
A.幂函数的图象一定过原点 B.时,幂函数是增函数
C.幂函数的图象会出现在第四象限 D.既是二次函数,又是幂函数
【答案】B
【分析】利用幂函数的简单性质判断即可.
【详解】解:幂函数图象不一定过原点,例如,函数的图象不经过原点,故A不正确;
当时,幂函数,,在定义域内均为增函数,故B正确;
由函数的定义及幂函数在第一象限均有图象可知,幂函数的图象不会出现在第四象限,故C不正确;
函数是二次函数,但是不是幂函数,幂函数得形如,故D不正确.故选:B.
【提分秘籍】
【变式演练】
1.(2023·全国·高一专题练习)下列说法正确的是( )
A.若幂函数过点,则
B.函数表示幂函数
C.若表示递增的幂函数,则
D.幂函数的图像都过点,
【答案】AC
【分析】利用幂函数的定义、性质,逐项分析判断作答.
【详解】对于A,设,则,即,解得,,A正确;
对于B,函数不是幂函数,B错误;
对于C,是幂函数,则,解得或,
当时,在上单调递减,不符合题意,
当时,是R上的增函数,符合题意,因此,C正确;
对于D,幂函数不过点,D错误.
故选:AC
2.(2023·全国·高一专题练习)下列四个命题中真命题为( )
A.
B.函数是幂函数
C.为28的约数
D.对实数m,命题.命题.则是的必要不充分条件
【答案】ACD
【分析】利用配方法以及逻辑语概念可知A正确;由幂函数定义可知B错误;28的约数有等,可知C正确;求出使得命题成立的的取值范围,即可得出D正确.
【详解】对于A,易知,即可知对于恒成立,所以A正确;
对于B,根据幂函数定义可知幂函数的系数必须为1,而的系数为2,所以函数不是幂函数,即B错误;
对于C,易知等都是28的约数,因此为28的约数,即C正确;
对于D,若命题成立可得,解得,显然,
即,所以是的必要不充分条件,即D正确.
故选:ACD
3.(2021秋·湖北十堰·高一校联考期中)下列结论中错误的命题是( )
A.函数是幂函数
B.函数是偶函数不是奇函数
C.函数的单调递减区间是
D.有的单调函数没有最值
【答案】BC
【分析】根据幂函数的定义,函数奇偶性的判断方法,单调区间的书写形式,以及函数最值的概念,对每个选项进行逐一分析,即可判断和选择.
【详解】对A:是幂函数,故正确;
对B:的定义域为或,其关于原点对称.
又,满足且满足,
故该函数在定义域上既是奇函数,又是偶函数,故错误;
对C:函数有多个单调区间时,不能用“”,故错误;
对D:例如幂函数在上是单调函数,但是没有最值,故正确.
故选:BC.
【题型二】幂函数解析式
【典例分析】
1.(2023春·河南开封·高二校联考期末)若幂函数的图象不经过坐标原点,则实数的取值为( )
A.B.C.-1D.1
【答案】B
【分析】根据幂函数的定义,解出或,,分别验证和时图像是否经过原点,即可得到答案.
【详解】由题意有,解得或,
①当时,,函数图象过原点,不合题意;
②当时,,函数图象不过原点,合题意.故.故选:B
2.(2022秋·山西运城·高一校考阶段练习)幂函数在上为增函数,则的取值是( )
A.或B.C.D.
【答案】C
【分析】根据函数是幂函数,由求得m,再根据函数在上为增函数,确定m的取值.
【详解】因为函数是幂函数,所以,即,
解得或,当时,,符合题意;当时,,不符合题意;
所以的取值是2,故选:C
【变式演练】
1.(2020秋·江苏无锡·高一江苏省锡山高级中学校考期中)若函数是幂函数,且图像关于原点对称,则实数m为( )
A.2B.-1C.4D.2或-1
【答案】A
【解析】根据幂函数的定义,可得,求出的值,再判断是否满足幂函数的图像关于原点对称,即可求出结果.
【详解】∵幂函数, ∴, 解得,或;
又幂函数的图像关于原点对称,∴当时,,幂函数为,满足题意;
当时, ,幂函数为,不满足题意;
综上,.故选:A.
2.(2021秋·湖北荆州·高一统考期末)已知函数是幂函数,且在上单调递减,则( )
A.0B.-1C.2D.2或-1
【答案】B
【解析】由函数是幂函数,结合函数在上单调递减,求出.
【详解】由函数是幂函数,则,解得或.
又函数在上单调递减,则,即.故选:B.
3.(2022秋·四川南充·高一校考阶段练习)幂函数在为增函数,则的值为( )
A.1或3B.3C.2D.1
【答案】D
【详解】函数为 幂函数,则:,解得:,
幂函数单调递增,则:,据此可得:.
本题选择D选项.
【题型三】幂函数图像
【典例分析】
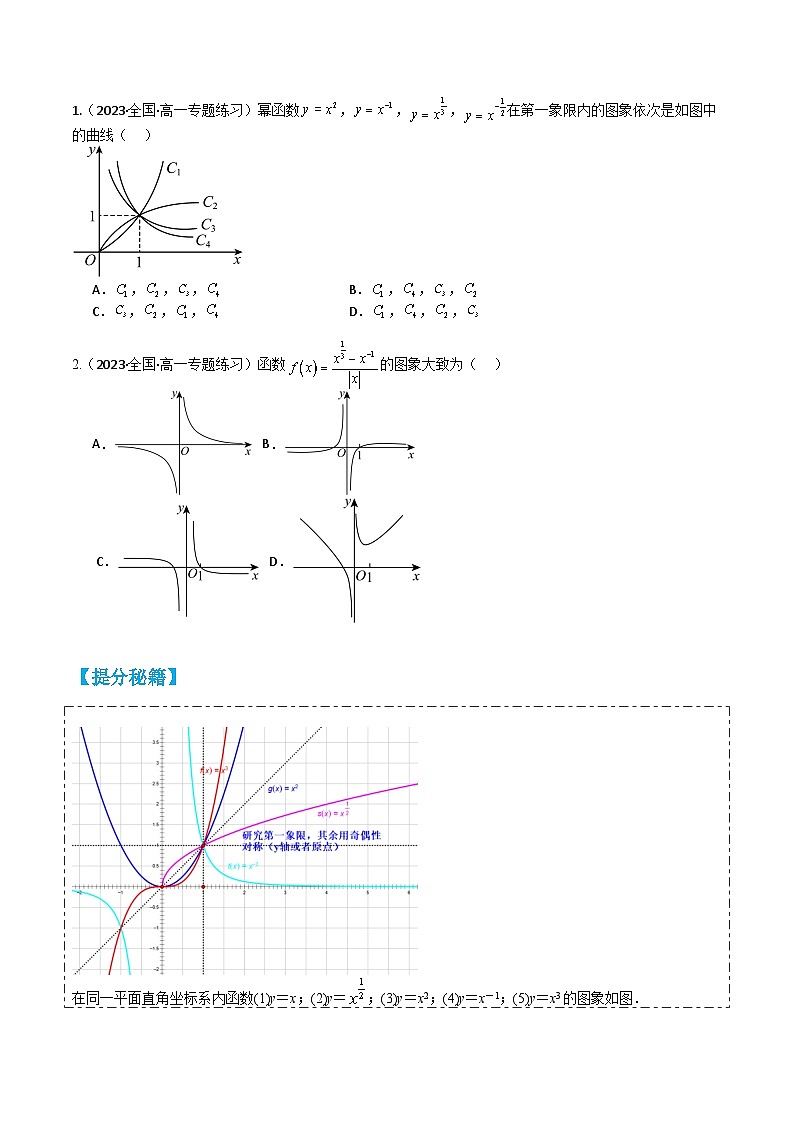
1.(2023·全国·高一专题练习)幂函数,,,在第一象限内的图象依次是如图中的曲线( )
A.,,,B.,,,
C.,,,D.,,,
【答案】D
【分析】根据幂函数的指数的大小与曲线的位置关系(可在直线右侧)比较从而得出结论.
【详解】由于在第一象限内直线的右侧,幂函数的图象从上到下相应的指数由大变小,即“指大图高”,故幂函数在第一象限内的图象为,在第一象限内的图象为,在第一象限内的图象为,在第一象限内的图象为.故选:D.
2.(2023·全国·高一专题练习)函数的图象大致为( )
A. B.
C. D.
【答案】B
【分析】利用特殊值法即可排除错误选项.
【详解】由,排除A,D,
当时,,所以,排除C.故选:B.
【提分秘籍】
【变式演练】
1.(2023·全国·高一专题练习)给定一组函数解析式:
①;②;③;④;⑤;⑥;⑦.
如图所示一组函数图象.图象对应的解析式号码顺序正确的是( )
A.⑥③④②⑦①⑤B.⑥④②③⑦①⑤
C.⑥④③②⑦①⑤D.⑥④③②⑦⑤①
【答案】C
【分析】根据幂函数的图象的性质判断各图象对应解析式的形式,即可得答案.
【详解】图象(1)关于原点对称,为奇函数,且不过原点、第一象限递减,故满足;
图象(2)关于轴对称,为偶函数,且不过原点、第一象限递减,故满足;
图象(3)非奇非偶函数,且不过原点、第一象限递减,故满足;
图象(4)关于轴对称,为偶函数,且过原点、第一象限递增,故满足;
图象(5)关于原点对称,为奇函数,且过原点、第一象限递增,故满足;
图象(6)非奇非偶函数,且过原点、第一象限递增,而增长率随增大递减,故满足;
图象(7)非奇非偶函数,且过原点、第一象限递增,而增长率随增大递增,故满足;
故图象对应解析式顺序为⑥④③②⑦①⑤.
故选:C
2.(2023·全国·高一专题练习)已知幂函数(且p与q互质)的图像如图所示,则( )
A.p、q均为奇数且B.p为奇数,q为偶数且
C.p为奇数,q为偶数且D.p为偶数,q为奇数且
【答案】D
【分析】根据图像的对称性及形状结合幂函数的图像特征可直接解答.
【详解】由图像知函数为偶函数,所以p为偶数,且由图像的形状判定,
又因为p与q互质,所以q为奇数,
故选:D.
3.(2023·全国·高一专题练习)如图,下列3个幂函数的图象,则其图象对应的函数可能是( )
A.①,②,③B.①,②,③
C.①,②,③D.①,②,③
【答案】A
【分析】根据幂函数的图象与性质,逐个判定,即可求解.
【详解】由函数是反比例函数,其对应图象为①;
函数的定义域为,应为图②;
因为的定义域为且为奇函数,故应为图③.
故选:A.
【题型四】幂函数求值
【典例分析】
1.(2022秋·安徽·高二淮南第二中学校联考开学考试)已知幂函数在上单调递增,则( )
A.B.2C.D.32
【答案】D
【分析】根据幂函数的定义及单调性,求出函数的解析式,再求函数值即可.
【详解】因为是幂函数,
所以,即,解得,或,
当时,在上单调递减,不满足题意;
当时,在上单调递增,满足题意,所以幂函数的解析式为.所以.故选:D.
2.(2023·全国·高一专题练习)函数是幂函数,且在上单调递增,则 ( )
A.B.
C.或D.或
【答案】B
【分析】由幂函数的性质得出解析式,再求函数值.
【详解】由题意可知,,解得,.故选:B
【变式演练】
1.(2023·全国·高三专题练习)函数同时满足①对于定义域内的任意实数x,都有;②在上是减函数,则的值为( )
A.8B.4C.2D.1
【答案】B
【分析】由的值依次求出的值,然后根据函数的性质确定,得函数解析式,计算函数值.
【详解】,,,代入分别是,
在定义域内,即是偶函数,因此取值或0,
时,在上不是减函数,
只有满足,此时,,.故选:B.
2.(2022·全国·高一专题练习)幂函数在区间上单调递增,则( )
A.27B.C.D.
【答案】A
【分析】根据幂函数的概念及性质,求得实数的值,得到幂函数的解析式,即可求解.
【详解】由题意,令,即,解得或,
当时,可得函数,此时函数在上单调递增,符合题意;
当时,可得,此时函数在上单调递减,不符合题意,
即幂函数,则.故选:A.
3.(2022·高一课时练习)已知幂函数在上单调递减,则( )
A.2B.16C.D.
【答案】D
【分析】根据题意列出方程组,求得m的值,即得函数解析式,代入求值可得答案.
【详解】由题意得,解得,
所以,故,故选:D
4.(2023·江苏镇江·扬中市第二高级中学校考模拟预测)已知幂函数在上是减函数,则的值为( )
A.3B.C.1D.
【答案】C
【分析】先根据是幂函数,由求得,再根据函数在上是减函数,确定的值求解.
【详解】由函数为幂函数知,
,解得或.
∵在上是减函数,而当时,,在是增函数,不符合题意,
当时,,符合题意,
∴,,∴.故选:C.
【题型五】 幂函数定义域
【典例分析】
1.(2023·全国·高一专题练习)已知幂函数,则此函数的定义域为 .
【答案】.
【分析】根据幂函数的定义,求得,得到,进而求得函数的定义域.
【详解】由幂函数,可得,解得,即,
则满足,即幂函数的定义域为.
故答案为:.
2.(2023·全国·高一专题练习)已知幂函数的定义域为,则实数 .
【答案】1
【分析】由幂函数的定义列出方程,求出或,通过检验定义域可知满足要求.
【详解】由题意得到,解得:或,
当时,,定义域为,符合题意;
当时,,定义域为,不符合题意.
故.故答案为:1
【提分秘籍】
【变式演练】
1.(2021秋·浙江金华·高一浙江金华第一中学校考期中)函数的定义域为 .
【答案】
【分析】结合指数幂的运算性质化简表达式,即可求解
【详解】由可知其定义域为.
故答案为:
2.(2022·全国·高一专题练习)已知幂函数的定义域为,且单调递减,则 .
【答案】
【分析】根据幂函数的单调性,得到的范围,再由其定义域,根据,即可确定的值.
【详解】因为幂函数的定义域为,且单调递减,
所以,则,
又,所以的所有可能取值为,,,
当时,,其定义域为,不满足题意;
当时,,其定义域为,满足题意;
当时,,其定义域为,不满足题意;
所以.故答案为:
3.(2023·全国·高一专题练习)函数的定义域为( )
A.B.
C.D.
【答案】D
【分析】化简函数解析式,根据函数解析式有意义可得出关于的不等式组,由此可解得原函数的定义域.
【详解】因为,则,可得,
故函数的定义域为.故选:D.
【题型六】 复合型幂函数定义域
【典例分析】
1.(2023·全国·高一专题练习)函数的定义域是( )
A.B.C.D.
【答案】B
【分析】根据函数解析式有意义可得出关于实数的不等式组,由此可解得函数的定义域.
【详解】因为,
则有,解得且,因此的定义域是.故选:B.
2.(2023秋·湖南衡阳·高三校考阶段练习)函数的图像大致是( )
A.B.C.D.
【答案】A
【分析】利用时排除选项D,利用时排除选项C,利用时排除选项B,所以选项A正确.
【详解】函数的定义域为
当时,,可知选项D错误;
当时,,可知选项C错误;
当时,,可知选项B错误,选项A正确.故选:A
【变式演练】
1.(2020·高一课时练习)若函数则函数y=f(4 x-3)的定义域是( )
A.(-∞,+∞)B.
C.D.
【答案】D
【分析】先求出,根据幂函数的定义域求解即可.
【详解】幂函数,,
所以,所以,所以函数的定义域是,故选D.
2.(2023·上海·高一专题练习)若要使有意义,则取值范围是 .
【答案】
【分析】由题可得,由即得.
【详解】∵,要使有意义,则,即,
∴.故答案为:.
3.(2023·高一课时练习)已知幂函数的图象过点,则的定义域为 .
【答案】
【分析】首先求幂函数的解析式,再求函数的定义域,根据复合函数的形式,求函数的定义域.
【详解】∵的图象过点,∴,,应该满足:,即,∴的定义域为.故答案为:
【题型七】复合型幂函数单调性
【典例分析】
1.(2023秋·北京朝阳·高一统考期末)下列函数中,在其定义域上单调递增且值域为的是( )
A.B.C.D.
【答案】B
【分析】分别求出每个选项的单调性和值域即可得出答案.
【详解】对于A,在定义域上单调递增且值域为,故A不正确;
对于B,在定义域上单调递增值域为,故B正确;
对于C,由双勾函数的图象知,在上单调递增,在上单调递减,故C不正确;
对于D,的值域为,故D不正确.故选:B.
2.(2022秋·湖北省直辖县级单位·高三校考阶段练习)函数的单调递减区间为( )
A.B.
C.D.
【答案】A
【分析】先求定义域,再利用复合函数的同增异减可得函数单调递减区间.
【详解】,解得即函数的定义域为,
因为函数在定义域内是单调递增函数,要求函数的单调递减区间,
即求函数在上的单调减区间
由于其开口向下,且对称轴为,故减区间为故选:A.
【提分秘籍】
【变式演练】
1.(2023·全国·高一专题练习)函数的单调递增区间是( )
A.B.C.D.
【答案】D
【分析】求出函数的定义域,再根据复合函数的单调性即可得出答案.
【详解】解:,则或,
所以函数的定义域为,
令,此函数在上递减,在上递增,
又函数为增函数,
所以函数的单调递增区间是故选:D.
2.(2023·全国·高一专题练习)若函数满足,则的单调递增区间为
A.(-∞,2]B.(-∞,1]C.[1,+∞)D.[2,+∞)
【答案】A
【分析】因为函数满足,则函数关于对称,进而求出参数的值,进而求出函数的递增区间.
【详解】解法1:由知,函数图象关于对称,所以,=2.函数在(-∞,2]单调递减,在[2,+∞)单调递增;而在(-∞,+∞)上递减,由复合函数的单调性知,函数的单调递增区间为(一∞,2],故选A.
解法2:由函数图象变换可知,=2且函数的单调递增区间为(一∞,2].故选A.
3.(2023·江苏·高一专题练习)函数的单调增区间是 .
【答案】
【分析】求出函数的定义域,结合复合函数的单调性即可求出结果.
【详解】函数的定义域满足,解得,
故函数的定义域为
令,则,
因为函数在上单调递增,在上单调递减,
且函数在上单调递增,
结合复合函数的单调性可知函数在上单调递增,在上单调递减,
故答案为:.
【题型八】幂函数值域
【典例分析】
1.(2024·全国·高三专题练习)下列函数中,定义域和值域不相同的是( )
A.B.C.D.
【答案】D
【分析】根据一次函数、反比例函数、幂函数和分段函数的性质,逐个选项进行判断即可得到答案.
【详解】对于A:函数的定义域为,值域也为,不符合题意;
对于B:函数的定义域和值域都为,不符合题意;
对于C:的定义域和值域都为,不符合题意;
对于D:的定义域为;
当时,;当时,;
所以值域为,定义域和值域不相同,符合题意;
故选:D.
2.(2022秋·甘肃金昌·高一永昌县第一高级中学校考期中)幂函数与幂函数( )
A.定义域相同B.值域相同C.单调性相同D.是同一函数
【答案】B
【分析】求出函数定义域,根据幂函数性质性即可解决.
【详解】由题知
,定义域为,单调性递增,值域为,
,定义域为,为偶函数,单调性先减后增,值域为,
所以与值域相同,故选:B
【提分秘籍】
【变式演练】
1.(2022·全国·高三专题练习)幂函数中a的取值集合C是的子集,当幂函数的值域与定义域相同时,集合C为( )
A.B.C.D.
【答案】C
【分析】分别求出各幂函数的定义域和值域,得到答案.
【详解】当时,定义域和值域均为,符合题意;
时,定义域为,值域为,故不合题意;
时,定义域为,值域为,符合题意;
时,定义域与值域均为R,符合题意;
时,定义域为R,值域为,不符合题意;
时,定义域与值域均为R,符合题意.故选:C
2.(2023秋·全国·高一专题练习)在下列函数中,定义域和值域不同的是( )
A.B.C.D.
【答案】D
【分析】把幂函数写成根式的形式即可求出定义域及值域,逐项分析即可得解.
【详解】由可知,,,定义域、值域相同;
由可知,,定义域、值域相同;
由可知,,,定义域、值域相同;
由可知,,,定义域、值域不相同.故选:D
3.(2023·全国·高一专题练习)幂函数的图象过点,则函数的值域是( )
A.B.C.D.
【答案】C
【分析】设,带点计算可得,得到,令转化为二次函数的值域求解即可.
【详解】设,代入点得,则,令,
函数的值域是.故选:C.
【题型九】幂函数单调性解不等式
【典例分析】
1.(2023·全国·高一专题练习)已知幂函数在上单调递增,不等式的解集为( )
A.B.C.D.
【答案】B
【分析】根据幂函数的定义及性质求出的值,然后判断函数的单调性,利用单调性即可求解不等式的解集.
【详解】解:因为函数为幂函数,所以,解得或,
又幂函数在上单调递增,
所以,此时在R上单调递增,
因为,所以,解得或,
所以不等式的解集为,
故选:B.
2.(2021·高一课时练习)已知幂函数,若,则的取值范围为( )
A.B.C.D.
【答案】D
【分析】根据幂函数的单调性与定义域可解不等式.
【详解】因为幂函数的定义域为,且是定义域上的减函数,
所以若,则解得.
故选:D.
【变式演练】
1.(2021·高一课时练习)若,则不等的解集为( )
A.B.C.D.
【答案】D
【分析】由幂函数的性质可知是定义在上的增函数,再根据函数的单调性,将函数不等式转化为自变量的不等式,需注意函数的定义域;
【详解】解:由,知是定义在上的增函数,则由不等式,得,解得,所以原不等式的解集为.
故选:D.
2..(2022·全国·高一专题练习)已知是幂函数,且在上单调递增,则满足的实数的范围为( )
A.B.C.D.
【答案】D
【分析】由幂函数的定义求得的可能取值,再由单调性确定的值,得函数解析式,结合奇偶性求解.
【详解】由题意,解得或,
又在上单调递增,所以,,
所以,,易知是偶函数,
所以由得,解得或.
故选:D.
3.(2022秋·北京·高一校考期中)已知是减函数,那么实数的取值范围是( )
A.B.C.D.
【答案】A
【分析】根据分段函数的单调性列不等式组,解不等式组求得的取值范围.
【详解】由于函数是减函数,所以,解得.
故选:A.
【题型十】构造幂函数解不等式(或求参)
【典例分析】
1.(2023·全国·高一专题练习)不等式的解为( )
A.B.C.D.
【答案】D
【分析】先求出函数的定义域,单调性,且当上,恒成立,当上,恒成立,从而分三种情况,列出不等式组,求出解集.
【详解】定义域为,且在与上均为减函数,
且当上,恒成立,当上,恒成立,
故①或②或③,
解①得:,解②得:,解③得:,
综上:不等式的解为.故选:D
2.(2023·全国·高一专题练习)若,则实数的取值范围是( )
A.B.
C.D.
【答案】D
【分析】构造,通过函数单调性及定义域,列出不等式,求出取值范围.
【详解】解:由题知构造,由幂函数性质可知单调递增,
,,,
综上:.故选:D
【提分秘籍】
【变式演练】
1.(2021秋·福建三明·高一校联考期中)若,则实数a的取值范围是( )
A.[,+∞)B.(-∞,]C.(,]D.[,]
【答案】D
【分析】利用幂函数的单调性解不等式即可.
【详解】不等式可化为:
,解得:.故选:D
2.(2020秋·江苏苏州·高一统考期中)若实数m满足,则m的取值范围是( )
A.B.
C.D.
【答案】D
【分析】令函数,根据幂函数的图象与性质,求得函数定义域、单调性和奇偶性,结合,列出不等式组,即可求解.
【详解】令定义域为,且为偶函数,
根据幂函数的图象与性质,可得在区间上单调递增,在单调递增,
因为,则满足,解得,
所以实数m的取值范围是.故选:D.
3.(2020·高一单元测试)设;,则p是q成立的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】B
【分析】由题意结合幂函数的性质可转化条件得,由充分条件和必要条件的概念即可得解.
【详解】由得解得,
因为不能推出,可推出,
所以p是q成立的必要不充分条件.故选:B.
【题型十一】幂函数性质比大小
【典例分析】
1.(2023·全国·高一专题练习)设,,,则a,b,c的大小关系是( )
A.B.
C.D.
【答案】A
【分析】根据幂函数的单调性判断.
【详解】因为,,,
又,在上单调递增,
所以.综上,.故选:A.
2.(2023秋·黑龙江双鸭山·高一双鸭山一中校考阶段练习)若,,,则( )
A.B.
C.D.
【答案】B
【分析】根据构造函数,结合函数的单调性以及和“1”比较大小得出结果.
【详解】设函数,则在上单调递增,
故,即,又,即.
故选:B.
【提分秘籍】
【变式演练】
1.(2023·全国·高一专题练习)设,,,则( )
A.B.C.D.
【答案】B
【分析】根据幂函数的单调性比较大小.
【详解】构造幂函数,由该函数在定义域内单调递增,且,故
故选:B
2.(2023·全国·高一专题练习)已知,,,则a,b,c的大小关系为( )
A.B.C.D.
【答案】D
【分析】根据幂函数的单调性确定函数值大小,即可得a,b,c的大小关系.
【详解】由于幂函数在上单调递增,又,,,
,所以,则.故选:D.
3.(2023·全国·高一专题练习)已知,则( )
A.B.C.D.
【答案】B
【分析】由已知,根据题意给出的式子,先进行化简,得到,然后根据幂函数的单调性,即可做出判断.
【详解】由已知,,化简,
因为幂函数在上单调递增,而,
所以.故选:B.
1.(2023·全国·高一专题练习)下列函数是幂函数的是( )
A.B.C.D.
【答案】D
【分析】根据幂函数概念即可得解.
【详解】因为函数叫做幂函数,其中x是自变量,a是常数,
对于A,是二次函数;
对于B,是一次函数;
对于C,,由前的系数不为,故不是幂函数;
对于D,满足幂函数的概念,故是幂函数.
故选D.
2.(2021秋·高一课时练习)已知幂函数的图象过点,则幂函数的解析式为( )
A.B.
C.D.
【答案】C
【分析】设幂函数,代入点即可求解.
【详解】设幂函数,代入点,则,解得,
.故选:C.
3.(2020秋·安徽六安·高一六安一中校考阶段练习)若幂函数在单调递减,则( )
A.8B.3C.1D.
【答案】D
【分析】根据幂函数的定义和性质进行求解即可.
【详解】因为是幂函数,所以或,
当时,函数是实数集上的增函数,不符合题意;
当时,函数在单调递减,符合题意,,
故选:D
4.(2022秋·山东滨州·高一校考期中)若函数为幂函数,则( )
A.B.函数的定义域为R
C.函数是奇函数D.函数在区间上单调递减
【答案】D
【分析】根据函数为幂函数求出,然后利用幂函数的性质逐一判断即可.
【详解】因为函数为幂函数,
,解得,A错误;
,其定义域为,B错误;
,函数是偶函数,C错误
函数在区间上单调递减,D正确.
故选: D.
5.(2023·高一课时练习)若有意义,则实数的取值范围是
【答案】
【解析】直接根据负数不能开偶次方根求解.【详解】若有意义,则,
解得所以实数的取值范围是,故答案为:
6.(2023·全国·高一专题练习)幂函数,,则下列结论正确的是( )
A.B.函数是偶函数
C.D.函数的值域为
【答案】ABD
【分析】根据函数为幂函数,求得m的值,判断A;根据函数奇偶性定义可判断B;根据幂函数的单调性可判断C;根据函数解析式可求函数值域,判断D.
【详解】因为是幂函数,所以,
解得或,又因为,故,A正确;
则,定义域为,满足,故是偶函数,B正确;
为偶函数,在上单调递减,故,C错误;
函数的值域为,D正确,
故选:ABD
7..(2023·高一课时练习)用函数表示函数和中的较大者,记为:,若,,则的大致图像为( )
A.B.
C.D.
【答案】A
【分析】利用特殊值确定正确选项.
【详解】依题意,
,排除CD选项.
,排除B选项.
所以A选项正确.
故选:A
8..(2020秋·福建·高一厦门一中校考期中)已知函数的增区间为( )
A.B.C.D.
【答案】A
【解析】先求得函数的定义域,再令,结合的单调性,利用复合函数的单调性求解.
【详解】由,
解得或,
因为在递减,在递增,
又因为在递增,
所以增区间为
故选:A
9.(2023·全国·高一专题练习)已知幂函数的图象过点,且,则的取值范围是( )
A.B.C.D.
【答案】C
【解析】先根据题意得幂函数解析式为,再根据函数的单调性解不等式即可得答案.
【详解】解:因为幂函数的图像过点,
所以,所以,所以,
由于函数在上单调递增,
所以,解得:.
故的取值范围是.
故选:C.
10.(2018秋·吉林·高一吉林毓文中学校考期中)若,则实数m的取值范围是( )
A.B.C.D.
【答案】D
【解析】根据函数的单调性及定义域得到不等式,再解一元二次不等式组即可得解.
【详解】在上为增函数,
,
即故选:.
11.(2023·全国·高一专题练习)设,,,则( )
A.B.C.D.
【答案】D
【分析】通过观察三个数的特征可知,很难化成同底形式,所以可通过构造幂函数,利用其单调性即可比较得出结果.
【详解】由题意可知,,
,
因为在上是增函数,,所以.
故选:D.
12.(2020·高一课时练习)满足不等式的实数的取值范围是 .
【答案】
【分析】在同一坐标系内画出幂函数和的图象,由图象观察可得.
【详解】在同一坐标系内画出幂函数和的图象,的图象位于的图象上方,对应自变量的取值范围既是实数的取值范围,由图象得,
故答案为:.
一、热考题型归纳
【题型一】 幂函数概念
【题型二】 幂函数解析式
【题型三】 幂函数图像
【题型四】 幂函数求值
【题型五】 幂函数定义域
【题型六】 复合型幂函数定义域
【题型七】 复合型幂函数单调性
【题型八】 幂函数值域
【题型九】 幂函数单调性解不等式
【题型十】 构造幂函数解不等式(求参)
【题型十一】幂函数性质比大小
二、培优练
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
五个幂函数的性质
y=x
y=x2
y=x3
y=x-1
定义域
R
R
R
[0,+∞)
{x|x≠0}
值域
R
[0,+∞)
R
[0,+∞)
{y|y≠0}
奇偶性
奇
偶
奇
非奇非偶
奇
单调性
增
在[0,+∞) 上增,
在(-∞,0] 上减
增
增
在(0,+∞)上减,
在(-∞,0)上减
在同一平面直角坐标系内函数(1)y=x;(2)y=;(3)y=x2;(4)y=x-1;(5)y=x3的图象如图.
1.所有的幂函数在(0,+∞)上都有定义,并且图象都过点(1,1).
2.幂函数定义域,可以把幂函数转化为根式形式。
1. 当α>0时,幂函数的图象通过原点,并且在区间[0,+∞)上是增函数.特别地,当α>1时,幂函数的图象下凸;当0<α<1时,幂函数的图象上凸.
2.当α<0时,幂函数的图象在区间(0,+∞)上是减函数.
3.复合型函数,可以转化为内外函数,根据“同增异减”判定函数单调性
幂函数值域,可以借助幂函数的奇偶性,单调性,以及幂函数图像来求解
构造幂函数解不等式,构造完对应的函数后,确认对应的定义域,单调西,奇偶性,需要对函数“自变量”进行分类讨论。
此类题在构建函数模型时要注意幂函数的特点:指数不变.比较大小的问题主要是利用函数的单调性,特别是要善于应用“搭桥”法进行分组,常数0和1是常用的中间量.
高中数学人教A版 (2019)必修 第一册2.2 基本不等式精品巩固练习: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000263_t7/?tag_id=28" target="_blank">2.2 基本不等式精品巩固练习</a>,文件包含专题2-2基本不等式16种题型归类原卷版docx、专题2-2基本不等式16种题型归类解析版docx等2份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。
专题3-5 抛物线定义及性质12种题型归类(讲+练)-高二数学热点题型讲与练(人教A版选择性必修第一册): 这是一份专题3-5 抛物线定义及性质12种题型归类(讲+练)-高二数学热点题型讲与练(人教A版选择性必修第一册),文件包含专题3-5抛物线定义及性质归类原卷版docx、专题3-5抛物线定义及性质归类解析版docx等2份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。
数学选择性必修 第一册3.2 双曲线习题: 这是一份数学选择性必修 第一册3.2 双曲线习题,文件包含专题3-3双曲线性质归类原卷版docx、专题3-3双曲线性质归类解析版docx等2份试卷配套教学资源,其中试卷共54页, 欢迎下载使用。














