高中数学人教A版 (2019)选择性必修 第二册5.2 导数的运算优秀ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第二册5.2 导数的运算优秀ppt课件，共24页。PPT课件主要包含了学习目标，新课导入，复习回顾，导函数的概念，①求平均变化率，②取极限得导数，新知探究，归纳总结，典例解析，巩固练习等内容，欢迎下载使用。

能根据导数的定义推导常用函数的导数
掌握基本初等函数的导数公式
利用基本初等函数的导数公式解决有关问题，发展学生的数学运算素养
由导函数的定义可知，一个函数的导数是唯一确定的. 在必修第一册中我们学过基本初等函数，并且知道，很多复杂的函数都是通过对这些函数进行加、减、乘、除等运算得到的. 由此自然想到，能否先求出基本初等函数的导数，然后研究出导数的“运算法则”，这样就可以利用导数的运算法则和基本初等函数的导数求出复杂函数的导数. 本节我们就来研究这些问题.
下面我们根据定义来求一些常见函数的导数.
基本初等函数的导数公式的推导
问题1 前面我们学习了导数的定义，并且会用定义求函数在某一点处的导数，那么由导数定义求函数y=f (x)的导数的步骤是什么呢？
问题2 你能根据导数的定义，求出下列函数的导数吗？
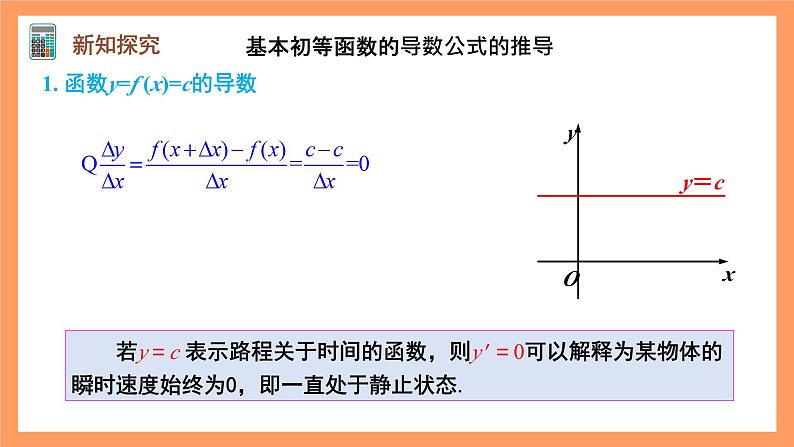
1. 函数y=f (x)=c的导数
若y＝c 表示路程关于时间的函数，则y′ ＝0可以解释为某物体的瞬时速度始终为0，即一直处于静止状态.
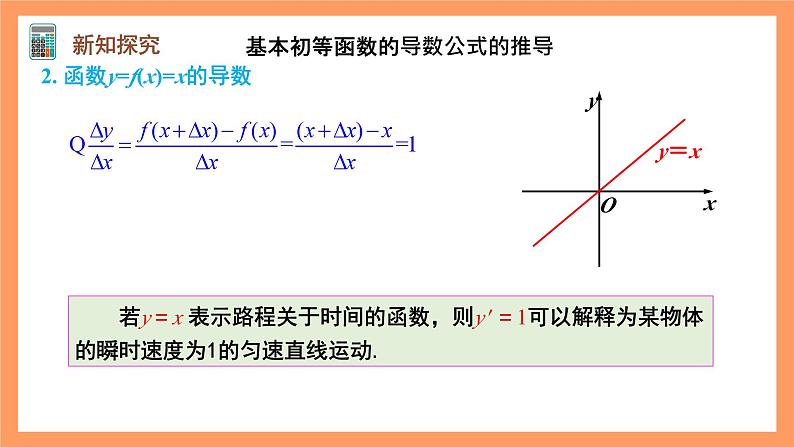
2. 函数y=f(x)=x的导数
若y＝x 表示路程关于时间的函数，则y′ ＝1可以解释为某物体的瞬时速度为1的匀速直线运动.
3. 函数y=f(x)=x2的导数
若y′＝2x表示函数y＝x2的图像上的点(x, y)处切线的斜率为2x ，说明随x的变化，切线的斜率也在变化，若y＝x2可表示路程关于时间的函数，则y′＝2x可以解释为某物体做变速运动，它在时刻x的瞬时速度为2x.
4. 函数y=f(x)=x3的导数
若y′＝3x2表示函数y＝x3的图像上的点(x, y)处切线的斜率为3x2,这说明随x的变化，切线的斜率也在变化，且恒为非负数.
探究 画出函数 的图象，根据图象，描述它的变化情况，并求出曲线在点(1, 1)处的切线方程.
函数y=f(x)=x的导数：y′ ＝1
函数y=f(x)=x2的导数：y′＝2x
函数y=f(x)=x3的导数：y′＝3x2
问题3 以上函数都是什么函数？它们的导函数有什么规律？
汇总以上公式，可以得到统一的公式：
请注意公式中的条件是 ,但根据我们所掌握的知识,只能就 的情况加以证明.这个公式称为幂函数的导数公式.事实上n可以是任意实数.
基本初等函数的导数公式
1. 求下列函数的导数:
2. 求下列函数在给定点处的导数:
例3 已知曲线y＝ln x，点P(e，1)是曲线上一点，求曲线在点P处的切线方程．
变式 求曲线y＝ln x的过点O(0，0)的切线方程．
利用导数的几何意义解决切线问题的两种情况(1)若已知点是切点，则在该点处的切线斜率就是该点处的导数．(2)如果已知点不是切点，则应先设出切点，再借助两点连线的斜率公式进行求解．