高中数学人教B版 (2019)选择性必修 第三册6.2.2 导数与函数的极值、最值课文课件ppt

这是一份高中数学人教B版 (2019)选择性必修 第三册6.2.2 导数与函数的极值、最值课文课件ppt，共35页。PPT课件主要包含了新知初探·自主学习，课堂探究·素养提升，fx≤fx0，y极大＝fx0，fx≥fx0，y极小＝fx0，极大值点与极小值点，答案B，答案C，答案D等内容，欢迎下载使用。

1.借助函数的图象，了解函数在某点取得极值的必要条件和充分条件；2．能利用导数求某些函数的极大值、极小值．
教 材 要 点知识点　极值点和极值的概念
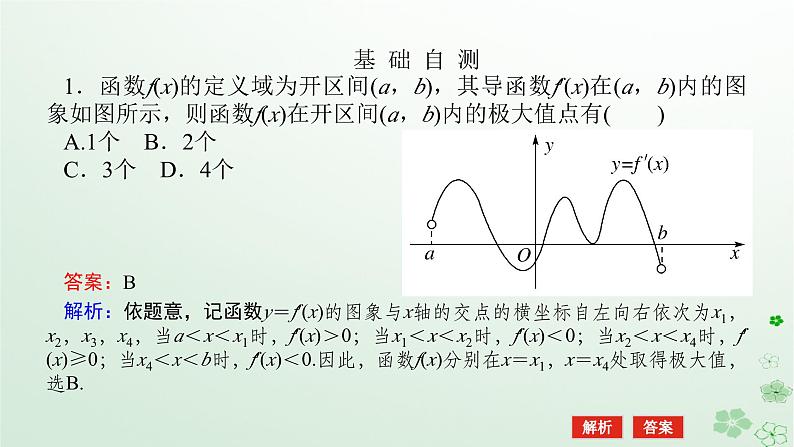
　基 础 自 测1．函数f(x)的定义域为开区间(a，b)，其导函数f′(x)在(a，b)内的图象如图所示，则函数f(x)在开区间(a，b)内的极大值点有(　　)A.1个 B．2个C．3个 D．4个
解析：依题意，记函数y＝f′(x)的图象与x轴的交点的横坐标自左向右依次为x1，x2，x3，x4，当a＜x＜x1时，f′(x)＞0；当x1＜x＜x2时，f′(x)＜0；当x2＜x＜x4时，f′(x)≥0；当x4＜x＜b时，f′(x)＜0.因此，函数f(x)分别在x＝x1，x＝x4处取得极大值，选B.
2．函数y＝x3－3x2－9x(－2＜x＜2)有(　　)A．极大值5，极小值－27B．极大值5，极小值－11C．极大值5，无极小值D．极小值－27，无极大值
解析：由y′＝3x2－6x－9＝0，得x＝－1或x＝3.当x＜－1或x＞3时，y′＞0；由－1＜x＜3时，y′＜0.∴当x＝－1时，函数有极大值5；3∉(－2，2)，故无极小值．
方法归纳1．解答此类问题要先搞清楚所给的图象是原函数还是导函数的，对于导函数的图象，重点考查在哪个区间上为正，哪个区间上为负，在哪个点处与x轴相交，在该点附近的导数值是如何变化的，若是由正值变为负值，则在该点处取得极大值；若是由负值变为正值，则在该点处取得极小值．
2．注意点：(1)极值点不是点；(2)极值是函数的局部性质；(3)函数的极值不唯一；(4)极大值与极小值两者的大小不确定；(5)极值点出现在区间的内部，端点不能是极值点；(6)若f′(x0)＝0，则x0不一定是极值点，即f′(x0)＝0是f(x)在x＝x0处取到极值的必要不充分条件，函数y＝f′(x)的变号零点，才是函数的极值点．
跟踪训练1　已知函数y＝f(x)的导函数y＝f′(x)的图象如图所示，则函数y＝f(x)在区间(a，b)内的极小值点的个数为(　　)A．1　　　B．2　　　C．3　　　D．4
解析：由图象，设f′(x)与x轴负半轴的两个交点的横坐标分别为c，d，其中c　求函数的极值例2　求下列函数的极值．(1)f(x)＝x2－2x－1；
【解析】f′(x)＝2x－2，令f′(x)＝0，解得x＝1.因为当x<1时，f′(x)<0，当x>1时，f′(x)>0，所以函数在x＝1处有极小值，且y极小＝－2.
【解析】f′(x)＝x3－2x2＋x＝x(x2－2x＋1)＝x(x－1)2.令f′(x)＝0，解得x1＝0，x2＝1.所以当x变化时，f′(x)，f(x)的变化情况如下表： 所以当x＝0时，函数取得极小值，且y极小＝－6.
(3)f(x)＝|x|；
【解析】显然函数f(x)＝|x|在x＝0处不可导，当x>0时，f′(x)＝x′＝1>0，函数f(x)＝|x|在(0，＋∞)内单调递增；当x<0时，f′(x)＝(－x)′＝－1<0，函数f(x)＝|x|在(－∞，0)内单调递减．故当x＝0时，函数取得极小值，且y极小＝0.
(4)f(x)＝x－a ln x(a∈R)．
方法归纳1．讨论函数的性质要注意定义域优先的原则．2．极值点与导数的关系(1)可导函数的极值点一定是导数值为0的点，导数值为0的点不一定是极值点．点x0是可导函数f(x)在区间(a，b)内的极值点的充要条件：①f′(x0)＝0；②点x0两侧f′(x)的符号不同．(2)不可导的点可能是极值点(如本例(3)中x＝0点)，也可能不是极值点(如y＝√(x)，在x＝0处不可导，在x＝0处也取不到极值)，所以函数的极值点可能是f′(x)＝0的根，也可能是不可导点．
跟踪训练2　求下列函数的极值：(1)f(x)＝x2－2ln x；
(2)f(x)＝x3－x；
(3)f(x)＝x2e－x.
状元随笔　求导得f ′(x)＝x2＋2(a－1)x＋1，再解不等式[2(a－1)]2－4≤0即得解． 
方法归纳已知函数极值的情况，逆向应用确定函数的解析式时，应注意以下两点：1．根据极值点处导数为0和极值两个条件列方程组，利用待定系数法求解；2．因为导数值等于零不是此点为极值点的充要条件，所以利用待定系数法求解后必须验证根的合理性．
跟踪训练3　(1)已知f(x)＝x3＋3ax2＋bx＋a2在x＝－1时有极值0，求常数a，b的值． 
解析：由题意知，f′(x)＝x2＋ax＋a，由函数f(x)有极小值和极大值，得方程f′(x)＝0有两个不同的实根，所以Δ＝a2－4a>0⇒a<0或a>4，即a的取值范围为(－∞，0)∪(4，＋∞).故选C.