人教版八年级上册第十二章 全等三角形12.1 全等三角形达标测试

这是一份人教版八年级上册第十二章 全等三角形12.1 全等三角形达标测试，文件包含人教版八年级数学上册第12章全等三角形测试卷原卷版docx、人教版八年级数学上册第12章全等三角形测试卷解析版docx、人教版八年级数学上册第12章全等三角形测试卷答题卡docx等3份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
1．（2020·河北省初二期末）如图，△ABE≌△ACF，若AB=5，AE=2，则EC的长度是（ ）
A．2B．3C．4D．5
【答案】B
【解析】
解：∵△ABE≌△ACF，AB＝5，AE＝2，
∴AB＝AC＝5，
∴EC=AC-AE=5-2=3，
故选：B．
2．（2020·陕西省初三二模）如图，在四边形中，对角线AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有（ ）
A．1对B．2对C．3对D．4对
【答案】C
【解析】∵AB=AD，CB=CD，AC公用，∴△ABC≌△ADC（SSS）．
∴BAO=DAO，BCO=DCO．
∴△BAO≌△DAO（SAS），△BCO≌△DCO（SAS）．
∴全等三角形共有3对．故选C．
3．（2020·福州四十中金山分校初二月考）如图，在△ABC和△DEF中，∠B＝∠DEF，AB＝DE，若添加下列一个条件后，仍然不能证明△ABC≌△DEF，则这个条件是( )
A．∠A＝∠DB．BC＝EFC．∠ACB＝∠FD．AC＝DF
【答案】D
【解析】解：∵∠B=∠DEF，AB=DE，∴添加∠A=∠D，利用ASA可得△ABC≌△DEF；
∴添加BC=EF，利用SAS可得△ABC≌△DEF；
∴添加∠ACB=∠F，利用AAS可得△ABC≌△DEF；
故选D．
4．（2022·河南省初二期中）如图，已知MB=ND，∠MBA=∠NDC，下列哪个条件不能判定△ABM≌△CDN（ ）
A．AM=CN B．AB=CD C．AM∥CN D．∠M=∠N
【答案】A
【解析】
解：A、MB=ND，AM=CN ，∠MBA=∠NDC，△ABM和△CDN不一定全等，错误，符合题意；
B、∵MB=ND，AM=CN ，AB=CD ，∴△ABM≌△CDN（SSS）， 正确，不符合题意；
C、∵ AM∥CN，∴∠A=∠NCD，又∠MBA=∠NDC，MB=ND，∴△ABM≌△CD（AAS）， 正确，不符合题意；
D、∵∠M=∠N，MB=ND，∠MBA=∠NDC，∴△ABM≌△CDN（ASA），正确，不符合题意；
故答案为：A.
5．（2022·湖北省初二期中）如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是
A．BC=EC，∠B=∠EB．BC=EC，AC=DC
C．BC=DC，∠A=∠DD．∠B=∠E，∠A=∠D
【答案】C
【解析】
A、已知AB=DE，加上条件BC=EC，∠B=∠E可利用SAS证明△ABC≌△DEC，故此选项不合题意；
B、已知AB=DE，加上条件BC=EC，AC=DC可利用SSS证明△ABC≌△DEC，故此选项不合题意；
C、已知AB=DE，加上条件BC=DC，∠A=∠D不能证明△ABC≌△DEC，故此选项符合题意；
D、已知AB=DE，加上条件∠B=∠E，∠A=∠D可利用ASA证明△ABC≌△DEC，故此选项不合题意．
故选C．
6．（2020·曲靖市沾益区播乐乡罗木中学初二月考）下列三角形不一定全等的是（ ）
A．有两个角和一条边对应相等的三角形
B．有两条边和一个角对应相等的三角形
C．斜边和一锐角对应相等的两个直角三角形
D．三条边对应相等的两个三角形
【答案】B
【解析】根据全等三角形的判定：ASA或AAS可知：有两个角和一条边对应相等的两个三角形全等，故A不正确；
当有两边和一角对应相等的两三角形，只有当两边及其夹角对应相等时，即SAS，两三角形全等，故B正确；
根据一锐角对应相等时，直角和另一锐角也对应相等，故根据ASA或AAS可判断两三角形全等，故C不正确；
根据三边对应相等的两三角形全等（SSS），故D不正确.
故选：B.
7．（2020·江西省初一月考）有一个小口瓶（如图所示），想知道它的内径是多少，但是尺子不能伸到里边直接测，于是拿两根长度相同的细木条，把两根细木条的中点固定在一起，木条可以绕中点转动，这样只要量出AB的长，就可以知道玻璃瓶的内径是多少，那么△OAB≌△OCD理由是（ ）
A．边角边B．角边角C．边边边D．角角边
【答案】A
【解析】 根据SAS得：△OAB≌△OCD.则AB=CD.
故选A.
8．（2020·哈尔滨工业大学附属中学校初一期中）如图，在△ABC和△CDE中，若∠ACB＝∠CED＝90°，AB＝CD，BC＝DE，则下列结论中不正确的是( )
A．△ABC≌△CDEB．CE＝ACC．AB⊥CDD．E为BC的中点
【答案】D
【解析】
在Rt△ABC和Rt△CDE中，
∴△ABC≌△CDE，
∴CE=AC，∠D=∠B，
∴CD⊥AB，
D：E为BC的中点无法证明
故A、B、C.正确，
故选. D
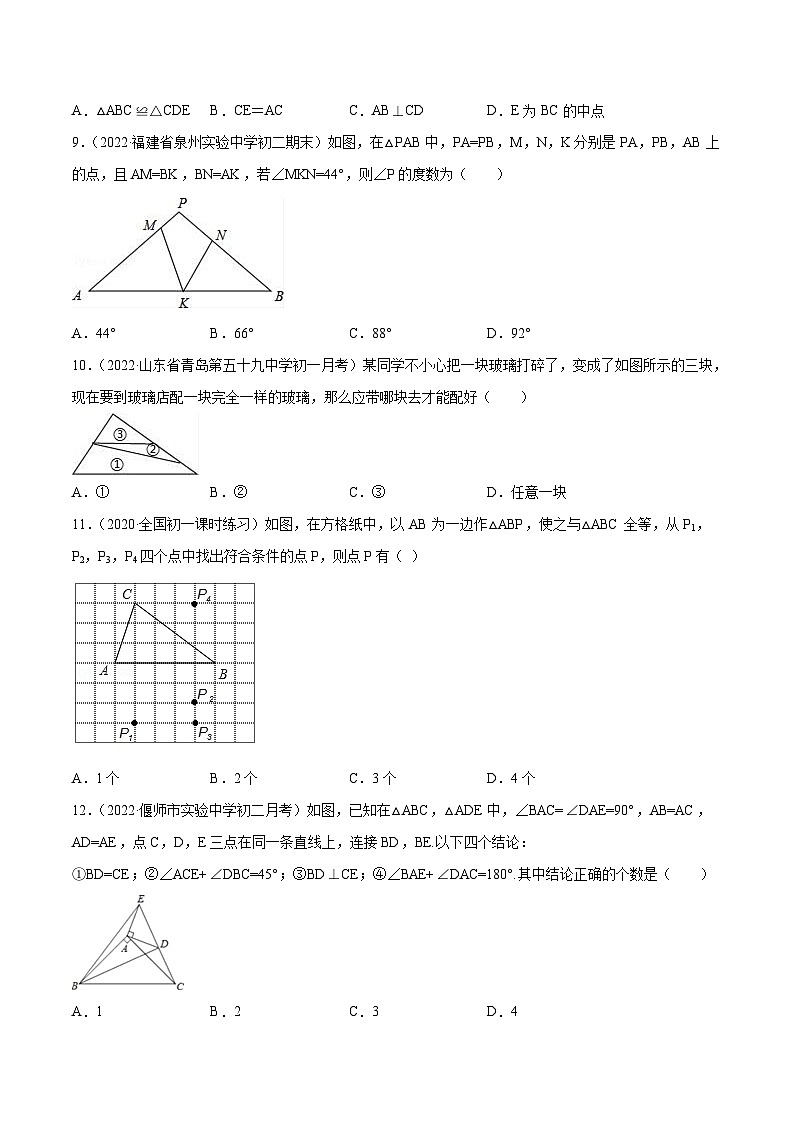
9．（2022·福建省泉州实验中学初二期末）如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（ ）
A．44°B．66°C．88°D．92°
【答案】D
【解析】
解：∵PA=PB，∴∠A=∠B，∵AM=BK，BN=AK，
∴

故选D.
10．（2022·山东省青岛第五十九中学初一月考）某同学不小心把一块玻璃打碎了，变成了如图所示的三块，现在要到玻璃店配一块完全一样的玻璃，那么应带哪块去才能配好（ ）
A．①B．②C．③D．任意一块
【答案】A
【解析】解：只第①块玻璃中包含两角及这两角的夹边，符合ASA．
故选A．
11．（2020·全国初一课时练习）如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（ ）
A．1个B．2个C．3个D．4个
【答案】C
【解析】
要使△ABP与△ABC全等，必须使点P到AB的距离等于点C到AB的距离，即3个单位长度，所以点P的位置可以是P1，P2，P4三个，故选C.
12．（2022·偃师市实验中学初二月考）如图，已知在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE.以下四个结论：
①BD=CE；②∠ACE+∠DBC=45°；③BD⊥CE；④∠BAE+∠DAC=180°.其中结论正确的个数是（ ）
A．1B．2C．3D．4
【答案】D
【解析】如图：①∵∠BAC=∠DAE=90°，
∴∠BAC+∠DAC=∠DAE+∠DAC，
即∠BAD=∠CAE．
在△ABD和△ACE中，
,
∴△ABD≌△ACE（SAS），
∴BD=CE，
∴①正确；
②∵∠BAC=90°，AB=AC，
∴∠ABC=45°，
∴∠ABD+∠DBC=45°．
∴∠ACE+∠DBC=45°，
∴②正确；
∵△ABD≌△ACE，
∴∠ABD=∠ACE．
∵∠CAB=90°，
∴∠ABD+∠AFB=90°，
∴∠ACE+∠AFB=90°．
∵∠DFC=∠AFB，
∴∠ACE+∠DFC=90°，
∴∠FDC=90°．
∴BD⊥CE，
∴③正确；
④∵∠BAC=∠DAE=90°，∠BAC+∠DAE+∠BAE＋∠DAC=360°,
∴∠BAE＋∠DAC=180°,故④正确.
所以①②③④都正确，共计4个.
故选D.
13．（2020·江西科技学院附属中学初二月考）中，厘米，，厘米，点D为AB的中点如果点P在线段BC上以v厘米秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动若点Q的运动速度为3厘米秒，则当与全等时，v的值为
A．B．3C．或3D．1或5
【答案】C
【解析】①当BD=PC时，
∵点D为AB的中点，
∴BD=AB=6厘米，
∵BD=PC，
∴BP=9-6=3（厘米），
∴CQ =BP=3厘米，
∴点Q运动了3÷3=1秒
∴点P在线段BC上的运动速度是3÷1=3（厘米秒），
②当BD=CQ时，
∴BD=CQ=6厘米，
点Q运动了6÷3=2秒.
∵△BDP≌△CQP，
∴BP=CP=厘米，
∴点P在线段BC上的运动速度是÷2=2.25（厘米秒），
故选C.
14．（2021·长沙市开福区青竹湖湘一外国语学校初二开学考试）如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按图中所标注的数据，计算图中实线所围成的面积S是（ ）
A．50B．62C．65D．68
【答案】A
【解析】
∵如图，AE⊥AB且AE=AB,EF⊥FH,BG⊥FH⇒∠EAB=∠EFA=∠BGA=90º，∠EAF+∠BAG=90º，∠ABG+∠BAG=90º⇒∠EAF=∠ABG，
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG⇒△EFA≌△AGB，
∴AF=BG，AG=EF.
同理证得△BGC≌△CHD得GC=DH，CH=BG.
故FH=FA+AG+GC+CH=3+6+4+3=16
故S= (6+4)×16−3×4−6×3=50.
故选A.
二、填空题（本题共4个小题；每个小题3分，共12分，把正确答案填在横线上）
15．（2020·宁津县育新中学初一期中）如图，两个大小一样的直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB＝10，DH＝4，平移距离为6，则阴影部分面积是_____
【答案】48
【解析】根据题意得：DE=AB=10；BE=CF=6；CH∥DF，
∴EH=10﹣4=6；EH：HD=EC：CF，即6：4=EC：6，
∴EC=9，∴S△EFD=×10×（9+6）=75；S△ECH=×9×6=27，
∴S阴影部分=75﹣27=48．故答案为48．
16．（2020·万杰朝阳学校初一期中）如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=_________
【答案】135°
【解析】
∵AC=BE，BC=DE，∠ACB=∠BED=90°，
∴△ABC≌△BDE（SAS），
∴∠1=∠DBE，
∵∠DBE+∠3=90°，
∴∠1+∠3=90°，
∵∠2=×90°=45°，
∴∠1+∠2+∠3=90°+45°=135°．
故答案是：135°．
17．（2017·河南省初二期中）如图，直线经过正方形的顶点分别过此正方形的顶点、作于点、 于点．若，则的长为________．
【答案】13
【解析】∵ABCD是正方形(已知)，
∴AB=AD,∠ABC=∠BAD=90°；
又∵∠FAB+∠FBA=∠FAB+∠EAD=90°，
∴∠FBA=∠EAD(等量代换)；
∵BF⊥a于点F，DE⊥a于点E，
∴在Rt△AFB和Rt△AED中，
∵，
∴△AFB≌△AED(AAS)，
∴AF=DE=8,BF=AE=5(全等三角形的对应边相等)，
∴EF=AF+AE=DE+BF=8+5=13.
故答案为13.
18．（2020·广西壮族自治区初三期末）如图，△ABC是不等边三角形，DE＝BC，以D，E为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以画出______个．
【答案】4
【解析】如图，能画4个,分别是:以D为圆心,AB为半径画圆;以C为圆心,CA为半径画圆．两圆相交于两点（DE上下各一个）,分别于D、E连接后,可得到两个三角形；以D为圆心,AC为半径画圆;以E为圆心,AB为半径画圆．两圆相交于两点（DE上下各一个）,分别于D、E连接后,可得到两个三角形．因此最多能画出4个
19．（2022·吉林省初二期末）如图，在平面直角坐标系中，已知点A(0，3)，B(9，0)，且∠ACB＝90°，CA＝CB，则点C的坐标为________．
【答案】(6，6)
【解析】如图,过点C作CE⊥OA，CF⊥OB，
∵∠AOB=，
∴四边形OECF是矩形，
∴∠ECF=，
∵∠ACB=，
∴∠ACE=∠BCE
在△ACE和△BCF中,
∴△ACE≌△BCF，
∴CE=CF，
∵四边形OECF是矩形，
∴矩形OECF是正方形，
∴OE=OF，
∵AE=OE−OA=OE−3，BF=OB−OF=9−OF，
∴OE=OF=6，
∴C(6,6)，
故答案为(6,6).
三、解答题（本题共8道题，19-21每题6分，22-25每题8分，26题10分，满分60分）
20．（2020·湖北省初三一模）如图，点E、F在BC上，BE＝CF，AB＝DC，∠B＝∠C．求证：∠A＝∠D．
【答案】答案见解析
【解析】解∵BE＝CF，
∴BE+EF＝CF+EF，即BF＝CE．
在△ABF和△DCE中，

∴△ABF≌△DCE，
∴∠A＝∠D．
21．（2022·广西壮族自治区初三学业考试）已知：如图，∠BAC=∠DAM，AB=AN，AD=AM，求证：∠B=∠ANM．
【答案】证明见解析.
【解析】证明：∵∠BAC=∠DAM，∠BAC=∠BAD+∠DAC，∠DAM=∠DAC+∠NAM，
∴∠BAD=∠NAM．
在△BAD和△NAM中，∵AB=AN，∠BAD=∠NAM，AD=AM，
∴△BAD≌△NAM（SAS），
∴∠B=∠ANM．
22．（2020·河南省初二期末）如图，在△ABC中，∠BAC=50°，∠C=60°，AD⊥BC，
（1）用尺规作图作∠ABC的平分线BE，且交AC于点E，交AD于点F（不写作法，保留作图痕迹）；
（2）求∠BFD的度数．
【答案】（1）见解析；（2）55°
【解析】解：（1）如图所示，BE即为所求；
（2）∵∠BAC＝50°，∠C＝60°，
∴∠ABC＝180°−∠BAC−∠C＝70°，
由（1）知BE平分∠ABC，
∴∠DBC＝∠ABC＝35°，
又∵AD⊥BC，
∴∠ADB＝90°，
则∠BFD＝90°−∠DBC＝55°．
23．（2020·衡水市第九中学初二期中）已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE
【答案】详见解析
【解析】证明：如图，过点C作CF⊥AD交AD的延长线于F，
∵AC平分∠BAD，CE⊥AB，
∴CE＝CF，
∵∠B＋∠ADC＝180°．
∠ADC＋∠CDF＝180°（平角定义），
∴∠CDF＝∠B，
在△CDF和△CBE中，
，
∴△CDF≌△CBE（AAS），
∴DF＝BE，
在Rt△ACF和Rt△ACE中，
，
∴Rt△ACF≌Rt△ACE（HL），
∴AE＝AF，
∵AF＝AD＋DF，
∴AE＝AD＋BE．
24．（2020·偃师市实验中学初二月考）如图，AD⊥BC于D，AD=BD，AC=BE．
（1）请说明∠1=∠C；
（2）猜想并说明DE和DC有何特殊关系．
【答案】见解析
【解析】
（1）∵AD⊥BC于D，∴∠BDE=∠ADC=90°．
∵AD=BD，AC=BE，∴Rt△BDE≌Rt△ADC（HL），∴∠1=∠C．
（2）DE=DC．理由如下：
由（1）知△BDE≌△ADC，∴DE=DC．
25．（2020·山东省初三一模）如图甲，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作等腰直角三角形ADE，AD=AE，∠DAE=90º.解答下列问题：
(1) 如果AB=AC，∠BAC=90º．
①当点D在线段BC上时（与点B不重合），如图乙，线段CE、BD之间的位置关系为，数量关系为．（不用证明）
②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？

(2) 如果AB≠AC，∠BAC≠90º，点D在线段BC上运动．
试探究：当△ABC满足一个什么条件时，CE⊥BD（点C、E重合除外）？画出相应的图形，并说明理由．
【答案】见解析
【解析】解：（1）①CE与BD位置关系是CE⊥BD，数量关系是CE=BD.
理由：如图乙,
∵∠BAD=90°−∠DAC,∠CAE=90°−∠DAC，
∴∠BAD=∠CAE.
又BA=CA，AD=AE，
∴△ABD≌△ACE(SAS)
∴∠ACE=∠B=45°且CE=BD.
∵∠ACB=∠B=45°，
∴∠ECB=45°+45°=90°，即CE⊥BD.
故答案为：CE⊥BD；CE=BD.
②当点D在BC的延长线上时,①的结论仍成立.
如图丙,
∵∠DAE=90°,∠BAC=90°，
∴∠DAE=∠BAC，
∴∠DAB=∠EAC，
又AB=AC，AD=AE，
∴△DAB≌△EAC，
∴CE=BD，且∠ACE=∠ABD.
∵∠BAC=90°，AB=AC，
∴∠ABC=45°，
∴∠ACE=45°，
∴∠BCE=∠ACB+∠ACE=90°，
即 CE⊥BD；
（2）如图丁所示,当∠BCA=45°时,CE⊥BD.
理由：过点A作AG⊥AC交BC于点G，
∴AC=AG,∠AGC=45°，
即△ACG是等腰直角三角形，
∵∠GAD+∠DAC=90°=∠CAE+∠DAC，
∴∠GAD=∠CAE，
又∵DA=EA，
∴△GAD≌△CAE，
∴∠ACE=∠AGD=45°，
∴∠BCE=∠ACB+∠ACE=90°，
即CE⊥BD.
26．（2020·福州四十中金山分校初二月考）（问题提出）
学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
（初步思考）
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
（深入探究）
第一种情况：当∠B是直角时，△ABC≌△DEF．
（1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据 ，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是钝角时，△ABC≌△DEF．
（2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．
第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
（3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）
（4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若 ，则△ABC≌△DEF．
【答案】（1）HL；（2）证明见解析；（3）作图见解析；（4）∠B≥∠A．
【解析】（1）解：HL；
（2）证明：如图，过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H，
∵∠B=∠E，且∠B、∠E都是钝角，
∴180°-∠B=180°-∠E，
即∠CBG=∠FEH，
在△CBG和△FEH中，
∴△CBG≌△FEH（AAS），
∴CG=FH，
在Rt△ACG和Rt△DFH中，
AC=DF，CG=FH
∴Rt△ACG≌Rt△DFH（HL），
∴∠A=∠D，
在△ABC和△DEF中，
∴△ABC≌△DEF（AAS）；
（3）解：如图，△DEF和△ABC不全等；
（4）解：若∠B≥∠A，则△ABC≌△DEF．