



- 专题06 图形与坐标(重难点,浙江期末精选)-2023-2024学年八年级数学上学期期中期末高分突破(浙教版) 试卷 2 次下载
- 专题07 一次函数(重点,浙江期末精选)-2023-2024学年八年级数学上学期期中期末高分突破(浙教版) 试卷 1 次下载
- 特训01 三角形的初步认识压轴题(浙江精品归纳)-2023-2024学年八年级数学上学期期中期末高分突破(浙教版) 试卷 1 次下载
- 特训02 三角形的初步认识压轴题(新题速递)-2023-2024学年八年级数学上学期期中期末高分突破(浙教版) 试卷 1 次下载
- 特训03 全等三角形压轴题(八大题型归纳)-2023-2024学年八年级数学上学期期中期末高分突破(浙教版) 试卷 3 次下载
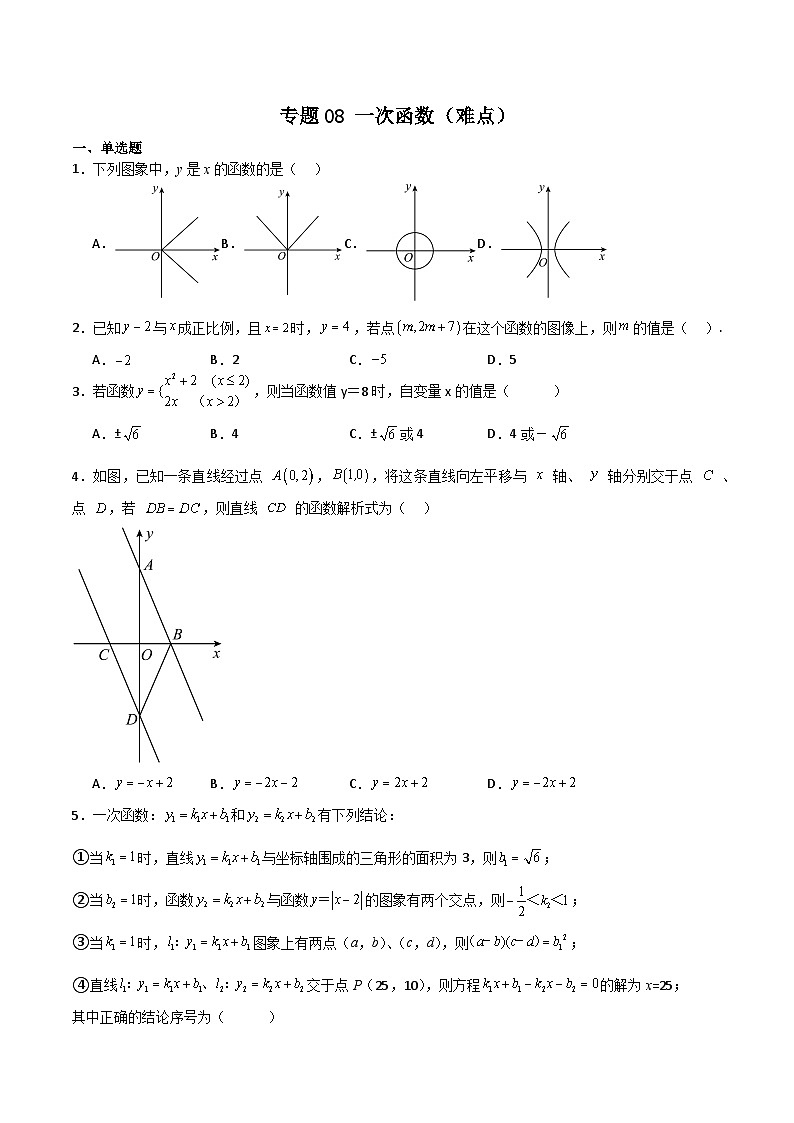
专题08 一次函数(难点)-2023-2024学年八年级数学上学期期中期末高分突破(浙教版)
展开1.下列图象中,y是x的函数的是( )
A.B.C.D.
2.已知与成正比例,且时,,若点在这个函数的图像上,则的值是( ).
A.B.2C.D.5
3.若函数,则当函数值y=8时,自变量x的值是( )
A.±B.4C.±或4D.4或-
4.如图,已知一条直线经过点 ,,将这条直线向左平移与 轴、 轴分别交于点 、点 ,若 ,则直线 的函数解析式为( )
A.B.C.D.
5.一次函数:和有下列结论:
①当时,直线与坐标轴围成的三角形的面积为3,则;
②当时,函数与函数的图象有两个交点,则;
③当时,图象上有两点(a,b)、(c,d),则;
④直线交于点P(25,10),则方程的解为x=25;
其中正确的结论序号为( )
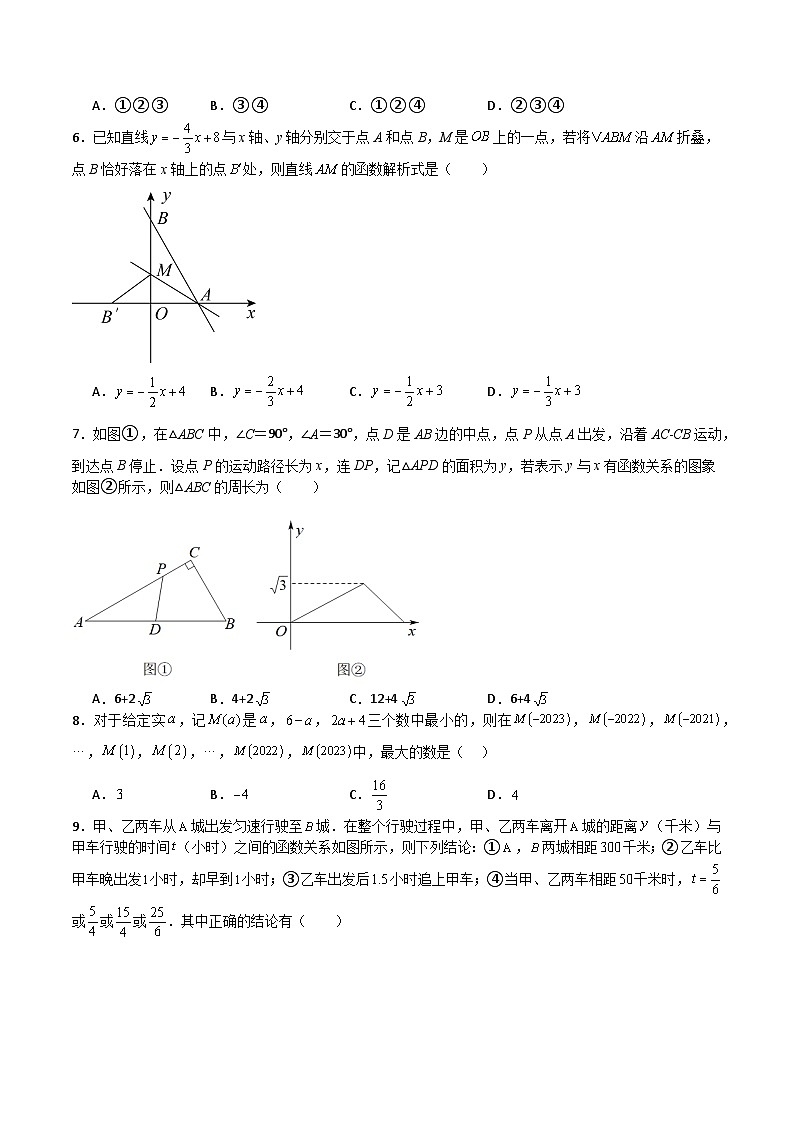
A.①②③B.③④C.①②④D.②③④
6.已知直线与x轴、y轴分别交于点A和点B,M是上的一点,若将沿折叠,点B恰好落在x轴上的点处,则直线的函数解析式是( )
A.B.C.D.
7.如图①,在△ABC中,∠C=90°,∠A=30°,点D是AB边的中点,点P从点A出发,沿着AC﹣CB运动,到达点B停止.设点P的运动路径长为x,连DP,记△APD的面积为y,若表示y与x有函数关系的图象如图②所示,则△ABC的周长为( )
A.6+2B.4+2C.12+4D.6+4
8.对于给定实,记是,,三个数中最小的,则在,,,,,,,,中,最大的数是( )
A.B.C.D.
9.甲、乙两车从城出发匀速行驶至城.在整个行驶过程中,甲、乙两车离开城的距离(千米)与甲车行驶的时间(小时)之间的函数关系如图所示,则下列结论:①,两城相距千米;②乙车比甲车晚出发小时,却早到小时;③乙车出发后小时追上甲车;④当甲、乙两车相距千米时,或或或.其中正确的结论有( )
A.个B.个C.个D.个
10.如图,在平面直角坐标系中,点A的坐标为(4,0),点Q是直线yx上的一个动点,以AQ为边,在AQ的右侧作等边△APQ,使得点P落在第一象限,连接OP,则OP+AP的最小值为( )
A.6B.4C.8D.6
二、填空题
11.已知y与z成正比例函数,且当时,,z与x成一次函数关系,函数关系式为,且过点,则y是x的 函数,函数关系式为 .
12.无论 m 取任何实数,一次函数必过一定点,此定点坐标为 ;线段 AB 的端点分别为 A(1,3),B(3,0),一次函数图像与线段 AB 相交,则m 的取值范围是 .
13.不论m取什么实数,点A(m+1,m2+2m-5)都在某函数图像上,若B(a,b)也是该函数图像上的点,则a2-b= .
14.已知一次函数,原点到直线的最大距离为 .
15.若,满足,且为常数),则称点为“和谐点”.一次函数存在“和谐点”,则b的取值范围 .
16.小颖和小明骑自行车从滨江路上相距米的A、两地同时出发,相向而行,行驶一段时间后小颖的自行车坏了,立刻停车并马上打电话通知小明,小明接到电话后立刻提速至原来的倍,碰到小颖后用了分钟修好了小颖的自行车,修好车后小明立刻骑车以提速后的速度继续向终点A地前行,小颖则留在原地整理工具,分钟以后小颖以原速向走了分钟后,发现小明的包在自己身上,马上掉头以原速的倍的速度返回A地,在整个行驶过程中,小颖和小明均保持匀速行驶小明停车和打电话的时间忽略不计,两人相距的路程米与小颖出发的时间分钟之间的关系如图所示,则小明到达A地时,小颖与A地的距离为 米.
17.如图,直线:与坐标轴交于、两点,点为第一象限内一点,连接且轴,交直线于点,连接,,将沿着直线翻折,得到,点正好落在直线上,若,那么点C的坐标为 .
18.如图,已知,点P在线段上(点P不与点A重合),点Q在线段上,,当最小时,点Q的坐标 .
三、解答题
19.在平面直角坐标系中,直线l:y=kx+1(k≠0)与直线x=k,直线y=﹣k分别交于点A,B,直线x=k与直线y=﹣k交于点C.
(1)求直线l与y轴的交点坐标;
(2)横、纵坐标都是整数的点叫作整点.记线段AB,BC,CA围成的区域(不含边界)为W.
①当k=2时,结合函数图象,求区域W内的整点个数;
②若区域W内没有整点,直接写出k的取值范围.
20.阅读下列一段话:材料1:已知平面直角坐标系内两点、,则这两点的距离可以用下列公式计算:,例如点、,则这两点的距离.材料2在平在直角坐标系中,以任意两点、为端点的线段中点坐标为,例如已知点,,则线段PQ的中点M的坐标为,即,解答下列问题:如图,已知点A(2,4)、B(6,2),线段AB的中点为C
(1)求线段AB的长度和中点C的坐标;
(2)若点M为轴上的一个动点,当MA=MB时,求点M的坐标及直线MC的解析式.
21.已知函数y=,其中m为常数,该函数图象记为G.
(1)当m=1时.
①若点A(a,4)在图象G上,求a的值.
②当﹣1≤x≤2时,直接写出函数值y的取值范围.
(2)点B在图象G上,点B的横坐标为2m.
①用含m的代数式表示点B的坐标.
②当m>0时,直线y=4m与图象G交于点C、D,当△BCD的面积为9时,求点B的坐标.
③过点B作x轴的垂线,与直线y=x+交于点H,当BH≥2时,直接写出m的取值范围.
22.如图,在平面直角坐标系中,为等腰直角三角形,,,点A的坐标为.
(1)求点B的坐标;
(2)在x轴上存在一点P,使得的和最小,求出这个最小值;
(3)在第四象限是否存在一点M,使得以点O,A,M为顶点的三角形是等腰直角三角形,若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
23.如图:在平面直角坐标系中,直线与x,y轴分别交于点A,点B,已知点.
(1)求出点A,B的坐标;
(2)点P是直线上的一个动点,且,求点P的坐标;
(3)如图2,过点C作y轴的平行线m,在直线m上是否存在点Q,使得是等腰直角三角形?若存在请直接写出符合条件的Q点坐标,若不存在,请说明理由.
24.甲、乙两家蓝莓采摘园的蓝莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案.甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠.优惠期间,设某游客的蓝莓采摘量为x (千克),在甲采摘园所需总费用为(元),在乙采摘园所需总费用为(元).根据题意列出下表:
(1)变化过程中采摘量x(千克)和在甲采摘园所需总费用(元),这两个变量中,自变量是_____,因变量是_____,表格中m的值为_____;
(2)当蓝莓采摘量超过10千克时,求表示在乙采摘园所需总费用和采摘量x这两个变量之间关系的表达式;
(3)如图,是小刚画出的表示在甲采摘园所需总费用(元)和在乙采摘园所需总费用(元)分别与采摘量x(千克)之间关系的图象.
①图中两图象的交点A表示的意义是:______________________________;
②若要采摘50千克蓝莓,去哪家比较合算?结合图象,你认为小刚应选择去哪家蓝莓采摘园采摘比较合算.
25.如图,在平面直角坐标系中,直线:与x轴交于点,与y轴交于点B,直线:与x轴交于点C,与y轴交于点D,两直线交于点.
(1)求直线的表达式;
(2)点P是直线上的一个动点,若,求点P的坐标;
(3)点M是y轴正半轴上的一点,且,Q在直线上的一个动点,连接与 过点E的x轴的垂线l交于点N,连接,当平分时,请直接写出点Q的坐标.
26.如图,在平面直角坐标系中,点O为坐标原点,点,点B在x轴负半轴上,,.
(1)求B点坐标;
(2)如图1,动点C从点B出发,以每秒个单位长度的速度沿x轴正方向运动,运动时间为t秒,的面积为S,请用用含有t的式子表示S;(不要求写出t的取值范围)
(3)如图2,在(2)的条件下,当时,点C停止运动此时的角平分线交于点D,交y轴于点E、在x轴上有一点P,平面内有一点,连接.若,求的面积.
采摘量:x(千克)
5
10
15
20
…
在甲采摘园所需总费用:(元)
150
240
330
m
…
在乙采摘园所需总费用:(元)
150
300
375
450
…
专题08 简单事件的概率重难点题型专训(八大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版): 这是一份专题08 简单事件的概率重难点题型专训(八大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版),文件包含专题08简单事件的概率重难点题型专训八大题型原卷版docx、专题08简单事件的概率重难点题型专训八大题型解析版docx等2份试卷配套教学资源,其中试卷共63页, 欢迎下载使用。
特训08 一元一次不等式 压轴题-2023-2024学年八年级数学上学期期中期末高分突破(浙教版): 这是一份特训08 一元一次不等式 压轴题-2023-2024学年八年级数学上学期期中期末高分突破(浙教版),文件包含特训08一元一次不等式压轴题原卷版docx、特训08一元一次不等式压轴题解析版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
专题07 一次函数(重点,浙江期末精选)-2023-2024学年八年级数学上学期期中期末高分突破(浙教版): 这是一份专题07 一次函数(重点,浙江期末精选)-2023-2024学年八年级数学上学期期中期末高分突破(浙教版),文件包含专题07一次函数重点浙江期末精选原卷版docx、专题07一次函数重点浙江期末精选解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。












