八年级数学上学期期中测试卷02（苏科版）（原卷版+解析版）-【学霸满分】2023-2024学年八年级数学上册重难点专题提优训练（苏科版）

这是一份八年级数学上学期期中测试卷02（苏科版）（原卷版+解析版）-【学霸满分】2023-2024学年八年级数学上册重难点专题提优训练（苏科版），文件包含八年级数学上学期期中测试卷02苏科版原卷版docx、八年级数学上学期期中测试卷02苏科版解析版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

注意事项：
1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。
3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。
4．测试范围：第一-第三单元（苏科版）。
5．考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷
单项选择题（本题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
1．在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）
A．B．C．D．
【答案】A
【解答】解：A、是轴对称图形，故本选项正确；
B、不是轴对称图形，故本选项错误；
C、不是轴对称图形，故本选项错误；
D、不是轴对称图形，故本选项错误．
故选：A．
2．下列计算正确的是（ ）
A．B．＝3C．D．＝
【答案】B
【解答】解：A、+无法计算，故此选项错误；
B、+＝+2＝3，正确；
C、+＝﹣2+，故此选项错误；
D、﹣＝2﹣2，故此选项错误；
故选：B．
3．如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）
A．带①去B．带②去C．带③去D．带①和②去
【答案】C
【解答】解：A、带①去，仅保留了原三角形的一个角和部分边，不能得到与原来一样的三角形，故A选项错误；
B、带②去，仅保留了原三角形的一部分边，也是不能得到与原来一样的三角形，故B选项错误；
C、带③去，不但保留了原三角形的两个角还保留了其中一条边，符合ASA判定，故C选项正确；
D、带①和②去，仅保留了原三角形的一个角和部分边，同样不能得到与原来一样的三角形，故D选项错误．
故选：C．
4．如图，直线a、b、c表示三条互相交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）
A．1处B．2处C．3处D．4处
【答案】D
【解答】解：∵△ABC内角平分线的交点到三角形三边的距离相等，
∴△ABC内角平分线的交点满足条件；
如图：点P是△ABC两条外角平分线的交点，
过点P作PE⊥AB于E，PD⊥BC于D，PF⊥AC于F，
∴PE＝PF，PF＝PD，
∴PE＝PF＝PD，
∴点P到△ABC的三边的距离相等，
∴△ABC两条外角平分线的交点到其三边的距离也相等，满足这条件的点有3个；
综上，到三条公路的距离相等的点有4个，
∴可供选择的地址有4个．
故选：D．
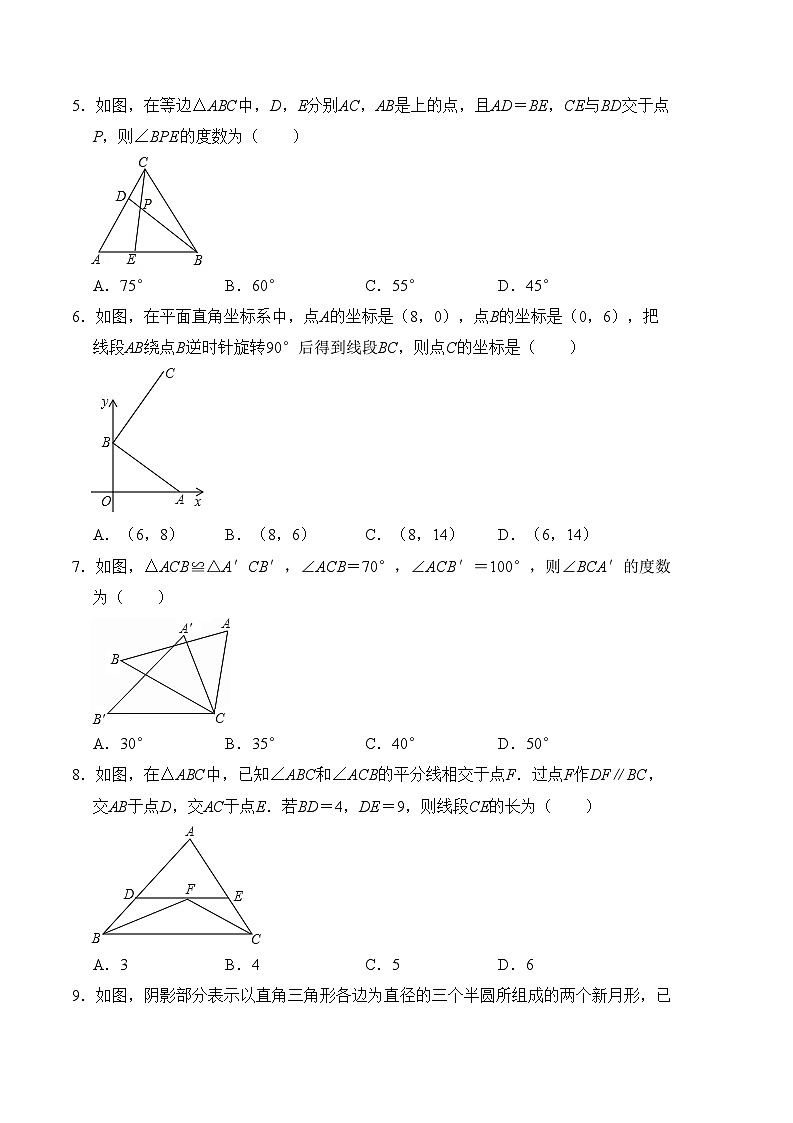
5．如图，在等边△ABC中，D，E分别AC，AB是上的点，且AD＝BE，CE与BD交于点P，则∠BPE的度数为（ ）
A．75°B．60°C．55°D．45°
【答案】B
【解答】解：∵△ABC是等边三角形，
∴AC＝BC，∠A＝∠CBE＝60°，
又知BD＝CE，
在△ABD和△CBE中，
，
∴△ABD≌△BCE（SAS），
∴∠DBA＝∠BCE，
∵∠BPE＝∠BCE+∠CBP，
∴∠BPE＝∠ABD+∠CBP＝∠ABC＝60°，
故选：B．
6．如图，在平面直角坐标系中，点A的坐标是（8，0），点B的坐标是（0，6），把线段AB绕点B逆时针旋转90°后得到线段BC，则点C的坐标是（ ）
A．（6，8）B．（8，6）C．（8，14）D．（6，14）
【答案】D
【解答】解：作CH⊥y轴于H．
∵A（8，0），B（0，6），
∴OA＝8，OB＝6，
∵∠AOB＝∠ABC＝∠CHB＝90°，
∴∠CBH+∠ABO＝90°，∠ABO+∠BAO＝90°，
∴∠CBH＝∠BAO，
∵BC＝BA，
∴△CHB≌△BOA（AAS），
∴BH＝OA＝8，CH＝OB＝6，
∴OH＝8+6＝14，
∴C（6，14），
故选：D．
7．如图，△ACB≌△A′CB′，∠ACB＝70°，∠ACB′＝100°，则∠BCA′的度数为（ ）
A．30°B．35°C．40°D．50°
【答案】C
【解答】解：∵△ACB≌△A′CB′，
∴∠A′CB′＝∠ACB＝70°，
∵∠ACB′＝100°，
∴∠BCB′＝∠ACB′﹣∠ACB＝30°，
∴∠BCA′＝∠A′CB′﹣∠BCB′＝40°，
故选：C．
8．如图，在△ABC中，已知∠ABC和∠ACB的平分线相交于点F．过点F作DF∥BC，交AB于点D，交AC于点E．若BD＝4，DE＝9，则线段CE的长为（ ）
A．3B．4C．5D．6
【答案】C
【解答】解：∵∠ABC和∠ACB的平分线相交于点F，
∴∠DBF＝∠FBC，∠ECF＝∠BCF，
∵DF∥BC，交AB于点D，交AC于点E．
∴∠DFB＝∠DBF，∠CFE＝∠BCF，
∴BD＝DF＝4，FE＝CE，
∴CE＝DE﹣DF＝9﹣4＝5．
故选：C．
9．如图，阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形，已知S1+S2＝7，且AC+BC＝8，则AB的长为（ ）
A．6B．2C．5D．
【答案】A
【解答】解：由勾股定理得，AC2+BC2＝AB2，
∵S1+S2＝7，
∴×π×（）2+×π×（）2+×AC×BC﹣×π×（）2＝7，
∴AC×BC＝14，
AB＝＝＝6，
故选：A．
10．如图，A，B两点在正方形网格的格点上，每个方格都是边长为1的正方形，点C也在格点上，且△ABC为等腰三角形，满足条件的点C有（ ）
A．6个B．7个C．8个D．9个
【答案】D
【解答】解：①点C以点A为标准，AB为底边，符合点C的有5个；
②点C以点B为标准，AB为等腰三角形的一条边，符合点C的有4个．
所以符合条件的点C共有9个．
故选：D．
第Ⅱ卷
填空题（本题共6小题，每小题2分，共12分．）
11．16的算术平方根是 4 ．
【答案】见试题解答内容
【解答】解：∵42＝16，
∴＝4．
故答案为：4．
12．平面直角坐标系中，点A（2，3）关于x轴的对称的点的坐标是 （2，﹣3） ．
【答案】见试题解答内容
【解答】解：点A（2，3）关于x轴的对称点的坐标是（2，﹣3），
故答案为：（2，﹣3）．
13．如图，长方形ABCD的边AB落在数轴上，A、B两点在数轴上对应的数分别为﹣1和1，BC＝1，连接BD，以B为圆心，BD为半径画弧交数轴于点E，则点E在数轴上所表示的数为 1﹣ ．
【答案】1﹣．
【解答】解：在Rt△ABD中，
AB＝1﹣（﹣1）＝2，AD＝BC＝1，
∴BD＝＝＝，
∵以B为圆心，BD为半径画弧交数轴于点E，
∴BE＝BD＝，
∴E点表示的数为1﹣，
故答案为：1﹣．
14．如图，要为一段高5米，长13米的楼梯铺上红地毯，至少需要红地毯 17 米．
【答案】见试题解答内容
【解答】解：根据勾股定理，楼梯水平长度为＝12米，
则红地毯至少要12+5＝17米长，
故答案为：17．
15．矩形ABCD中，AB＝10，BC＝3，E为AB边的中点，P为CD边上的点，且△AEP是腰长为5的等腰三角形，则DP＝ 4或1或9 ．
【答案】见试题解答内容
【解答】解：（1）如图1，当AE＝EP＝5时，
过P作PM⊥AB，
∴∠PMB＝90°，
∵四边形ABCD是矩形，
∴∠B＝∠C＝90°，
∴四边形BCPM是矩形，
∴PM＝BC＝3，
∵PE＝5，
∴EM＝＝＝4，
∵E是AB中点，
∴BE＝5，
∴BM＝PC＝5﹣4＝1，
∴DP＝10﹣1＝9；
（2）如图2，当AE＝AP＝5时，DP＝＝＝4；
（3）如图3，当AE＝EP＝5时，
过P作PF⊥AB，
∵四边形ABCD是矩形，
∴∠D＝∠DAB＝90°，
∴四边形BCPF是矩形，
∴PF＝AD＝3，
∵PE＝5，
∴EF＝＝4，
∵E是AB中点，
∴AE＝5，
∴DP＝AF＝5﹣4＝1．
故答案为：1或4或9．
16．如图，在边长为2的等边△ABC中，D是BC的中点，点E在线段AD上，连接BE，在BE的下方作等边△BEF，连接DF．当△BDF的周长最小时，∠DBF的度数是 30° ．
【答案】见试题解答内容
【解答】解：如图，连接CF，
∵△ABC、△BEF都是等边三角形，
∴AB＝BC＝AC，BE＝EF＝BF，∠BAC＝∠ABC＝∠ACB＝∠EBF＝∠BEF＝∠BFE＝60°，
∴∠ABC﹣∠EBD＝∠EBF﹣∠EBD，
∴∠ABE＝∠CBF，
在△BAE和△BCF中，
，
∴△BAE≌△BCF（SAS），
∴∠BCF＝∠BAD＝30°，
如图，作点D关于CF的对称点G，连接CG，DG，则FD＝FG，
∴当B，F，G在同一直线上时，DF+BF的最小值等于线段BG长，且BG⊥CG时，△BDF的周长最小，
由轴对称的性质，可得∠DCG＝2∠BCF＝60°，CD＝CG，
∴△DCG是等边三角形，
∴DG＝DC＝DB，
∴∠DBG＝∠DGB＝∠CDG＝30°，
故答案为：30°．
三、解答题（本题共7小题，共54分．解答应写出文字说明、证明过程或演算步骤．）
17．（6分）计算：
（1）； （2）．
【答案】（1）8；
（2）2+．
【解答】解：（1）原式＝3+5+
＝8；
（2）原式＝2﹣+2
＝2+．
（6分）求x的值：
（1）4x2＝81； （2）2（x﹣1）3＝54．
【答案】见试题解答内容
【解答】解：（1）4x2＝81
x2＝，
解得：x＝±；
（2）（x﹣1）3＝27，
x﹣1＝3，
解得：x＝4．
19．（8分）如图，△ABC中，AD是BC边上的中线，E，F为直线AD上的点，连接BE，CF，且BE∥CF．
（1）求证：△BDE≌△CDF；
（2）若AE＝13，AF＝7，试求DE的长．
【答案】（1）证明见解答；
（2）DE＝3．
【解答】（1）证明：∵AD是BC边上的中线，
∴BD＝CD，
∵BE∥CF，
∴∠DBE＝∠DCF，
在△BDE和△CDF中，
，
∴△BDE≌△CDF（ASA）；
（2）解：∵AE＝13，AF＝7，
∴EF＝AE﹣AF＝13﹣7＝6，
∵△BDE≌△CDF，
∴DE＝DF，
∵DE+DF＝EF＝6，
∴DE＝3
20．（6分）（1）已知2a﹣1的平方根是±3，3a+b﹣1的平方根是±4，求a+2b的平方根；
（2）若x，y都是实数，且y＝+8，求x+3y的立方根．
【答案】（1）±3．
（2）3．
【解答】解：（1）由题意可知：2a﹣1＝9，3a+b﹣1＝16，
∴a＝5，b＝2，
∴a+2b＝5+4＝9，
∴9的平方根是±3，即a+2b的平方根为±3．
（2）由题意可知：，
∴x＝3，
∴y＝8，
∴x+3y＝3+24＝27，
∴27的立方根是3，即x+3y的立方根是3
21．（8分）如图1，∠AOB＝90°，OC平分∠AOB，以C为顶点作∠DCE＝90°，交OA于点D，OB于点E．
（1）求证：CD＝CE；
（2）图1中，若OC＝3，求OD+OE的长；
（3）如图2，∠AOB＝120°，OC平分∠AOB，以C为顶点作∠DCE＝60°，交OA于点D，OB于点E．若OC＝3，求四边形OECD的面积．
【答案】见试题解答内容
【解答】（1）证明：如图1，过点C作CG⊥OA于G，CH⊥OB于H，
∵OC平分∠AOB，
∴CG＝CH
∵∠AOB＝90°，∠DCE＝90°，
∴∠CDO+∠CEO＝180°，
∵∠CDG+∠CDO＝180°，
∴∠CDG＝∠CEO，
在△CDG与△CEH中
，
∴△CDG≌△CEH（AAS），
∴CD＝CE；
（2）解：由（1）得△CDG≌△CEH，
∴DG＝HE，
由题易得△OCG与△OCH是全等的等腰直角三角形，且OG＝OH，
∴OD+OE＝OD+OH+HE＝OG+OH＝2OH，
设OH＝CH＝x，在Rt△OCH中，由勾股定理，得：
OH2+CH2＝OC2
∴x2+x2＝32
∴（舍负）
∴OH＝
∴OD+OE＝2OH＝；
（3）解：如图，过点C作CG⊥OA于G，CH⊥OB于H，
∵OC平分∠AOB，
∴CG＝CH，
∵∠A0B＝120°，∠DCE＝60°，
∴∠CDO+∠CEO＝180°，
∵∠CDG+∠CDO＝180°，
∴∠CDG＝∠CEO，
在△CDG与△CEH中
，
∴△CDG≌△CEH（AAS），
∴DG＝HE，
由题易得△OCG与△OCH是全等的直角三角形，且OG＝OH，
∴OD+OE＝OD+OH+HE＝OG+OH＝2OH，
∴S四边形OECD＝S四边形OHCG＝2S△OCG
在Rt△OCH中，有∠COH＝60°，OC＝3，
∴OH＝，CH＝
∴，
∴S四边形OECD＝2S△OCG＝．
22．（10分）如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形AOB，点C为x轴正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边三角形CBD，连接DA并延长，交y轴于点E．
（1）求证：OC＝AD；
（2）在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数；如果改变，请说明理由；
（3）当点C运动到什么位置时，以A、E、C为顶点的三角形是等腰三角形？
【答案】见试题解答内容
【解答】解：（1）∵△AOB，△CBD都是等边三角形，
∴OB＝AB，CB＝DB，∠ABO＝∠DBC，
∴∠OBC＝∠ABD，
在△OBC和△ABD中，
∵，
∴△OBC≌△ABD（SAS），
∴OC＝AD；
（2）点C在运动过程中，∠CAD的度数不会发生变化，理由如下：
∵△AOB是等边三角形，
∴∠BOA＝∠OAB＝60°，
∵△OBC≌△ABD，
∴∠BAD＝∠BOC＝60°，
∴∠CAD＝180°﹣∠OAB﹣∠BAD＝60°；
（3）∵△OBC≌△ABD，
∴∠BOC＝∠BAD＝60°，
又∵∠OAB＝60°，
∴∠OAE＝180°﹣60°﹣60°＝60°，
∴∠EAC＝120°，∠OEA＝30°，
∴以A，E，C为顶点的三角形是等腰三角形时，AE和AC是腰，
在Rt△AOE中，OA＝1，∠OEA＝30°，
∴AE＝2，
∴AC＝AE＝2，
∴OC＝1+2＝3，
∴当点C的坐标为（3，0）时，以A，E，C为顶点的三角形是等腰三角形．
23．（10分）已知点A（a，0），B（0，b），a与b满足﹣12b+36＝0．点C为AB的中点．
（1）如图1，求AC的长；
（2）如图2，E、F分别为OA上的动点，且∠ECF＝45°，求证：EF2＝OE2+AF2；
（3）如图3，点D在y轴正半轴上运动，以AD为腰向下作等腰Rt△ADM，∠DAM＝90°，T为线段OA的中点，连DT并延长至点N，使DT＝TN，连MN，求MN的最小值．
【答案】（1）3；
（2）证明见解析；
（3）3．
【解答】（1）解：∵﹣12b+36＝0，
∴＝0，
∴a＝﹣6，b＝6，
∴OA＝OB＝6，
∵∠AOB＝90°，
∴AB＝6，
∵C为AB的中点，
∴AC＝AB＝3；
（2）证明：如图2，连接OC，
由（1）知OA＝OB，∠CAO＝45°，
∵C为AB的中点，
∴OC＝CA，
∴∠COE＝∠CAF＝45°，
∵∠ECF＝45°，
∴∠ACF+∠OCE＝90°﹣∠ECF＝45°，
将△OCE绕点C逆时针旋转90°可得△ACH，点O与点A重合，点E的对应点为H．
则CH＝CE，∠COE＝∠CAH．
∴∠HAF＝∠CAF+∠CAH＝∠CAF+∠COE＝90°，
∴AF2+AH2＝HF2，
即OE2+AF2＝HF2，
∵∠HCF＝∠HCA+∠ACF＝∠OCE+∠ACF＝45°＝∠ECF，
在△CHF和△CEF中，
，
∴△CHF≌△CEF（SAS），
∴HF＝EF，
在Rt△HAF中，HF2＝AH2+AF2，
∴EF2＝OE2+AF2；
（3）解：如图3，连接AN．
∵AT＝OT，∠ATN＝∠OTD，DT＝NT，
∴△ATN≌△OTD（SAS），
∴∠NAT＝∠DOT＝90°，AN＝OD，
设D（0，t）（t＞0），则OD＝t，AN＝OD＝t，
∵∠DAM＝90°，∠NAT＝90°，
∴∠NAM+∠MAO＝∠OAD+∠MAO，
∴∠NAM＝∠OAD，
过M作ME⊥AN，交AN的延长线于E，
∵AM＝AD，∠MEA＝∠DOA，
∴△MEA≌△DOA（AAS），
∴AE＝OA＝6，ME＝OD＝t，
∴NE＝AE﹣AN＝6﹣t，
∴MN＝＝，
∴t＝3时，MN有最小值3．