初中数学4 一元一次不等式说课ppt课件

这是一份初中数学4 一元一次不等式说课ppt课件，共18页。PPT课件主要包含了教学目标，重难点，复习旧知导入新课，实际问题，典型例题，归纳新知，巩固练习提高能力，课堂小结，一元一次不等式的应用，课后作业等内容，欢迎下载使用。

1.进一步掌握一元一次不等式的解法
2.利用一元一次不等式解决简单的实际问题
1.掌握不等式的实际应用问题
2.挖掘题中的不等关系
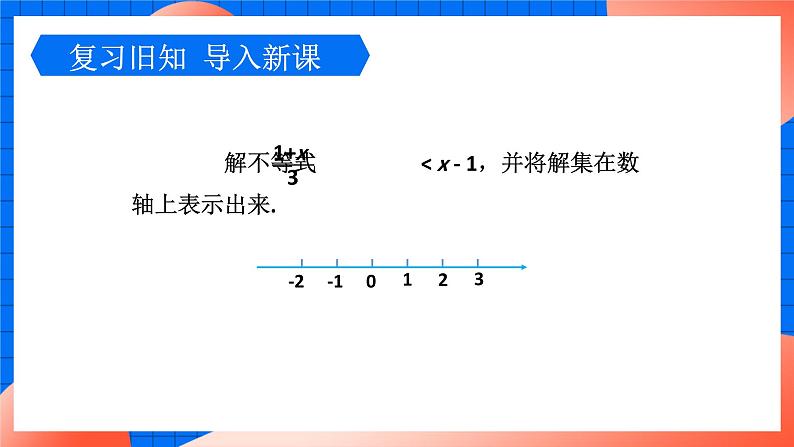
解：去分母，得 1 + x < 3x - 3.移项、合并同类项，得 -2x < -4.系数化为1，得x > 2.解集在数轴上表示如图所示.
解一元一次不等式的步骤：（1）去分母；（2）去括号；（3）移项；（4）合并同类项；（5）系数化为1.
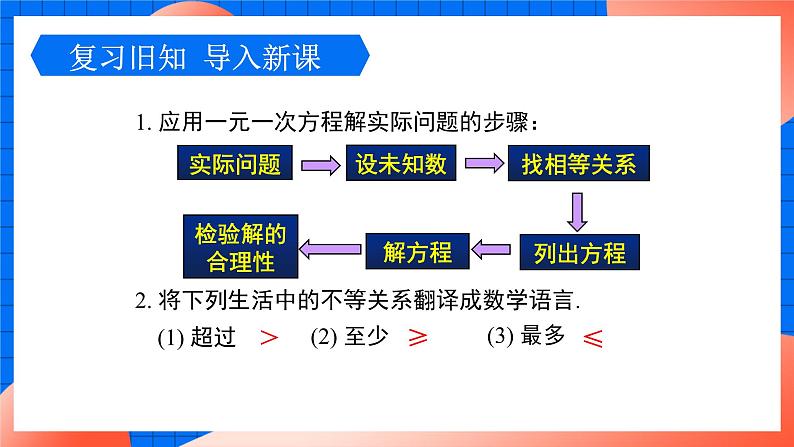
1. 应用一元一次方程解实际问题的步骤：
2. 将下列生活中的不等关系翻译成数学语言.
例1.一次环保知识竞赛共有25道题，规定答对一道题得4分，答错或不答一道题扣1分.在这次竞赛中，小明被评为优秀（85分或85分以上），小明至少答对了几道题？
解：设小明答对了x道题，则他答错和不答的共有（25-x）道题，根据题意，得：4x-1×(25-x)≥85.解这个不等式，得x≥22.所以，小明至少答对了22道题，他可能答对了22，23，24，25道题.
例2.小颖准备用21元钱买笔和笔记本.已知每支笔3元，每个笔记本2.2元，她买了2个笔记本.请你帮她算一算，她还可以买几支笔？
解：设她还可以买n支笔，根据题意得3n +2.2×2 ≤ 21，解这个不等式，得n ≤ .因为在这一问题中n只能取正整数，所以，小颖还可以买1支， 2支， 3支， 4支或5支笔.
你能总结出用一元一次不等式解决实际问题的一般步骤吗？
（1）审：认真审题找出不等关系；
（2）设：设出适当未知数；（3）列：根据题中的不等关系，列出不等式；（4）解：解所列的不等式；（5）答：根据实际情况写出答案.
1：小华打算在星期天与同学去登山，计划上午 7 点出发，到达山顶后休息 2 h，下午 4 点以前必须回到出发点. 如果他们去时的平均速度是 3 km/h，回来时的平均速度是 4 km/h，他们最远能登上哪座山顶 (图中数字表示出发点到山顶的路程)？
前面问题中涉及的数量关系是：
去时所花时间＋休息时间＋回来所花时间 ≤ 总时间.
他们在山顶休息了 2 h，又上午 7 点到下午 4 点之间总共相隔 9 h，即所用时间应小于或等于 9 h.
解得 x ≤ 12.
因此要满足下午 4 点以前必须返回出发点，小华他们最远能登上 D 山顶.
2.某市的一种出租车起步价为7元，起步路程为3 km(即开始行驶路程在3 km以内都需付7元)，超过3 km，每增加1km加价2.4元(不足1 km以1 km计价)，现在某人乘出租车从甲地到乙地，支付车费14.2元，问从甲地到乙地的路程最多是多少?
解：设从甲到乙地的路程为x 公里，则由题意，可得 7 + 2.4 (x - 3) ≤ 14.2 , 解得 x ≤6 . 所以 从甲地到乙地的路程最多是6 km.
3.某种商品的进价为400元，出售时标价为500元，商店准备打折出售，但要保持利润率不低于10%，则至多可打几折？
解：设至多可打x折，根据题意得≥ 10%，解这个不等式，得x ≥0.88. 则至多可打八八折.
总结解不等式的一般步骤、理论依据及注意事项.解一元一次不等式的一般步骤：（1）去分母———不等式的基本性质2或3.注意： ①勿漏乘不含分母的项； ②分子是两项或两项以上的代数式时要加括号； ③两边同时乘一个负数，须注意不等号的方向要改变.
（2）去括号———去括号法则和分配律.注意： ①勿漏乘括号内每一项； ②括号前面是“-”号，括号内各项要变号.（3）移项———移项法则（不等式的基本性质1）.注意：移项要变号.（4）合并同类项———合并同类项法则.（5）系数化为1 ———不等式的基本性质2或3.注意：两边同时除以未知数的系数时，要分清不等号的方向是否改变.
完成教材第49页习题2.5.