北师大版数学八年级下册 2.4.1《一元一次不等式》第1课时 课件+分层练习（含答案解析）

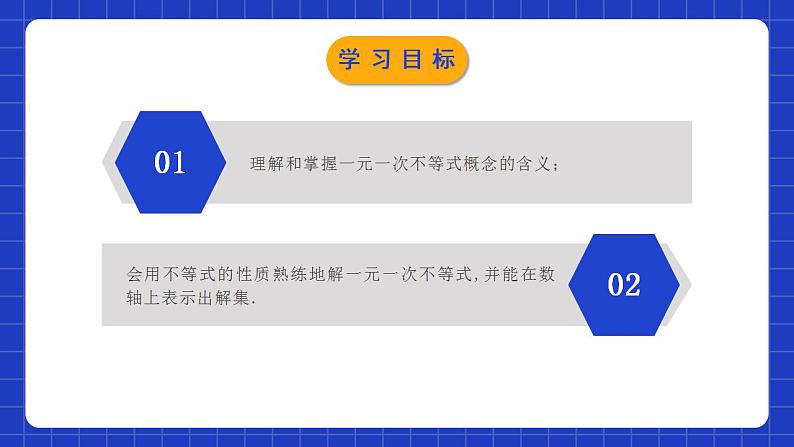
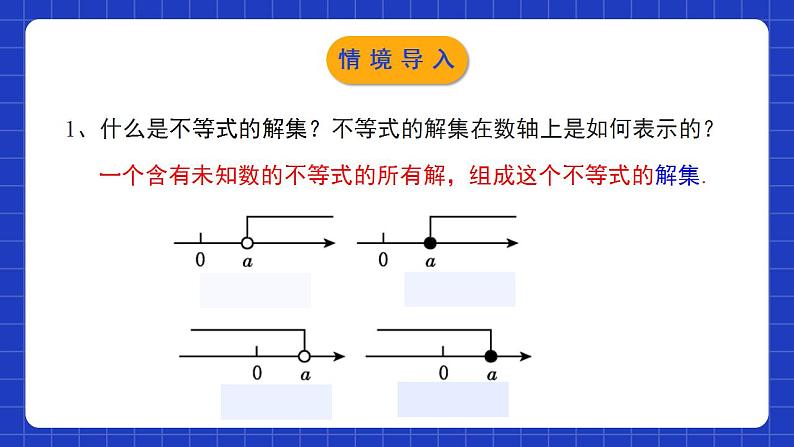
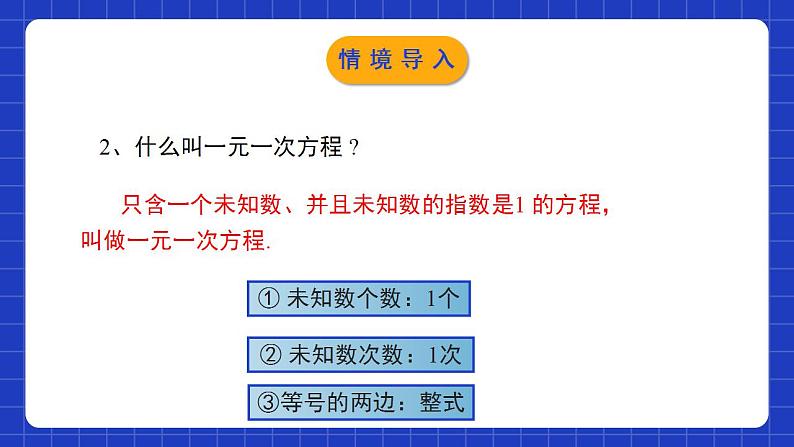
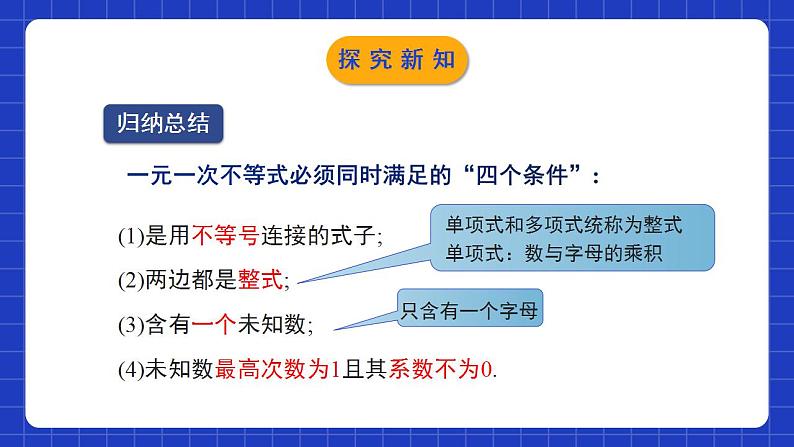
2.4.1一元一次不等式（第1课时）学习目标理解和掌握一元一次不等式概念的含义；0102会用不等式的性质熟练地解一元一次不等式,并能在数轴上表示出解集．一个含有未知数的不等式的所有解，组成这个不等式的解集.1、什么是不等式的解集？不等式的解集在数轴上是如何表示的？情境导入2、什么叫一元一次方程 ? 只含一个未知数、并且未知数的指数是1 的方程，叫做一元一次方程.① 未知数个数：1个② 未知数次数：1次③等号的两边：整式情境导入一元一次不等式的概念一元一次方程 只含有一个未知数，并且未知数的最高次数是1，且两边都为整式的等式叫做一元一次方程这些式子是什么？有什么特点？探究新知>≤<≥一元一次不等式 不等式的左右两边都是整式，只含有一个未知数，并且未知数的最高次数是1，像这样的不等式，叫做一元一次不等式.探究新知(1)是用不等号连接的式子;(2)两边都是整式;(3)含有一个未知数;(4)未知数最高次数为1且其系数不为0.一元一次不等式必须同时满足的“四个条件”:归纳总结探究新知练一练：下列不等式哪些是一元一次不等式？x-2＞3x+5 ( ) x≥0 ( )3-x＜2x+6 ( )x2+2x+1≥0 ( )( ) ( ) 是否是是是否探究新知解一元一次不等式例1：解不等式3-x<2x+6，并把它的解集表示在数轴上.怎样解一元一次不等式？解一元一次不等式和解一元一次方程一样吗？解一元一次方程，要根据等式的性质，将方程逐步化为x=a的形式；而解一元一次不等式，则要根据不等式的性质，将不等式逐步化为xa的形式.探究新知例1：解不等式3-x<2x+6，并把它的解集表示在数轴上.解：两边都加-2x，得 3-x-2x＜2x + 6-2x.合并同类项，得 3-3x＜6.两边都加-3, 得 3-3x-3＜6-3.合并同类项，得 -3x＜3两边都除以-3, 得 x＞-1x＞-1这个不等式的解集在数轴上的表示如图所示：探究新知讨论：对比一元一次方程的解法，你能总结出一元一次不等式的解题步骤吗？一元一次不等式的解法与一元一次方程的解法类似，其步骤：去分母去括号移项合并同类项系数化为1系数化为1时要注意什么？探究新知在运用性质3将系数化为1时要特别注意：不等式两边都乘以或除以同一个负数时，要改变不等号的方向.在数轴上表示解集应注意的问题：方向、空心或实心.归纳总结探究新知解：去分母，得3（x -2） ≥2（7-x） .去括号，得3x- 6≥14-2x .移项、合并同类项，得5x ≥20 .两边都除以5，得x≥4.这个不等式的解集在数轴上的表示如图所示：去分母要注意每一项都要乘最小公倍数,不要漏乘不含分母的项探究新知归纳总结解一元一次不等式的四点注意(1)去分母：去分母时要注意每一项都要乘以分母的最小公倍数.不要漏乘不含分母的项.(2)去括号：根据乘法的分配律不要漏乘项.(3)移项：移项要注意改变该项的符号,不等号方向不变.(4)系数化为1：两边都除以负数时注意不等号方向要改变.探究新知解一元一次方程的基本步骤：（1）去分母;（2）去括号;（3）移项、合并同类项;（4）化未知数系数为1;解一元一次不等式的基本步骤：（1）去分母;（2）去括号;（3）移项、合并同类项;（4）化未知数系数为1;（5）在数轴上表示不等式解集.归纳总结探究新知A随堂练习2.不等式2x-3>-5的解集在数轴上表示正确的是 (　 　)C随堂练习3. 不等式2(1-x)-4<0的解集是_______. x>-1　C随堂练习5、若(m+1)x|m|+2>0是关于x的一元一次不等式,则m=______. 　1　6、已知 (m+4)x|m|-3+6>0是关于x的一元一次不等式,则m的值为(　 　)　　　　　　　　　　　　　　　　　　A.4 B.±4 C.3 D.±3A随堂练习7.解下列不等式，并把它们的解集分别表示在数轴上：(1) x－4≥2(x＋2)； (2)解：(1) 去括号，得x－4≥2x＋4， 移项、合并同类项，得－x≥8，两边都除以－1，得x≤－8.这个不等式的解集在数轴上的表示如图所示．随堂练习7.解下列不等式，并把它们的解集分别表示在数轴上：(1) x－4≥2(x＋2)； (2)解：(2)去分母，得3(x－1)<2(4x－5)，去括号，得3x－3<8x－10，移项、合并同类项，得－5x<－7，两边都除以－5，得x>这个不等式的解集在数轴上的表示如图所示．随堂练习8、求不等式 的非负整数解解：去分母得：5(2x+1)≤3(3x-2)+15，去括号得：10x+5≤9x-6+15，移项得：10x-9x≤-5-6+15，合并同类项得x≤4，∴不等式的非负整数解为0、1、2、3、4．随堂练习 9. y取何正整数时，代数式2(y + 1)的值不大于3 - 4(y - 5)的值.解：根据题意列出不等式： 2(y + 1) ≤ 3 - 4(y – 5)去括号，可得 2y+2 ≤ 3 - 4y + 20移项，可得 2y+ 4y ≤ 3 + 20 - 2合并同类型，可得 6y ≤ 21解这个不等式，得y ≤ 3.5，不等式y ≤ 4的正整数解是：1，2，3.随堂练习1.一元一次不等式的判别条件：(1)都是整式；(2)只含一个未知数； (3)未知数的最高次数是1；(4)未知是数的系数不为0.2. 解一元一次不等式的一般步骤： (1)去分母；（注意符号）(2)去括号；(3)移项；(4)合并同类项；(5)未知数的系数化为1.（注意符号）课堂小结课程结束