初中数学人教版八年级下册17.2 勾股定理的逆定理备课ppt课件

这是一份初中数学人教版八年级下册17.2 勾股定理的逆定理备课ppt课件，文件包含第2课时勾股定理的逆定理的应用pptx、中国航海日mp4等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。

命题1 如果直角三角形两直角边长分别为 a，b，斜边长为 c，那么 a2+b2 = c2．
命题2 如果三角形 ABC 的三边长 a，b，c 满足 a2 + b2 = c2，那么这个三角形是直角三角形．
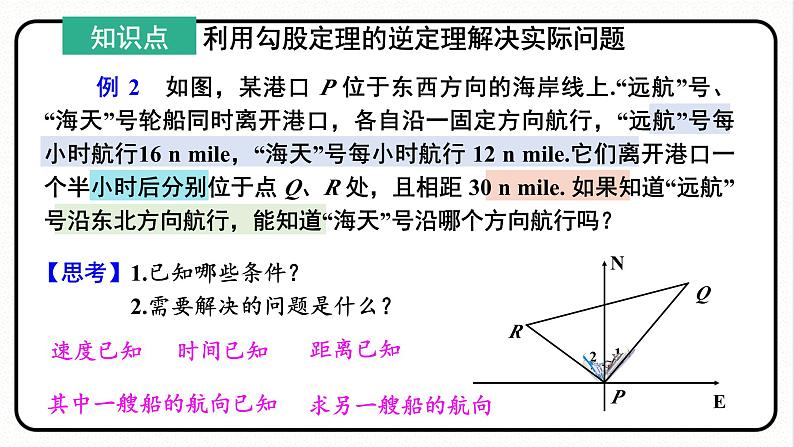
例 2　如图，某港口 P 位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16 n mile，“海天”号每小时航行 12 n mile.它们离开港口一个半小时后分别位于点 Q、R 处，且相距 30 n mile. 如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？
【思考】1.已知哪些条件？ 2.需要解决的问题是什么？
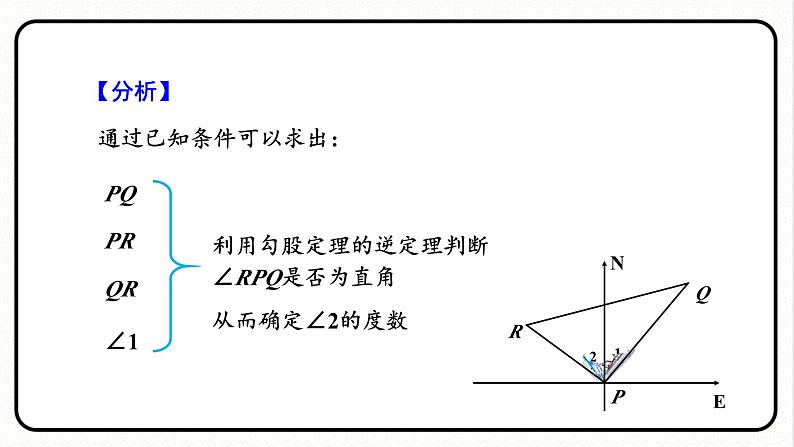
通过已知条件可以求出：
利用勾股定理的逆定理判断∠RPQ是否为直角
解：根据题意，PQ = 16×1.5 = 24，PR = 12×1.5 = 18，QR = 30.因为 242 + 182 = 302，即PQ2 + PR2 = QR2，所以∠QPR = 90°.∠1 = 45°.因此∠2 = 45°，即“海天”号沿西北方向航行.
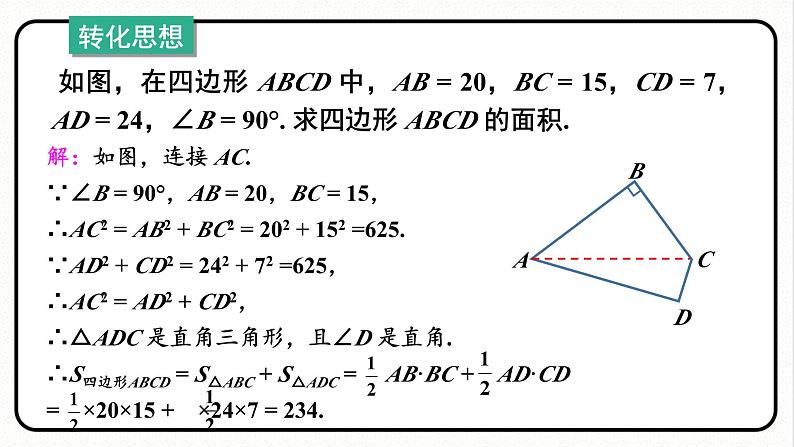
如图，在四边形 ABCD 中，AB = 20，BC = 15，CD = 7，AD = 24，∠B = 90°. 求四边形 ABCD 的面积.
1. 如果三条线段长 a，b，c 满足 a2 = c2-b2，这三条线段 组成的三角形是不是直角三角形？为什么？
解: 这三条线段组成的三角形是直角三角形.∵ a2 = c2-b2，∴ a2 + b2 = c2，由勾股定理的逆定理知这个三角形是直角三角形.
2. 说出下列命题的逆命题. 这些逆命题成立吗？ （1）两条直线平行，内错角相等； （2）如果两个实数相等，那么它们的绝对值相等；
其逆命题为“内错角相等，两直线平行”；这个命题成立.
其逆命题为“如果两个实数的绝对值相等，那么这两个实数相等”；这个命题不成立.如 |-3| = |3|，但 -3 ≠ 3.
（3）全等三角形的对应角相等； （4）在角的内部，到角的两边距离相等的点在角的平 分线上.
其逆命题为“对应角相等的两个三角形全等”；这个命题不成立.
其逆命题为“角平分线上的点到角两边的距离相等”；这个命题成立.
3. A，B，C 三地的两两距离如图所示，A 地在 B 地 的正东方向，C 地在 B 地的什么方向？
解：由图知：△ABC 中，AB = 12，BC = 5，AC = 13.∵ AB2 + BC2 = 122 + 52 = 144 + 25 = 169，∴AB2 + BC2 = AC2，由勾股定理的逆定理得△ABC 为直角三角形，且∠B = 90°.∵A 地在 B 地的正东方向，∴C 地在 B 地的正北方向.
1. 判断由线段 a，b，c 组成的三角形是不是直角三角形： （1）a = 7，b = 24，c = 25；
∵ a2 + b2 = 72 + 242 = 49 + 576 = 625，c2 = 252 = 625，∴ a2 + b2 = c2.由勾股定理的逆定理知这个三角形是直角三角形.
（2）a = ，b = 4，c = 5；
（3）a = ，b = 1，c = ；
（4）a = 40，b = 50，c = 60；
∵ a2 + b2 = 402 + 502 = 1600 + 2500 = 4100，c2 = 602 = 3600，∴ a2 + b2 ≠ c2.∴这个三角形不是直角三角形.
2.下列各命题都成立，写出它们的逆命题. 这些逆命题成立吗？ （1）同旁内角互补，两直线平行；
其逆命题为“两直线平行，同旁内角互补”；这个命题成立.
（2）如果两个角是直角，那么它们相等；
其逆命题为“如果两个角相等，那么它们都是直角”；这个命题不成立.
（3）全等三角形的对应边相等；
其逆命题为“如果两个三角形的三组边对应相等，那么这两个三角形全等”；这个命题成立.
（4）如果两个实数相等，那么它们的平方相等.
其逆命题为“如果两个实数的平方相等，那么这两个实数相等”；这个命题不成立.
3. 小明向东走 80 m 后， 沿另一方向又走了 60 m，再沿第三个方向走 100 m 回到原地. 小明向东走 80 m 后是向哪个方向走的？
解：小明的行走路线恰好构成三角形.∵ 602 + 802 = 3600 + 6400 = 10000 = 1002，∴ 这个三角形是直角三角形.∵小明向东走 80 m，∴小明又向北或南走 60 m.
4. 在△ABC 中，AB =13，BC = 10，BC 边上的中线 AD =12. 求 AC.
5. 如图，在四边形 ABCD 中，AB = 3，BC = 4，CD = 12， AD = 13，∠B = 90°. 求四边形 ABCD 的面积.
6. 如图，在正方形 ABCD 中，E 是 BC 的中点，F 是 CD 上一点，且 CF = CD. 求证∠AEF = 90°.
证明：设 CF = x，则 EC = BE = 2x，DF = 3x，AD = AB = 4x. 由勾股定理得：EF2 = EC2 + FC2 = 5x2，AE2 = AB2 + BE2 = 20x2，AF2 = AD2 + DF2 = 25x2 = 25x2，∴EF2 + AE2 = 25x2 = AF2.由勾股定理的逆定理知，∠AEF = 90°.
7. 我们知道 3，4，5 是一组勾股数，那么 3k，4k，5k（k 是正整数）也是一组勾股数吗？一般地，如果 a，b， c 是一组勾股数，那么 ak，bk，ck（k 是正整数）也是 一组勾股数吗？
解：3k，4k，5k 也是一组勾股数.∵ (3k)2 + (4k)2 = 9k2 + 16k2 = 25k2，(5k)2 = 25k2，∴(3k)2 + (4k)2 = (5k)2.如果a，b，c是一组勾股数，那么ak，bk，ck也是一组勾股数.∵a，b，c 是勾股数，则 a2 + b2 = c2，(ak)2 + (bk)2 = a2k2 + b2k2 = (a2 + b2)k2 = c2k2，(ck)2 = c2k2，故(ak)2 + (bk)2 = (ck)2，∴ak，bk，ck 也是一组勾股数.