人教版数学7年级下册 第六单元 复习题6 教案2
展开数学七年级上总复习
之实数
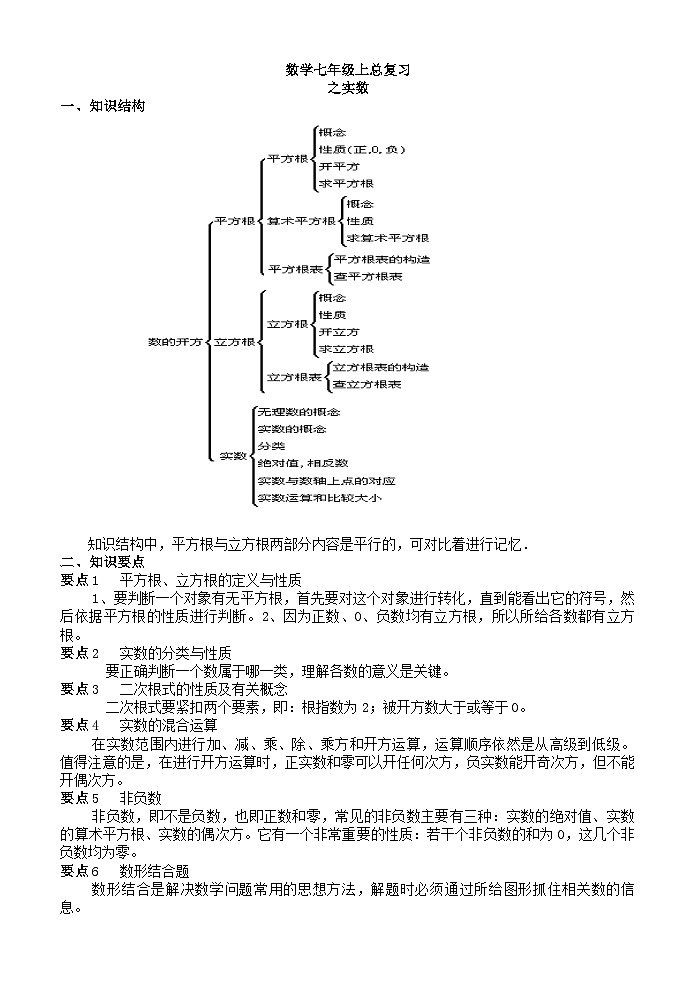
一、知识结构
知识结构中,平方根与立方根两部分内容是平行的,可对比着进行记忆.
二、知识要点
要点1 平方根、立方根的定义与性质
1、要判断一个对象有无平方根,首先要对这个对象进行转化,直到能看出它的符号,然后依据平方根的性质进行判断。2、因为正数、0、负数均有立方根,所以所给各数都有立方根。
要点2 实数的分类与性质
要正确判断一个数属于哪一类,理解各数的意义是关键。
要点3 二次根式的性质及有关概念
二次根式要紧扣两个要素,即:根指数为2;被开方数大于或等于0。
要点4 实数的混合运算
在实数范围内进行加、减、乘、除、乘方和开方运算,运算顺序依然是从高级到低级。值得注意的是,在进行开方运算时,正实数和零可以开任何次方,负实数能开奇次方,但不能开偶次方。
要点5 非负数
非负数,即不是负数,也即正数和零,常见的非负数主要有三种:实数的绝对值、实数的算术平方根、实数的偶次方。它有一个非常重要的性质:若干个非负数的和为0,这几个非负数均为零。
要点6 数形结合题
数形结合是解决数学问题常用的思想方法,解题时必须通过所给图形抓住相关数的信息。
要点7 与二次根式有关的探究题
这类题目需要我们细心观察及思考,探究其中的规律,寻找解决问题的途径。
三、考查要点
1、利用平方根、算术平方根、立方根的定义与性质解题
(1)如果某数的一个平方根是-6,那么这个数为________.
2、考查实数的有关概念及实数大小的比较
(2)比较大小:7 .(填“>”、“=”或“<”)
3、考查二次根式的概念
(3)根号x-1 在实数范围内有意义,则x的取值范围是( )
(A)x>1 (B)x≥l (C)x<1 (D)x≤1
4、考查同类二次根式
分析:掌握同类二次根式的概念是解决此类问题的关键。首先要把能化简的二次根式化成最简二次根式,再分别看被开方数是否相同即可。
5、考查二次根式的化简与运算
(4)化简的结果是( )
A.10 B.2 C.4 D.20
四、考试易错点
1、对平方根、算术平方根、立方根的概念与性质理解不透
理解不透平方根、算术平方根、立方根的概念与性质,往往出现以下错误:求一个正数的平方根时,漏掉其中一个,而求立方根时,又多写一个;求算术平方根时前面加上正负号,成了平方根等等。
2、忽略平方根成立的条件
只有非负数才能开平方, 成立的条件是a≥0,这一条件解题时往往被我们忽略。
3、实数分类时只看表面形式
对实数进行分类不能只看表面形式,应先化简,再根据结果去判断。
4、二次根式的运算错误
在进行二次根式的运算时要注意运算法则与公式的正确应用,千万不要忽略公式的应用条件。
五、平方根和立方根考点例析
在中考试题中,平方根和立方根的考点有以下几个方面:
一、平方根的概念
如果一个数的平方等于A,那么这个数叫做A的平方根.
例1.9的平方根是【 】
(A) 3 (B) (C) 81 (D)
例2.(-5)2的平方根是【 】
(A)5 (B)-5 (C)±5 (D)±
例3.的平方根是【 】
(A) ±9 (B) ±3(C)9 (D)3
二、算术平方根
正数A的正的平方根叫做A的算术平方根.
例4.| -4|的算术平方根是【 】
(A)2 (B)±2 (C)4 (D) ±4
例5.设为正整数,若是完全平方数,则它前面的一个完全平方数是 【 】
(A) (B) (C) (D)
三、立方根
如果一个数的立方等于A,那么这个数叫做A的立方根.
例6.立方根等于3的数是【 】
(A)9 (B) (C)27 (D)
例7.等于 【 】
(A) (B) (C)3 (D)-3
例8.的值为【 】
(A)3.049 (B)3.050 (C)3.051 (D)3.052
四、科学计算器的应用
例9.用计算器计算的按键顺序是______,结果等于_____.
(5)有算术平方根的数是有理数. ( )
(6)0是最小的实数. ( )
(7)无限小数都是无理数. ( )
(8)带根号的数都是无理数. ( )
(9)不带根号的数都是有理数.( )
(10)两个无理数的和为无理数. ( )
特别注意
1、平方根是其本身的数是0;算术平方根是其本身的数是0和1;立方根是其本身的数是0和±1。
2、每一个正数都有两个互为相反数的平方根,其中正的那个是算术平方根;任何一个数都有唯一一个立方根,这个立方根的符号与原数相同。
3、本身为非负数,有非负性,即≥0;有意义的条件是a≥0。
4、公式:⑴()2=a(a≥0);⑵=(a取任何数)。
5、区分()2=a(a≥0),与 =
6.非负数的重要性质:若几个非负数之和等于0,则每一个非负数都为0(此性质应用很广,务必掌握)。
7.易混淆的三个数:(1)(2)(3)









