


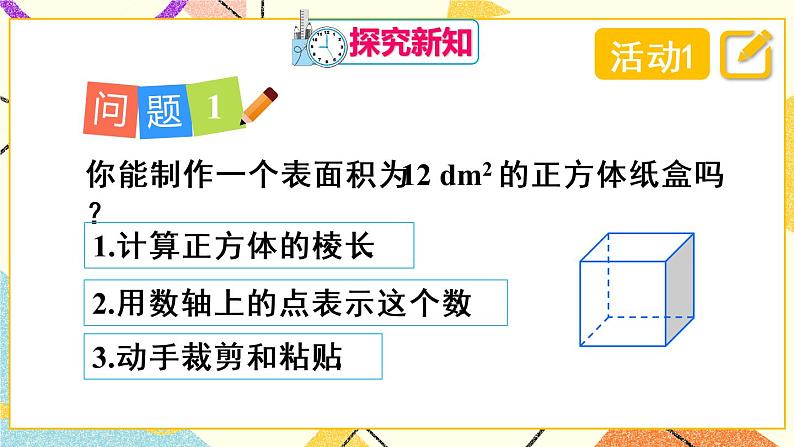
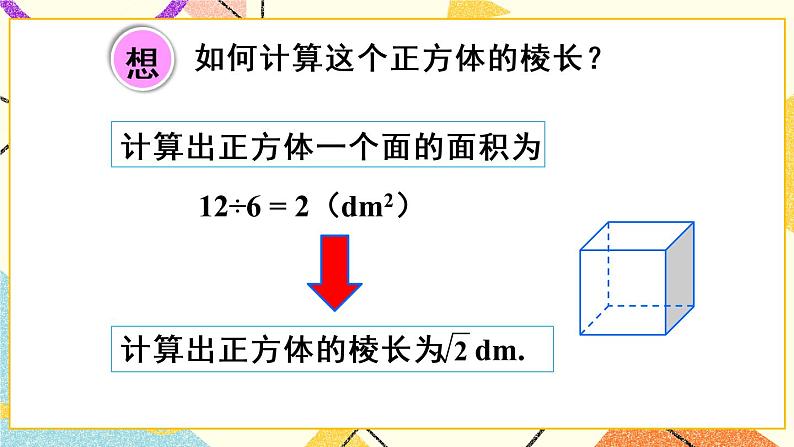


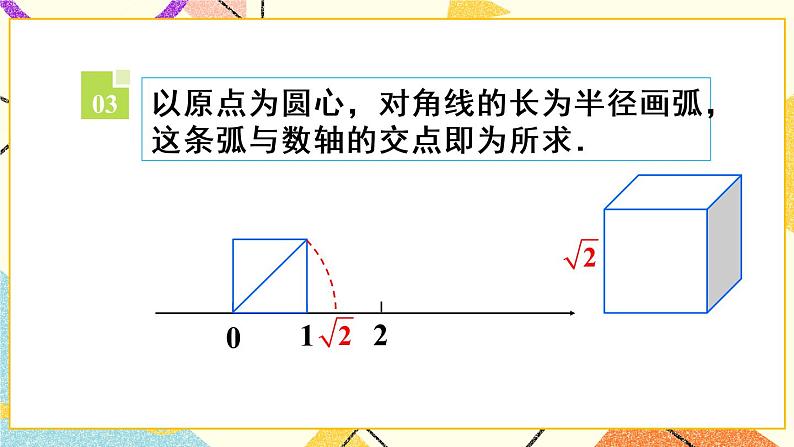

- 6.3.1《 实数》(第1课时)课件+教案+导学案 课件 7 次下载
- 6.3.2《 实数的运算》(第2课时)课件+教案+导学案 课件 8 次下载
- 6《章末复习》课件+教案+导学案 课件 9 次下载
- 7.1.1《有序数对》课件+教案+导学案 课件 10 次下载
- 7.1.2《 平面直角坐标系》课件+教案+导学案 课件 11 次下载
6《数学活动》课件+教案+导学案
展开数学活动
——求完全立方数的立方根
一、导学
1.导入课题:
我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上一道智力题:一个数是59319,希望求它的立方根.华罗庚脱口而出:39.你知道华罗庚是怎样迅速准确地计算出来的吗?这节课我们就来研究这个问题.
2.学习目标:
(1)会求完全立方数的立方根.
(2)勤于动脑,善于归纳,学习领会那些常见计算技巧,提高运算能力.
3.学习重、难点:求完全立方数的立方根的方法和步骤.
4.自学指导:
(1)自学内容:课本P59活动2.
(2)自学时间:8分钟.
(3)自学要求:按课本中问题的指引,个个击破,然后归纳总结.
(4)自学提纲:
①∵103=1000,1003=1000000并且1000<59319<1000000,
∴10<<100,∴是两位数
②13=1,23=8,33=27,43=64,53=125,63=216,73=343,83=512,93=729,103=1000,分析它们的个位数的特点,可知的个位数是9.
③把59319的后三位数319划去得59,∵27<59<64,∴确定出的十位数是3,即=39.
④已知19683,110592都是完全立方数,按上面的方法求得:
=27,=48
⑤你能归纳出求完全立方数的立方根的一般步骤吗?
⑥你能依照上面的方法求完全平方数1369,6724的算术平方根吗?
答案:37;82.
二、自学
同学们可结合自学指导进行自主学习.
三、助学
1.师助生
(1)明了学情:教师深入课堂,了解学生的自学进度和存在的问题.
(2)差异指导:根据学情进行相应指导.
2.生助生:小组内相互交流,订正纠错,互帮互学.
四、强化
1.各小组展示各自的学习成果,归纳出求完全立方数的立方根的一般步骤.
2.如果a>b,那么>,利用它可求一个立方根的近似值.
如求的近似值:
∵13=1,23=8而1<5<8,
∴1<<2.
∵1.73=4.913,1.83=5.832而4.913<5<5.832,
∴1.7<<1.8,
∵1.703=4.913,1.713=5.000211而4.913<5<5.000211,
∴1.70<<1.71.
…
如此进行下去,可以得到的更精确的近似值.
五、评价
1.学生的自我评价:回顾整个活动过程,反思自己有哪些收获和不足.
2.教师对学生的评价:
(1)表现性评价:教师根据本活动中学生的表现:是否积极参与活动,是否有独到的发现(利用这种方法能否求立方根是三位或三位以上的数,能否把这种方法迁移用来求完全平方数的平方根等),以及学习效果如何等予以评价.
(2)纸笔评价:课堂评价检测.
3.教师的自我评价(教学反思):
在本节课教学过程中,通过教学活动2,调动了学生的积极性,引导学生观察思考,逐步质疑,逐渐由旧知归纳出新知,既培养学生的动手能力,又为实数学习打下基础.
(时间:12分钟满分:100分)
一、基础巩固(60分)
1.(15分)已知4096,39304,140608都是完全立方数,不用计算器求=16,=34,=52.
2.(15分)已知=1.603,=3.454,=7.441,则=0.7441,=34.54.
3.(15分)已知=2.030,=6.419,则=0.6419, =203.0.
4.(15分)已知2304,7225,15129都是完全平方数,不用计算器求=48,=85,=123.
二、综合运用(20分)
5.求的近似值(精确到0.01).
解:∵23=8,33=27,而8<10<27,
∴2<<3.
∵2.13=9.261,2.23=10.648,而9.261<10<10.648,
∴2.1<<2.2
∵2.153=9.938375,2.163=10.077696,而9.938375<10<10.077696,
∴2.15<<2.16.
∵2.1543=9.993948,2.1553=10.007874,而2.1543更接近10.
∴≈2.15.
三、拓展延伸(20分)
6.从图书、网络等方面搜集一些巧算立方根或平方根的资料,与同学们分享一下.









