人教A版高中数学必修第一册第5章三角函数5-5-1第1课时两角差的余弦公式课件

这是一份人教A版高中数学必修第一册第5章三角函数5-5-1第1课时两角差的余弦公式课件，共28页。

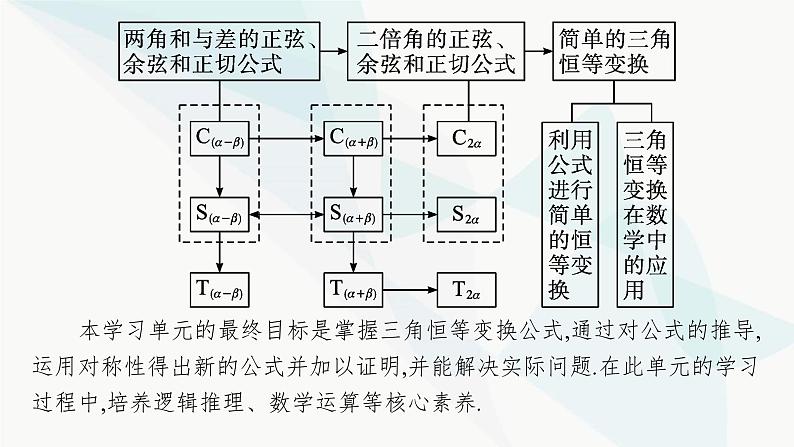
第五章5.5.1　第1课时　两角差的余弦公式基础落实·必备知识全过关重难探究·能力素养全提升目录索引 学以致用·随堂检测全达标学习单元5　三角恒等变换 本单元分为两部分,第一部分是两角和与差的正弦、余弦和正切公式;第二部分是简单的三角恒等变换.在学习过程中,我们一方面要通过公式推导获得新的公式,另一方面要利用获得的公式进行恒等变形,习惯上称为三角恒等变换.学习过程中,应逐步体会单元内容的研究路径:特殊→一般→证明公式→公式变形→新公式→公式应用.这也是我们学习本单元的知识明线.本单元具体内容结构如图所示: 本学习单元的最终目标是掌握三角恒等变换公式,通过对公式的推导,运用对称性得出新的公式并加以证明,并能解决实际问题.在此单元的学习过程中,培养逻辑推理、数学运算等核心素养.基础落实·必备知识全过关知识点:两角差的余弦公式公式:cos(α-β)=cos αcos β+sin αsin β.(1)简记符号:C(α-β).(2)适用条件:公式中的角α,β是任意角.名师点睛1.公式可简记为:余余正正、符号反.2.公式中的α,β都是任意角,既可以是一个角,也可以是几个角的组合,公式右端展开式为角α,β的同名三角函数积的和,即差角余弦等于同名积之和.3.要注意公式的逆用和变形应用,如cos(α+β)cos β+sin(α+β)sin β=cos [(α+β)-β]=cos α.微思考对于任意实数α,β,cos(α-β)=cos α-cos β都不成立吗?提示 虽然两角差的余弦公式为cos(α-β)=cos αcos β+sin αsin β,但并不说明对于任意实数α,β,cos(α-β)=cos α-cos β都不成立.例如重难探究·能力素养全提升问题2对于问题1进行一般化处理,对于任意角α,β,可否构造出(α-β),并利用角α,β的三角函数值,求出cos(α-β)的值?探究点一 利用两角差的余弦公式解决给角求值问题问题3已知两角差的余弦公式为cos(α-β)=cos αcos β+sin αsin β.对于公式,可以如何运用?【例1】 求下列各式的值:规律方法　两角差的余弦公式常见题型及解法(1)两特殊角之差的余弦值,利用两角差的余弦公式直接展开求解.(2)含有常数的式子,先将系数转化为特殊角的三角函数值,再利用两角差的余弦公式求解.(3)求非特殊角的三角函数值,把非特殊角转化为两个特殊角的差,然后利用两角差的余弦公式求解.探究点二 利用两角差的余弦公式解决给值求值问题问题4两角差的余弦公式的应用需要知道两个角的正弦及余弦值,如果只知道正弦及余弦中的某一个,该如何处理?需要解决什么问题?问题5如何来看待已知角与所求角?如何用已知角来表示所求角?规律方法　给值求值的解题策略(1)已知某些角的三角函数值,求另外一些角的三角函数值,要注意观察已知角与所求表达式中角的关系,适当地拆角与凑角,虽然有时已知角是一个复角,但应学会用数学的眼光来看成一个整体.(2)由于角的和、差与单角是相对的,因此解题过程中可以根据需要灵活地进行拆角或凑角的变换.常见角的变换有:①α=(α-β)+β;② ;③2α=(α+β)+(α-β);④2β=(α+β)-(α-β).探究点三 利用两角差的余弦公式解决给值求角问题问题6两角差的余弦公式得到的是两角差的余弦,根据此余弦值可否求出两角差?可能会遇到什么困难?如何解决?【例3】 已知α,β均为锐角,且 ,求α-β的值.延伸探究本例中,若将条件“α,β均为锐角”改为“α,β∈( ,π)”,再求α-β的值.规律方法　解决三角函数给值求角问题的方法步骤(1)确定角的范围,根据条件确定所求角的范围;(2)求所求角的某种三角函数值,为防止增解,最好选取在上述范围内单调的三角函数;(3)结合三角函数值及角的范围求角.学以致用·随堂检测全达标12341.(例1对点题)化简下列各式:(1)cos(θ+21°)cos(θ-24°)+sin(θ+21°)sin(θ-24°);解 原式=cos [θ+21°-(θ-24°)]=cos 45°= . (2)-sin 167°sin 223°+sin 257°sin 313°; 解 原式=-sin(180°-13°)sin(180°+43°)+sin(180°+77°)sin(360°-47°)=sin 13°sin 43°+sin 77°sin 47°=sin 13°sin 43°+cos 13°cos 43°=cos(13°-43°)=cos(-30°)= .1234123412343.(例2对点题)若α,β均为锐角,且 ,则cos β的值等于　　　　　. 12344.(例3对点题)若 ,且α,β均为锐角,α<β,求α+β.1234