人教A版高中数学必修第一册第5章三角函数5-1-2弧度制课件

这是一份人教A版高中数学必修第一册第5章三角函数5-1-2弧度制课件，共31页。
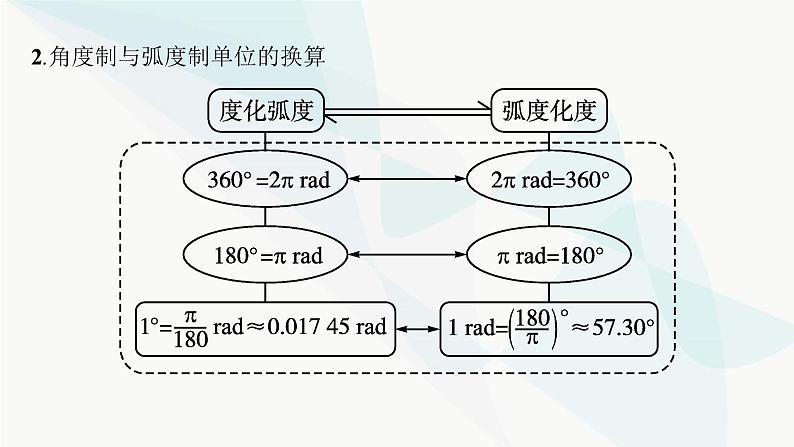
第五章5.1.2　弧度制基础落实·必备知识全过关重难探究·能力素养全提升目录索引 学以致用·随堂检测全达标基础落实·必备知识全过关度弧度半径长rad微思考在大小不同的圆中,长度为1的弧所对的圆心角相等吗?提示 不相等.因为弧长等于1,在大小不同的圆中,由于半径不同,圆心角也不同. 知识点二:弧度数的计算1.弧度数的计算(1)正角:正角的弧度数是一个　　　　. (2)负角:负角的弧度数是一个　　　　. (3)零角:零角的弧度数是　　　. (4)在半径为r的圆中,弧长为l的弧所对的圆心角为α rad,那么|α|= .正数负数02.角度制与弧度制单位的换算 3.一些特殊角与弧度数的对应关系 名师点睛度数× =弧度数,弧度数× =度数.微思考“1弧度的角”的大小和所在圆的半径大小有关吗?提示 无关,无论圆的半径多大,根据弧度制的定义:所以,“1弧度的角”的大小和所在圆的半径大小无关.知识点三:扇形的弧长和面积公式设扇形的半径为R,弧长为l,α为其圆心角,则微思考如何得到扇形的弧长与面积公式?αR 重难探究·能力素养全提升问题1研究周期变化现象,需要建立任意角的三角函数.若角的度量采用角度制,一是与函数的要求(实数单位)不符;二是与现实生活中表示周期现象的自变量也不相符,比如潮汐现象、简谐振动的自变量是时间等;因此,如何把角的度量从角度制转化成以实数单位来度量非常必要.问题2根据初中学过的弧长公式,探索弧长、半径与角度之间的关系,可否找到用实数来表示角度的方式?探究点一 弧度制的概念问题3如何从多个角度理解弧度制?【例1】 (多选题)下列说法中正确的是(　　 )A.角的弧度数与实数之间建立了一一对应的关系B.1度的角是周角的 ,1弧度的角是周角的C.根据弧度的定义,180°一定等于π弧度D.无论是用角度制还是用弧度制度量角,角的大小均与圆的半径的大小有关ABC解析 无论是用角度制还是用弧度制度量角,角的大小均与圆的半径的大小无关,故D项错误.规律方法　1.不管是以“弧度”还是以“度”为单位的角的大小都是一个与圆的半径的大小无关的定值.2.用角度制和弧度制度量零角,单位不同,但数量相同(都是0);用角度制和弧度制度量任一非零角,单位不同,数量也不同.3.以弧度为单位表示角的大小时,“弧度”或“rad”通常省略不写,但以度为单位表示角的大小时,“度”或“°”不能省去.4.以弧度为单位度量角时,常把弧度数写成nπ(n∈R)的形式.若无特别要求,不必把π写成小数,如45°= rad,不必写成45°≈0.785 rad.探究点二 角度与弧度的互化与应用问题4弧度制与角度制都是度量角的不同的单位制,也即度量角的两种不同方式,两者之间必然可以互相转化.角度与弧度如何互相转化?【例2】 (1)①将112°30'化为弧度为　　　　　. ②将 rad化为角度为　　　　　. -75° 规律方法　角度制与弧度制互化的关键与方法(1)关键:抓住互化公式π rad=180°是关键.(3)角度化弧度时,应先将分、秒化成度,再化成弧度.探究点三 用弧度表示角或范围问题5如何用弧度来表示角的大小或范围?【例3】 用弧度表示终边落在图中所示阴影部分内(不包括边界)的角的集合.分析 先将边界角由角度化为弧度,再根据阴影部分写出角的集合. 规律方法　用弧度制表示角应注意的问题(1)用弧度制表示区域角,实质是角度表示区域角在弧度制下的应用,必要时,需进行角度与弧度的换算.注意单位要统一,角度数与弧度数不能混用.(2)在表示角的集合时,可以先写出0~2π内的角,再加上2kπ,k∈Z.(3)终边在同一直线上的角的集合可以合并为{x|x=α+kπ,k∈Z},一定要做到准确无误.探究点四 弧长公式与扇形面积公式的应用问题6弧长及扇形的面积计算初中曾经学过,可否尝试用弧度来计算?与初中用角度表示的公式相比,有何优点?【例4】 (1)已知扇形的周长为8 cm,圆心角为2,求该扇形的面积;解 设扇形的半径为r cm,弧长为l cm,由圆心角为2 rad,依据弧长公式可得l=2r,从而扇形的周长为l+2r=4r=8,解得r=2,则l=4.(2)已知扇形的周长为10 cm,面积等于4 cm2,求其圆心角的弧度数. 延伸探究本例(1)中,将条件“圆心角为2”去掉,求扇形面积的最大值.规律方法　弧度制下有关弧长、扇形面积问题的解题策略(1)扇形的弧长公式和面积公式涉及四个量:面积S、弧长l、圆心角α、半径r.已知其中的三个量一定能求得第四个量,已知其中的两个量能求得剩余的两个量(通过方程组求得).(2)在研究有关扇形的相关量的最值时,往往转化为二次函数的最值问题.(3)注意扇形圆心角弧度数的取值范围是(0,2π),实际问题中注意根据这一范围进行取舍.学以致用·随堂检测全达标12341.(例1对点题)下列说法正确的是(　　)A.1弧度是长度等于半径的弧B.1弧度是1°的圆心角所对的弧C.1弧度是长度等于半径长的圆弧所对的圆心角D.1弧度等于1°C解析 1弧度角的定义:长度等于半径长的圆弧所对的圆心角叫做1弧度的角.由题意可知,只有C正确.12342.(例2对点题)(1)将-157°30'化成弧度为　　　　　. (2)将- rad化为度是　　　　　. -396° 12343.(例3对点题)以弧度为单位,写出终边落在直线y=-x上的角的集合. 12344.(例4对点题)若2弧度的圆心角所对的弧长是4 cm,则这个圆的半径r=　　　　　,圆心角所在的扇形面积是　　　　　. 2 cm　4 cm2