江苏专版2023_2024学年新教材高中数学第3章不等式章末总结提升课件苏教版必修第一册

这是一份江苏专版2023_2024学年新教材高中数学第3章不等式章末总结提升课件苏教版必修第一册，共27页。

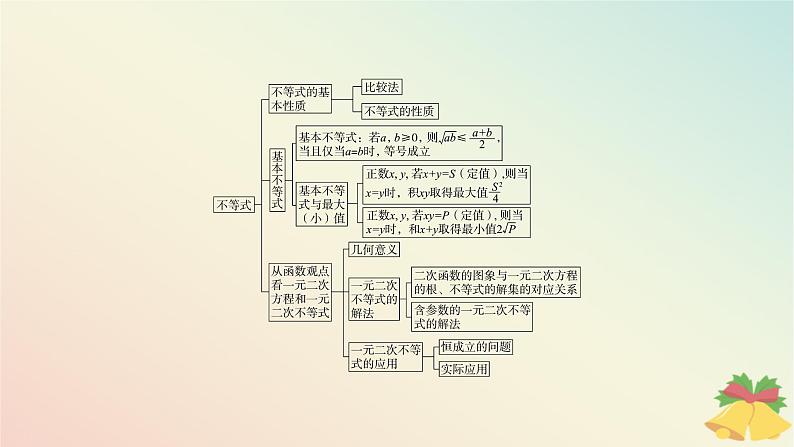
1网络构建·知识导图2要点归纳·典例提升01网络构建·知识导图02要点归纳·典例提升要点一 不等式的性质及应用 1.不等式的性质常用来比较大小、判断命题真假和证明不等式,常结合特殊值法进行判断. 2.掌握不等式的性质,重点提升数学抽象和逻辑推理的核心素养.【典例1】（1） （多选题）下列说法正确的是( ) BD     规律方法 不等式性质的应用方法 （1）作差法比较大小的关键是对差式进行变形，变形的方法一般是通分、分解因式、配方等. （2）不等式真假的判断，要依靠其适用范围和条件来确定，举反例是判断命题为假的一个好方法，用特例法验证时要注意，适合的不一定对，不适合的一定错，故特例只能否定选择项.    要点二 利用基本不等式求最值  2.借助基本不等式的应用，提升数学抽象和数学运算素养. C       CA.4 B.5 C.24 D.25 要点三 一元二次不等式的解法 1.对于一元二次不等式（分式不等式）首先转化为标准形式（不等式右侧为0,二次项系数为正）,然后能分解因式的变为因式相乘的形式,最后得到不等式的解集. 2.借助不等式的解法,培养逻辑推理和数学运算的核心素养. B     题后反思 对于含参数的一元二次不等式，若二次项系数为常数，则可先考虑分解因式，再对参数进行讨论；若不易分解因式，则可对判别式分类讨论，分类要不重不漏. B  要点四 不等式在实际问题中的应用 1.不等式的应用题常以函数为背景,多是解决现实生活、生产中的优化问题,在解题中主要涉及不等式的解法、基本不等式求最大（小）值,根据题设条件构建数学模型是关键. 2.利用不等式解决实际应用问题,提升数学建模和数学运算的核心素养.