2022--2023学年人教版八年级数学下册期末试卷（含答案）

这是一份2022--2023学年人教版八年级数学下册期末试卷（含答案），共19页。试卷主要包含了单选题，填空题等内容，欢迎下载使用。

一、单选题（10小题，共40分）
1．某学校举行了“重视阅读教学，提高核心素养”系列活动，在增大课堂阅读的同时还鼓励同学进行大量的课后阅读.王老师调查了上个月全班学生阅读课外图书的本数，统计结果如下表所示，则在本次调查中，全班学生阅读课外图书本数的平均数和众数分别是（ ）
A．1.6，1B．1，1.5C．1.6，1.5D．1，1
2．一次函数y=-3x+2的图象不经过( )
A．第一象限B．第二象限C．第三象限D．第四象限
3．下列四个二次根式中，最简二次根式是（ ）
A．B．C．D．
4．下列平面直角坐标系中的图象，不能表示y是x的函数的是（ ）
A． B． C． D．
5．已知在中，，，的对边分别记为，，，则下列条件不能判定为直角三角形的是（ ）
A．B．
C．D．
6．如图，在长方形ABCD中，，，对角线AC的垂直平分线分别交AD、AC于点M，N，连接CM，则CM的长为（ ）
A．B．C．D．5
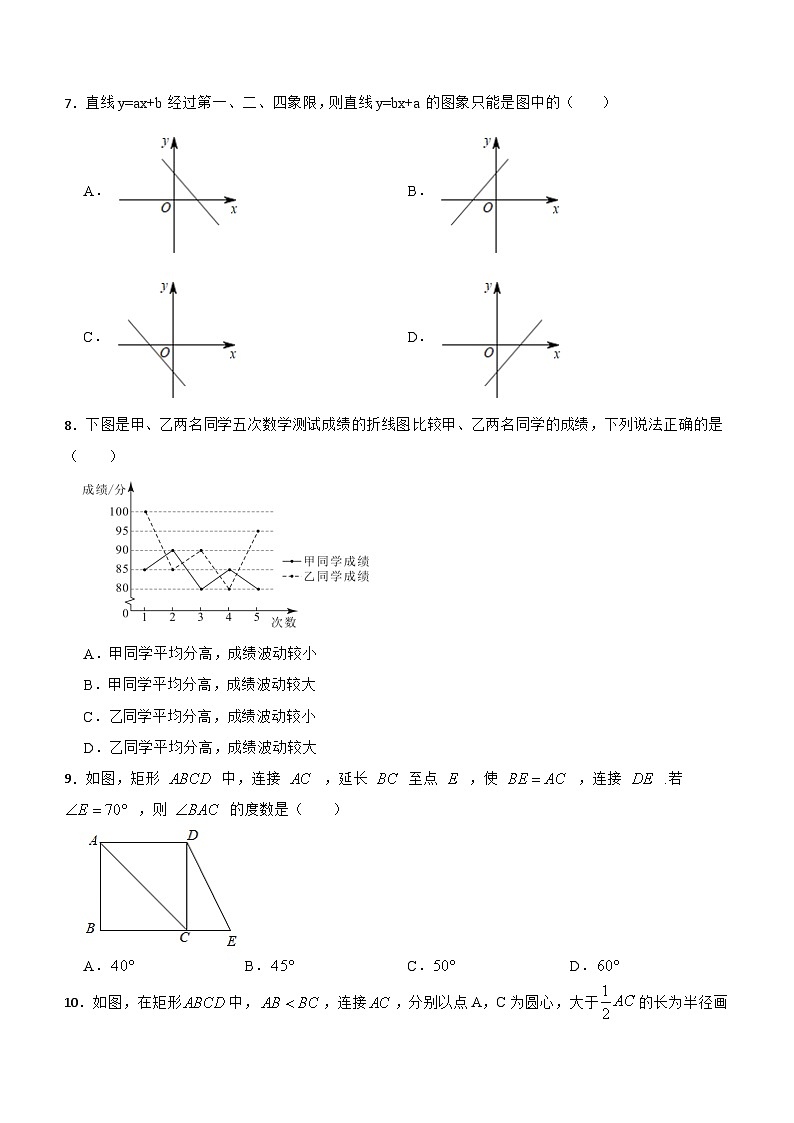
7．直线y=ax+b经过第一、二、四象限，则直线y=bx+a的图象只能是图中的（ ）
A．B．
C．D．
8．下图是甲、乙两名同学五次数学测试成绩的折线图.比较甲、乙两名同学的成绩，下列说法正确的是（ ）
A．甲同学平均分高，成绩波动较小
B．甲同学平均分高，成绩波动较大
C．乙同学平均分高，成绩波动较小
D．乙同学平均分高，成绩波动较大
9．如图，矩形 中，连接 ，延长 至点 ，使 ，连接 .若 ，则 的度数是（ ）
A．B．C．D．
10．如图，在矩形中，，连接，分别以点A，C为圆心，大于的长为半径画弧，两弧交于点M、N，直线分别交于点E、F、下列说法不一定正确的是（ ）
A．B．
C．D．
二、填空题（4小题，共20分）
11．计算： = ．
12．函数 中自变量的取值范围是
13．如图，菱形ABCD的周长为36cm，对角线AC、BD相交于O点，E是AD的中点，连接OE，则线段OE的长等于 ．
14．如图，已知 和 的图象交于点P，根据图象可得关于X、Y的二元一次方程组 的解是 .
三、（2小题，共16分）
15．先化简再求值：当a＝时，求a+ 的值．
16．如图，一架云梯长25米，斜靠在一面墙上，梯子靠墙的一端距地面24米。如果梯子的顶端下滑了4米，那么梯子的底部在水平方向也滑动了4米吗？
四、（2小题，共16分）
17．如图，在▱ABCD中，E、F分别为边AD、BC的中点，对角线AC分别交BE，DF于点G、H．求证：AG=CH．
18．如图，在菱形ABCD中，对角线AC与BD相交于点O，AC＝8，BD＝6，OE⊥BC，垂足为点E，求OE的长.
五、（2小题，共20分）
19．在平面直角坐标系 中，一次函数 为常数，且 ）的图象经过点 .
（1）求一次函数的解析式；
（2）无论 取何值，一次函数 为常数，且 ）的图象必经过一个固定的点 .
①求点 的坐标；
②在 轴上是否存在一点 使得 是等腰三角形?若存在，请求出所有符合条件的点 的坐标；若不存在，请说明理由.
20．如图，在正方形ABCD中，E、F分别是边AB、BC的中点，连接AF、DE相交于点G，连接CG．
（1）求证：AF⊥DE；
（2）求证：CG=CD．
六、（2小题，共24分）
21．“聚焦双减，落实五项管理”，为了解双减政策实施以来同学们的学习状态，某校志愿
者调研了七，八年级部分同学完成作业的时间情况．从七，八年级中各抽取20名同学作业完成时间数据（单位：分钟）进行整理和分析，共分为四个时段（x表示作业完成时间，取整数）；；；；，完成作业不超过80分钟为时间管理优秀，下面给出部分信息：
七年级抽取20名同学的完成作业时间：55，58，60，65，64，66，60，60，78﹐
78，70，75，75，78，78，80，82，85，85，88.
八年级抽取20名同学中完成作业时间在时段的所有数据为：72，75，74，76，75，75，78，75．
七，八年级抽取的同学完成作业时间统计表：
根据以上信息，解答下列问题：
（1）填空： ， ，并补全统计图；
（2）根据以上数据分析，双减政策背景的作业时间管理中，哪个年级落实得更好？请说明理由；（写出一条即可）
（3）该校七年级有900人，八年级有700人，估计七，八年级时间管理优秀的共有多少人？
22．如图，在笔直的公路旁有一座山，从山另一边的处到公路上的停靠站的距离为，与公路上另一停靠站的距离为，停靠站、之间的距离为，为方便运输货物现要从公路上的处开凿隧道修通一条公路到处，且．
（1）请判断的形状？
（2）求修建的公路的长．
七、（共1小题，14分）
23．如图，在▱ABCD中，对角线AC、BD交于点O，E是AD上一点，连接EO并延长交BC于点F，连接AF、CE，EF平分∠AEC．
（1）求证：四边形AFCE是菱形．
（2）若∠DAC=60°，EF=4，求四边形AFCE的面积．
答案解析
1．【答案】A
【解析】【解答】平均数为
由表格可得，本数为1的人数最多，即众数为1，
故答案为：A.
【分析】利用平均数和众数的定义及计算方法求解即可。
2．【答案】C
【解析】【解答】解：因为解析式y=-3x+2中，-3＜0，2＞0，图象过一、二、四象限，故图象不经过第三象限.
故答案为：C.
【分析】根据k=-3＜0，可得图象过二、四象限，根据b=2＞0，可得图象交y轴于正半轴，据此判断即可.
3．【答案】B
【解析】【解答】解：＝2，因此不符合题意；
符合最简二次根式的定义，因此符合题意；
的被开方数是小数，因此不是最简二次根式；
的被开方数是分数，因此不是最简二次根式.
故答案为：B.
【分析】最简二次根式满足两个条件：①被开方数中不含分母，②被开方数中不能含有开方开的尽的因数或因式，据此解答即可.
4．【答案】D
【解析】【解答】解：由图象，得
D的图象不满足对于x的每一个取值，y都有唯一确定的值与之对应关系，
故答案为：D.
【分析】利用函数的定义，对各选项逐一判断即可.
5．【答案】D
【解析】【解答】解：A、∵，，
∴，∴，
∴为直角三角形，不符合题意；
B、∵，
设， 则，
∴，
∴，不符合题意；
C、，为直角三角形，不符合题意；
D、∵，
∴设，
∴，解得，
∴，
∴不是直角三角形，符合题意；
故答案为：D．
【分析】利用勾股定理的逆定理和三角形的内角和逐项判断即可。
6．【答案】D
【解析】【解答】解：∵四边形ABCD是矩形，
∴∠D=∠B=90°，AD=BC=8，AB=DC=4，
∵MN是AC的垂直平分线，
∴AM=CM，
∴DM=AD-AM=AD-CM=8-CM，
在Rt△DMC中，由勾股定理得：DM2+DC2=CM2，
（8-CM）2+42=CM2，
解得：CM=5，故D符合题意．
故答案为：D．
【分析】根据线段垂直平分线的性质求出AM=CM，再利用勾股定理计算求解即可。
7．【答案】D
【解析】【解答】解：∵直线y＝ax+b经过第一、二、四象限，
∴a＜0，b＞0，
∴直线y＝bx+a的图象经过第一、三、四象限，
故答案为：D．
【分析】一次函数y=kx+b（k≠0），当k＞0，b＞0时， 一次函数图象经过第一、二、三象限；当k＞0，b＜0时， 一次函数图象经过第一、三、四象限；当k＜0，b＞0时， 一次函数图象经过第一、二、四象限；当k＜0，b＜0时， 一次函数图象经过第二、三、四象限；据此判断即可.
8．【答案】D
【解析】【解答】解：由题意得，
∴，
∴乙同学平均分高，成绩波动较大，
故答案为：D
【分析】根据平均数和方差的计算方法结合题意即可求解。
9．【答案】C
【解析】【解答】解：连接 ，交 于 ，如图：
四边形 是矩形，
， ， ， ，
，
，
，
，
，
，
.
故答案为：C.
【分析】连接BD，交AC于O，由矩形的性质可得∠ABC=90°，OA=OC=OB=OD，由等腰三角形的性质可得∠BAC=∠OBA，由BE=AC可得BE=BD，结合等腰三角形的性质可得∠BDE=∠E=70°，根据内角和定理求出∠DBE的度数，据此解答.
10．【答案】A
【解析】【解答】根据作图步骤及方法可得MN是AC的垂直平分线，
∴AE=CE，AF=CF，AC⊥EF，
∴∠CAF=∠ACB，∠AOE=90°，
∴∠CAE+∠AEF=90°，
故C不符合题意；
∵∠AFB=∠CAF+∠ACB，
∴∠AFB=2∠ACB，
故B不符合题意；
设AC与MN的交点为点O，如图：
∵∵四边形ABCD是矩形，
∴AD//BC，
∴∠EAO=∠FCO，
∵∠AOE=∠COF，AO=CO，
∴△AOE≌△COF（ASA），
∴AE=FC，
∴CE=AE=CF，
故D不符合题意；
根据题干中的条件无法证出∠BAF=∠CAF，
故A符合题意；
故答案为：A.
【分析】利用垂直平分线的性质，全等三角形的判定及性质，角的运算及等量代换逐项判断即可。
11．【答案】
【解析】【解答】解：
故答案为： ．
【分析】利用二次根式的除法法则进行计算。
12．【答案】x≤2且x≠1
【解析】【解答】解：根据题意得：
且x−1≠0，
解得： 且
故答案为 且
【分析】观察含自变量的式子含有分式和二次根式，可知被开方数是非负数且分母不等于0，可建立关于x的不等式组，然后求出不等式组的解集.
13．【答案】 cm
【解析】【解答】解：∵菱形ABCD的周长为36cm，
∴CD= =9cm．
∵四边形ABCD为菱形，且AC与BD交点为O，
∴O为AC的中点，
又∵E是AD的中点，
∴OE为△ACD的中位线，
∴OE= CD= cm．
故答案为： cm．
【分析】根据菱形的性质四边相等，由周长求出边长，再根据菱形的对角线互相平分，得到OE为△ACD的中位线，根据中位线定理，求出OE的长.
14．【答案】
【解析】【解答】解：由图知：函数y=ax+b和y=kx的图象交于点P（﹣4，﹣2），则x=﹣4，y=﹣2同时满足两个函数的解析式，∴ 是 的解，即二元一次方程组 的解．故答案为 ．
【分析】根据一次函数与二元一次方程的关系可以知道：两函数图象的交点即是二元一次方程组的解。
15．【答案】解：∵a＝＞1，
∴原式＝a+|a﹣1|
＝a+（a﹣1）
＝2a﹣1，
当a＝时，
原式＝2﹣1
【解析】【分析】原式= a+|a﹣1| ，由于a＝＞1，可得a-1＞0，利用绝对值的性质化简即可.
16．【答案】解：由题意得此时a=24米，c=25米，根据a2+b2=c2，∴b=7米；
设滑动后梯子的底端到墙的距离为b米，得方程：b2+（24﹣4）2=252，解得：b=15，所以梯子向后滑动了8米.
综合得：如果梯子的顶端下滑了4米，那么梯子的底部在水平方向不是滑4米.
【解析】【分析】由题意得a=24米，c=25米，根据勾股定理a2+b2=c2，可求出梯子底端离墙有多远.由题意得滑动后a=20米，c=25米，由勾股定理可得出此时的b，继而能和原来的b进行比较.
17．【答案】证明：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠ADF=∠CFH，∠EAG=∠FCH，
∵E、F分别为AD、BC边的中点，
∴AE=DE= AD，CF=BF= BC，
∴DE∥BF，DE=BF，
∴四边形BFDE是平行四边形，
∴BE∥DF，
∴∠AEG=∠ADF，
∴∠AEG=∠CFH，
在△AEG和△CFH中， ，
∴△AEG≌△CFH（ASA），
∴AG=CH．
【解析】【分析】本题考查了平行四边形的性质和判定，全等三角形的判定与性质；熟练掌握平行四边形的判定与性质，证明三角形全等是解决问题的关键．根据平行四边形的性质得到AD∥BC，得出∠ADF=∠CFH，∠EAG=∠FCH，证出四边形BFDE是平行四边形，得出BE∥DF，证出∠AEG=∠CFH，由ASA证明△AEG≌△CFH，得出对应边相等即可．
18．【答案】解：∵四边形ABCD为菱形，
∴AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，
在Rt△OBC中，∵OB=3，OC=4，
∴BC==5，
∵OE⊥BC，
∴OE•BC=OB•OC，
∴OE=.
故答案为.
【解析】【分析】 由菱形的性质可得AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，在Rt△OBC中，利用勾股定理求出BC=5，根据△OBC的面积=OE•BC=OB•OC即可求出OE的长.
19．【答案】（1）解：将 代入 ，
，
，
一次函数的解析式为
（2）解：① ，
，
根据题意得 ，
，
则当 时， ，
所以 ；
②设点 ，
点 ，点 ，点 ，
， ， ，
当 时，
，
， ，
点 坐标为 ， 或 ， ；
若 时，
，
， （不合题意舍去），
点 坐标为 ；
若 时，
，
，
点 坐标为 ；
综上所述：点 的坐标为 ， 或 ， 或 或
【解析】【分析】（1）将点A坐标代入y=mx-m+4中可得m的值，据此可得一次函数解析式；
（2）①将一次函数解析式变形可得y=(x-1)m+4，由题意可得x-1=0，求出x的值，进而得到y的值，据此可得点B的坐标；
②设P（x，0），由勾股定理可得AB、BP、AP，然后分AB=AP，AB=BP，AP=BP进行求解即可.
20．【答案】（1）证明:∵四边形ABCD为正方形
∴AB=BC=CD=AD，∠ABF=∠DAE=90°，
又∵E，F分别是边AB．BC的中点
∴AE= AB．BF= BC
∴AE=BF．
在△ABF与△DAE中，
，
∴△DAE≌△ABF（SAS）．
∴∠ADE=∠BAF，
∵∠BAF+∠DAG=90°，
∴∠ADG+∠DAG=90°，
∴∠DGA=90°，即AF⊥DE．
（2）证明：延长AF交DC延长线于M，
∵F为BC中点，
∴CF=FB
又∵DM∥AB，
∴∠M=∠FAB．
在△ABF与△MCF中，
∴△ABF≌△MCF（AAS），
∴AB=CM．
∴AB=CD=CM，
∵△DGM是直角三角形，
∴GC= DM＝DC．
【解析】【分析】（1）正方形ABCD中，AB=BC，BF=AE，且∠ABF=∠DAE=90°，即可证明△ABF≌△DAE，即可得∠DGA=90°，结论成立．
（2）延长AF交DC延长线于M，证明△ABF≌△MCF，说明△DGM是直角三角形，命题得证．
21．【答案】（1）解：75；78；补全频数分布直方图如下：
（2）解：七年级落实的好，理由：七年级学生完成作业的平均时间为 分，比八年级的少；
（3）解：七年级作业管理为优秀所占的比例为 ，八年级作业管理为优秀所占的比例为 ，
所以七、八年级作业管理为优秀的人数为 （人 ），
答：七，八年级时间管理优秀的共有 人．
【解析】【解答】解：（1）将八年级抽取20名同学的完成作业时间按从小到大的顺序排列后，第10，11个数均在C时段，
而C时段的所有数据为：72，75， 74 ，76，75，75，78，75，
按从小到大排列为：72，74，75，75，75，75，76，78，
则第10，11个数均为75，所以中位数 ．
将七年级抽取20名同学的完成作业时间出现次数最多的是78分，因此众数是78分，即 .
故答案为：75，78；
【分析】（1）将八年级抽取20名同学的完成作业时间按从小到大的顺序进行排列，求出中间两个数据的平均数可得中位数a的值，找出七年级抽取20名同学的完成作业时间出现次数最多的数据可得众数b的值，根据统计出的数据找出B时段的人数，据此可补全条形统计图；
（2）根据平均数的大小进行分析判断；
（3）首先分别求出样本中七、八年级作业管理为优秀所占的比例，然后分别乘以总人数即可.
22．【答案】（1）解：是直角三角形．
，，，
，
，
，
是直角三角形．
（2）解：，
，
．
答：修建的公路的长是．
【解析】【分析】（1）利用勾股定理的逆定理进行解答即可；
（2）根据即可求解.
23．【答案】（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AO=CO，
∴∠AEF=∠CFE，
在△AOE和△COF中，
，
∴△AOE≌△COF（AAS），
∴OF=OE，
∵AO=CO，
∴四边形AFCE是平行四边形；
∵EF平分∠AEC，
∴∠AEF=∠CEF，
∴∠CFE=∠CEF，
∴CE=CF，
∴四边形AFCE是菱形；
（2）解：由（1）得：四边形AFCE是菱形，
∴AC⊥EF，EO=FO=EF=2，
∴∠AOE=90°，
∵∠DAC=60°，
∴∠AEO=30°，
∴2OA=AE，
由勾股定理得，即，
∴AO=2，
∴AC=2OA=4，
∴四边形AFCE的面积=AC×EF=×4×4=8．
【解析】【分析】（1）由“AAS“证出△AOE≌△COF，得出OF=OE，证出四边形AFCE是平行四边形；再证出CE=CF，即可得出结论；
（2）根据菱形的性质得出AC⊥EF，EO=FO=EF=2，求出∠AOE=90°，根据三角形的内角和定理得出∠AEO=30°，求出AO=2，得出AC=2OA=4，根据菱形的面积公式即可得出结论。阅读课外图书的本数（本）
0
1
2
3
人数
2
18
14
6
年级
平均数
中位数
众数
七年级
72
75
八年级
75
75