初中数学人教版九年级上册24.1.1 圆一课一练

第10讲 圆的有关性质（二）

(重点题型方法与技巧)

目录

类型一：利用圆周角定理及其推论求角的度数

类型二：运用弧、弦、圆心角、圆周角的关系进行计算或证明

类型三：圆内接四边形

类型一：利用圆周角定理及其推论求角的度数

计算圆心角和圆周角时的注意事项：
1.在进行有关圆心角与圆周角的计算时，应适当添加辅助线，以方便角度之间的转化.一条弧所对的圆心角只有一个，而所对的圆周角有无数个，它们都相等；
2.一条弦所对的圆心角只有一个，但它所对的圆周角却有无数个，在同一条弦的同侧的圆周角相等，在同一条弦的异侧的两个圆周角互补.

典型例题

例题1．（2022·云南·昭通市昭阳区第一中学九年级期末）如图，AB是⊙O的直径，AC、BC是⊙O的弦，若∠A＝30°，则∠B的度数为（　　）

A．70° B．90° C．40° D．60°

例题2．（2022·湖北·五峰土家族自治县中小学教研培训中心九年级期中）如图，点A，B，C，D，E在⊙O上，AB＝CD，∠OAB＝70°，则∠CED＝（    ）

A．70° B．35° C．40° D．20°

例题3．（2022·全国·九年级单元测试）如图，四边形ABCD为⊙O的内接四边形，连接BD，若AB＝AD＝CD，∠BDC＝75°，则∠C的度数为（　　）

A．55° B．60° C．65° D．70°

例题4．（2022·福建省福州第八中学九年级阶段练习）已知A，B，C三点在⊙O上，若∠ACB＝130°，则∠AOB＝___________°．

例题5．（2022·云南·会泽县大井镇第二中学校九年级期中）如图，的弦与直径相交，若，则∠AOD=____度．

例题6．（2022·江苏·泰州市姜堰区第四中学九年级）如图，点A、B、C、D、E在上，且为，求的度数．

同类题型演练

1．（2022·全国·九年级单元测试）如图，是直径，点，在半圆上，若，则（    ）

A． B． C． D．

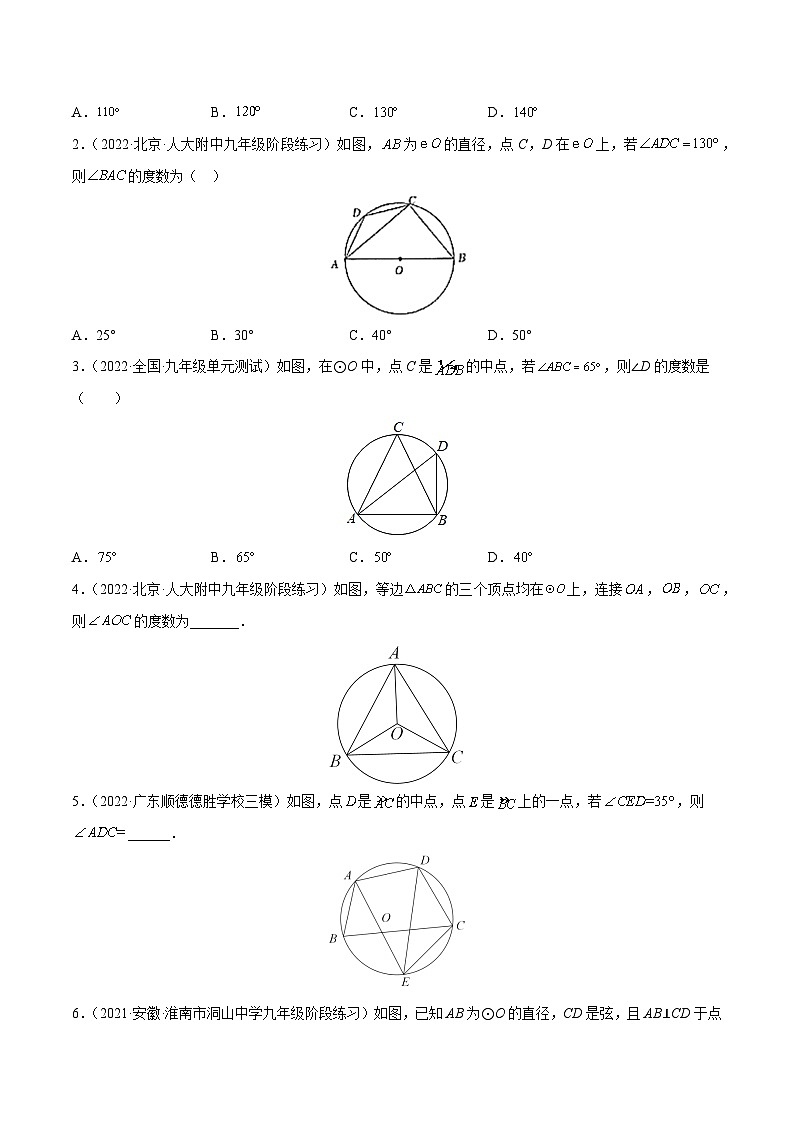
2．（2022·北京·人大附中九年级阶段练习）如图，为的直径，点C，D在上，若，则的度数为（    ）

A．25° B．30° C．40° D．50°

3．（2022·全国·九年级单元测试）如图，在⊙O中，点C是的中点，若，则∠D的度数是（　　）

A． B． C． D．

4．（2022·北京·人大附中九年级阶段练习）如图，等边的三个顶点均在上，连接，，，则的度数为_______．

5．（2022·广东顺德德胜学校三模）如图，点是的中点，点是上的一点，若，则______．

6．（2021·安徽·淮南市洞山中学九年级阶段练习）如图，已知AB为⊙O的直径，CD是弦，且AB⊥CD于点E．连接AC、OC、BC．

(1)求证：∠ACO＝∠BCD．

(2)若BE＝3，CD＝8，求BC的长．

类型二：运用弧、弦、圆心角、圆周角的关系进行计算或证明

圆中证明弧、弦、圆心角、圆周角相等或倍分关系的方法：

在圆中证明弧、弦、圆心角、圆周角的相等或倍分关系时，应从同类型元素（指弧、弦、角）的相等或倍分关系入手，转化为另一种元素的相等或倍分关系，从而得到问题的结论.

典型例题

例题1．（2022·黑龙江·哈尔滨德强学校九年级阶段练习）在中，满足=2，则下列说法正确的是（   ）

A． B． C． D．无法确定

例题2．（2022·全国·九年级课时练习）如图，A、B、C是上的三个点，，，则的度数是（    ）

A．25° B．30° C．40° D．55°

例题3．（2022·河南南阳·九年级开学考试）下列语句中：①平分弦的直径垂直于弦；②相等的圆心角所对的弧相等；③长度相等的两条弧是等弧；④圆是轴对称图形，任何一条直径都是它的对称轴；⑤在同圆或等圆中，如果两条弦相等，那么他们所对的圆周角相等，不正确的有（    ）

A．2个 B．3个 C．4个 D．5个

例题4．（2022·浙江湖州·九年级期末）如图，四边形ABCD是半圆O的内接四边形，其中AB是直径，点C是弧DB的中点，若∠C＝110°，则∠ABC的度数=______．

例题5．（2021·浙江·杭州市建兰中学九年级期中）如图，AB是的直径，四边形ABCD内接于，OD交AC于点E，AD＝CD．若AC＝10，DE＝4，则BC的长为______．

例题6．（2022·江苏·九年级）如图，正方形ABCD内接于⊙O， ，求证：BM＝CM．

同类题型演练

1．（2021·甘肃·九年级专题练习）如图，在中，，连接AC，CD，则AC与CD的关系是（    ）．

A． B．

C． D．无法比较

2．（2021·山东潍坊·二模）如图，是的直径，，是上的两点，且点为优弧的中点，连接，，，与交于点．若，则的度数为（    ）

A． B． C． D．

3．（2020·上海民办建平远翔学校九年级阶段练习）下列关于圆的说法中，错误的是（    ）

A．半径、圆心角分别相等的两段弧一定是等弧

B．如果两条弦相等，那么这两条弦所对的圆心角相等

C．圆的对称轴是任意一条直径所在的直线

D．拱形不一定是弓形

4．（2021·四川绵阳·九年级期末）如图，AB为⊙O的直径，点D是弧AC的中点，过点D作DE⊥AB于点E，延长DE交⊙O于点F，若AE＝3，⊙O的直径为15，则AC长为（　　）

A．10 B．13 C．12 D．11

5．（2022·全国·九年级课时练习）如图，点A、B、C、D均在上，若，，则∠B的度数为______．

6．（2021·浙江·温州市第十二中学九年级期中）如图， 为的直径， 点是弧的中点， 过点作于点 ， 延长 交 于点 ， 若 ， 则 的半径长为__________

7．（2021·陕西·商南县富水镇初级中学九年级期中）如图，的弦、相交于点，且．求证：．

8．（2021·黑龙江齐齐哈尔·九年级期中）如图，四边形ABCD中，∠B＝∠D，AB＝CD，AB与DC不平行，过点A作，交△ABC的外接圆⊙O于点E，连接CE、OA．

（1）求证：四边形ADCE为平行四边形；

（2）求证：AO平分∠BAE．

类型三：圆内接四边形

典型例题

例题1．（2021·重庆十八中两江实验中学九年级阶段练习）如图，四边形是的内接四边形，且，，则的度数为（    ）

A． B． C． D．

例题2．（2022·江苏·九年级单元测试）若四边形ABCD是⊙O的内接四边形，∠A：∠C＝1：2，则∠C＝（    ）

A．120° B．130° C．140° D．150°

例题3．（2022·浙江衢州·二模）如图，是的直径，C，D为上的点，且点D在弧上．若，则的度数为（    ）

A． B． C． D．

例题4．（2021·浙江·金华海亮外国语学校九年级阶段练习）如图，四边形ABCD是是内接四边形，已知，则______．

例题5．（2022·湖南·长沙麓山国际实验学校九年级阶段练习）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，∠ADC=130°，连接AC，则∠BAC的度数为___________．

例题6．（2022·云南昆明·九年级期末）如图，四边形内接于，，求证：．

同类题型演练

1．（2022·江苏盐城·九年级期末）如图，ABCD为圆内接四边形，若∠A＝60°，则∠C等于（  ）

A．30° B．60°

C．120° D．300°

2．（2022·江苏宿迁·九年级期末）在圆内接四边形中，，则等于(   )

A． B． C． D．

3．（2022·四川自贡·九年级专题练习）如图，四边形内接于⊙，为⊙的直径，，则的度数是（    ）

A．90° B．100° C．110° D．120°

4．（2022·甘肃·民勤县第六中学九年级期末）如图，已知四边形ABCD内接于⊙O，E在AD的延长线上，∠CDE=82°，则∠ABC的度数是_____．

5．（2022·浙江温州·模拟预测）如图，四边形ABCD内接于⊙O，已知∠BAD=∠BCD=90°，AD=CD，且∠ADC=120°，若点E为弧BC的中点，连接DE，则∠CDE的大小是__________．

6．（2022·江苏·九年级）如图，在△ABC中，AB＝AC，以AB为直径的圆分别交AC，BC于点D、E，过点A作AF∥BC交圆于点F，连接DE、EF．求证：

(1)四边形ACEF是平行四边形；

(2)EF平分∠BED．

9．（2022·新疆喀什·九年级期末）如图，四边形APBC内接于圆，，连接AB，PC，．

(1)是_________三角形；

(2)在PC上取一点E，使，若，，求PC的长．