初中数学人教版九年级上册23.3 课题学习 图案设计课堂检测

第08讲 中心对称 图案设计

(重点题型方法与技巧)

目录

类型一：中心对称与中心对称图形

类型二：关于原点对称的点的坐标

类型三：利用轴对称、平移、旋转设计图形

类型一：中心对称与中心对称图形

1．中心对称是指两个图形间的位置关系．

2．中心对称是特殊的旋转，旋转角为180°．

3．成中心对称的两个图形，只有一个对称中心，这个对称中心可能在每个图形的外部，也可能在每个图形的内部或图形上，但对称点一定在对称中心的两侧与对称中心重合．

典型例题

例题1．（2022·全国·九年级专题练习）下列说法中错误的是（       ）

A．成中心对称的两个图形全等

B．中心对称图形绕对称中心旋转后，都能与自身重合

C．中心对称图形的对称中心是连结对称点的线段的中点

D．成中心对称的两个图形中，连结对称点的线段被对称轴平分

例题2．（2021·四川师范大学附属中学九年级阶段练习）如图，在平面直角坐标系中，ABC的顶点A在第一象限，点B，C的坐标分别为(2，1)，(6，1)，∠BAC＝90°，AB＝AC，直线AB交y轴于点P，若ABC与关于点P成中心对称，则点的坐标为（　　）

A．(﹣4，-5) B．(﹣5，﹣4) C．(﹣3，﹣4) D．(﹣4，﹣3)

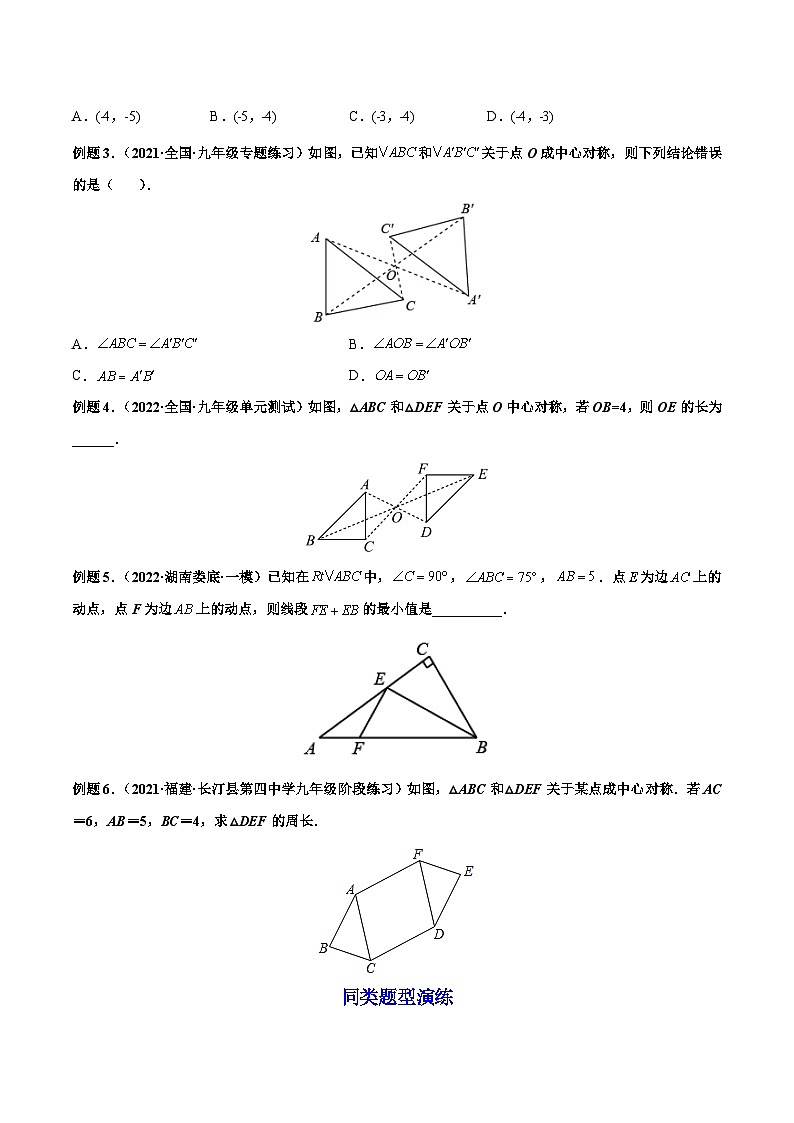
例题3．（2021·全国·九年级专题练习）如图，已知和关于点O成中心对称，则下列结论错误的是（       ）．

A． B．

C． D．

例题4．（2022·全国·九年级单元测试）如图，△ABC和△DEF关于点O中心对称，若OB=4，则OE的长为______．

例题5．（2022·湖南娄底·一模）已知在中，，，．点为边上的动点，点F为边上的动点，则线段的最小值是__________．

例题6．（2021·福建·长汀县第四中学九年级阶段练习）如图，△ABC和△DEF关于某点成中心对称．若AC＝6，AB＝5，BC＝4，求△DEF的周长．

同类题型演练

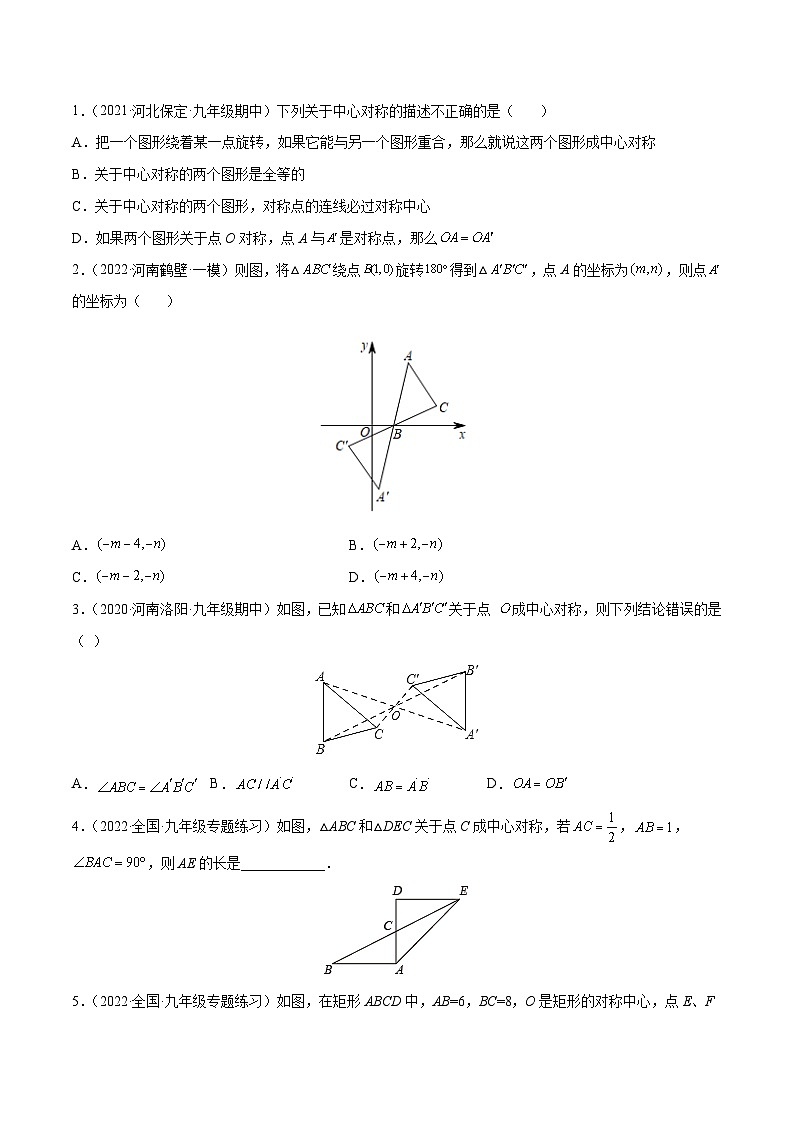
1．（2021·河北保定·九年级期中）下列关于中心对称的描述不正确的是（       ）

A．把一个图形绕着某一点旋转，如果它能与另一个图形重合，那么就说这两个图形成中心对称

B．关于中心对称的两个图形是全等的

C．关于中心对称的两个图形，对称点的连线必过对称中心 

D．如果两个图形关于点O对称，点A与是对称点，那么

2．（2022·河南鹤壁·一模）则图，将△绕点旋转得到△，点A的坐标为，则点的坐标为（       ）

A． B．

C． D．

3．（2020·河南洛阳·九年级期中）如图，已知和关于点 成中心对称，则下列结论错误的是（ ）

A． B． C． D．

4．（2022·全国·九年级专题练习）如图，△ABC和△DEC关于点C成中心对称，若，，，则AE的长是____________．

5．（2022·全国·九年级专题练习）如图，在矩形ABCD中，AB=6，BC=8，O是矩形的对称中心，点E、F分别在边AD、BC上，连接OE、OF，若AE=BF=2，则OE+OF的值为__________．

6．（2022·广东广州·九年级期末）如图，已知△ABC中，BD是中线．

(1)尺规作图：作出以D为对称中心，与△BCD成中心对称的△EAD．

(2)猜想AB+BC与2BD的大小关系，并说明理由．

7．（2021·广西·河池市宜州区教育局教学研究室九年级期中）如图，平面直角坐标系中，已知点A（-1，0），B（-4，2），C（-4，-3）

（1）画出△ABC关于原点成中心对称的图形△A1B1C1；

（2）画出△ABC绕点O顺时针旋转90°后的图形△A2B2C2 ；

（3）写出点B2和C2的坐标．

类型二：关于原点对称的点的坐标

两个点关于原点对称时，它们的坐标符号相反，即点P（x，y）关于原点的对称点为P′（–x，–y）．

典型例题

例题1．（2022·全国·九年级单元测试）在平面直角坐标系中，已知点A（－3，1）与点B关于原点对称，则点B的坐标为（    ）

A．（1，－3） B．（－1，3） C．（－3，－1） D．（3，－1）

例题2．（2022·全国·九年级专题练习）若点，关于原点对称，则m、n的值为（    ）

A．， B．，

C．， D．，

例题3．（2022·新疆·乌鲁木齐市第七十四中学九年级期末）若点A(4，n)与点B(－m，6)关于原点对称，则m＋n＝________．

例题4．（2021·广东·华中师范大学海丰附属学校九年级期中）已知点和点关于原点对称，则______．

同类题型演练

1．（2022·全国·九年级专题练习）若点A，B关于原点对称，且A(2，)，则点B的坐标为（    ）

A．(2，4) B．(，4) C．(2，) D．(，)

2．（2021·黑龙江·塔河县第一中学校九年级期中）平面直角坐标系内一点P（-a，3）与点Q（2，b）关于原点对称，则ab=（    ）

A．6 B．9 C．-6 D．-9

3．（2022·贵州安顺·九年级阶段练习）已知点在第二象限，且，则点M关于原点对称的点的坐标是（    ）

A． B． C． D．

4．（2022·福建·莆田擢英中学九年级期末）已知点A（m，2）与点B（﹣6，n）关于原点对称，则m﹣n的值为_______．

5．（2022·重庆巴南·九年级期末）若点A（，4）与点B（，）关于原点对称，则式子的值是_________．

类型三：利用轴对称设计图形

1．利用轴对称设计图案关键是要熟悉轴对称的性质，利用轴对称的作图方法来作图，通过变换对称轴来得到不同的图案．

2．确定一个基本图案按照一定的方向平移一定的距离，连续作图即可设计出美丽的图案．通过改变平移的方向和距离可使图案变得丰富多彩．

典型例题

例题1．（2022·全国·九年级专题练习）将如图所示的图案以圆心为中心，旋转180°后得到的图案是（    ）

A．B．C． D．

例题2．（2020·重庆南开（融侨）中学校九年级期末）下列大学校徽内部图案中可以看成由某一个基本图形通过平移形成的是（    ）

A． B． C． D．

例题3．（2022·全国·九年级专题练习）把18个边长都为1的等边三角形如图拼接成平行四边形，且其中6个涂上了阴影现在，可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处，使新构成的阴影部分图案是轴对称图形，共可得________种轴对称图形．

例题4．（2021·全国·九年级专题练习）如果，那么_______．

例题5．（2022·全国·九年级专题练习）如图方格中，小正方形边长为1个单位长度，每个小正方形的顶点叫做格点．请按下列要求画出一个符合题意的四边形，且顶点在格点上．

(1)在图1中画：是中心对称图形，但不是轴对称图形，且面积为8；

(2)在图2中画：既是中心对称图形又是轴对称图形，且面积为10；

(3)在图3中画：既是中心对称图形又是轴对称图形，且各边长都是无理数，面积为10．

同类题型演练

1．（2022·全国·九年级专题练习）如图，先将该图沿着它自己的右边缘翻折，再绕着右下角的一个端点按顺时针方向旋转，之后所得到的图形是（    ）

A． B．

C． D．

2．（2022·全国·九年级专题练习）在下列四种图形变换中，如图图案包含的变换是（   ）

A．平移、旋转和轴对称 B．轴对称和平移

C．平移和旋转 D．旋转和轴对称

3．（2021·全国·九年级专题练习）在综合实践活动课上，小红准备用两种不同颜色的布料缝制一个正方形座垫，座垫的图案如右图所示，应该选下图中的哪一块布料才能使其与右图拼接符合原来的图案模式 ( ).

A． B． C． D．

4．（2021·全国·九年级期末）如图，图2的图案是由图1中五种基本图形中的两种拼接而成，这两种基本图形是（　　）

A．①② B．①③ C．①④ D．③⑤

5．（2022·全国·九年级专题练习）如图，在等边三角形网格中，已有两个小等边三角形被涂黑，若再将图中其余小等边三角形涂黑一个，使涂色部分构成一个轴对称图形，则有_______种不同的涂法．

5．（2020·全国·九年级单元测试）如图，请画出一个图形经过两次轴对称变换之后得到的图形，其中图①中的两条对称轴是平行的，图②中的两条对称轴是垂直的．仔细观察上面的两个图形经过两次轴对称变换之后得到的图形．图①中的图形除经过两次轴对称变换得到之外，还可以通过我们学过的________变换得到，图②中的图形还可以通过________变换得到．

6．（2022·山西·九年级专题练习）阅读理解，并解答问题：

观察发现：

如图1是一块正方形瓷砖，分析发现这块瓷砖上的图案是按图2所示的过程设计的，其中虚线所在的直线是正方形的对称轴．

问题解决：

用四块如图1所示的正方形瓷砖按下列要求拼成一个新的大正方形，并在图3和图4中各画一种拼法．

(1)图3中所画拼图拼成的图案是轴对称图形，但不是中心对称图形；

(2)图4中所画拼图拼成的图案既是轴对称图形，又是中心对称图形．