初中数学浙教版八年级上册1.4 全等三角形一等奖教学设计

浙教版数学 八上 1.4全等三角形 教案

一、教材分析

全等三角形是几何图形部分的重要内容之一，帮助学生了解全等三角形的定义，性质，定理等内容，是对简单的平面图形的进一步研究，也是后续研究多边形的性质，三角函数等知识的基础，在平面几何中有着非常重要的地位和作用。

二、学情分析

首先是学生的知识特征，八年级的学生已经学习过点，直线，角的相关概念，前面刚刚初步认识了三角形，以及三角形的高线，中线，角平分线的对于与性质，边与角的性质。但是学生对于图形全等，三角形的全等关系还是首次遇到，需要老师积极引导。

然后是学生的心理特征，八年级的学生好奇心重，求知欲强，教师通过合适的方法引入有助于他们更好地三角形的相关内容。

三、教学目标

知识与技能

1．理解全等图形、全等三角形及全等三角形的对应元素的概念；

2．掌握全等三角形的性质及其应用；

3.会确定全等三角形的对应角和对应边

过程与方法：培养自主探究能力以及证明推理能力

情感态度与价值观：能应用全等三角形的性质进行简单的推理和解决实际问题，发现生活中的全等图形，感受数学的乐趣。

四、教学重难点

重点：全等形的概念和全等三角形的性质。

难点：理解全等三角形边、角之间的对应关系和利用概念证明两个三角形全等。

五、教学方法、手段

教学方法：讲授法，探究法，练习法

教学手段：板书与多媒体课件相结合

六．教学过程

创设情景，引出课题

观察五星红旗，你能找到形状大小都相同的五角星吗？

四个小五角星的形状大小都相同

每对图形的形状和大小都相同

经过平移旋转之后叠在一起可以重合

能够完全重合的两个图形叫做全等图形

2.如图，画在透明纸上的△ABC和△A’B’C’是全等图形吗？你是怎么判断的？

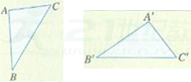
是，通过旋转平移，两个三角形可以完全重合，是全等图形

练习1

一、判断下列说法是否正确

1.全等图形的形状和大小都相同.（√）

2.两个正方形是全等图形.（×）

3.面积相同的两个直角三角形是全等图形.（×）

二、下列各组图形中是全等图形的是（　B　）

讲授新课 ：能够完全重合的两个三角形叫做全等三角形.

两个全等三角形重合时，互相重合的顶点叫对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角.

“全等”可用符号“≌”来表示，如△ABC 和△A’B’C’全等，记作“△ABC ≌△A’B’C’”，读做“三角形ABC全等三角形A’B’C’”.

注意：

用符号“≌”表示两个三角形全等时，通常把对应顶点的字母写在对应位置上。

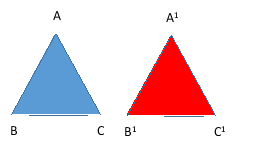如图，△ABC≌△A’B’C’,则：

对应顶点是___A和A’，B和B’，C和C’__

对应边是______BC和B’C’，AB和A’B’，CA和C’A’___

对应角是___∠A和∠A’，∠B和∠B’，∠C和∠C’_____.

寻找对应元素的规律：

1.   有公共边的，公关边是对应边
2.   有公共角的，公关角是对应角
3.   有对顶角的，对顶角是对应角
4.   两个全等三角形的最大边是对应边，最小边是对应边
5.   两个全等三角形的最大角是对应角，最小角是对应角

例题精讲

例1 如图，△AOC与△BOD全等，用符号“≌”表示这两个三角形全等。已知∠A与∠B是对应角，写出其余的对应角和各对对应边。

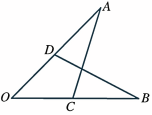
解： △AOC≌△BOD

因为∠A与∠B是对应角，所以其余的对应角是：

∠AOC与∠BOD，∠ACO与∠BDO；

对应边是：OA与OB，OC与OD，AC与BD

想一想：

两个全等三角形的位置变化了，对应顶点会变吗？

对应边、对应角的大小有变化吗？

由此你能得到什么结论？

对应顶点不会变

对应边相等、对应角相等

全等三角形的性质：全等三角形的对应边相等，对应角相等

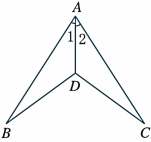
例2 如图，AD平分∠BAC，AB=AC。△ABD与△ACD全等吗？

解： △ABD≌△ACD，BD=CD，∠B=∠C，理由如下：

由AD平分∠BAC，知∠1=∠2,。

因此，将图1沿AD对折时，射线AC与射线AB重合。

∵AB=AC，

∴点C与点B重合，也就是△ACD与△ABD重合（图2）

∴ △ABD≌△ACD

∴BD=CD

∠B=∠C

课堂检测：

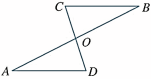
1、如图，△OAD与△OBC 全等，∠A与∠B是对应角． 找出其余的对应角和各对对应边，并用符号表示这两个三角形全等．

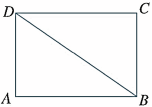
2.如图，BD是长方形ABCD的一条对角线．

(1)△ABD与△CDB全等吗？ 你是怎样知道的？

(2) 如果你认为△ABD与△CDB全等，请用符号表示，并说出它们的对应边和对应角．

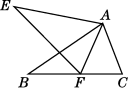
3.如图，△ABC≌△AEF，AB＝AE，∠B＝∠E，则对于结论：①AC＝AF；②∠FAB＝∠EAB；③EF＝BC；④∠EAB＝∠FAC.其中正确的结论有(　　)

A．1个    B．2个   

C．3个    D．4个

答案C

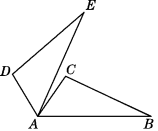
4.如图，已知△ADE≌△ACB，∠EAC＝10°，∠B＝25°，∠BAD＝120°，求∠DAE，∠C的度数．

解：∵∠EAC＝10°，∠BAD＝120°，

∴∠DAE＋∠CAB

＝∠BAD－∠EAC

＝120°－10°＝110°.

∵△ADE≌△ACB，

∴∠DAE＝∠CAB，∴∠DAE＝∠CAB＝55°，

∴∠C＝180°－∠B－∠CAB＝180°－25°－55°＝100°.

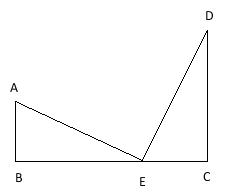
5.如图，Rt△ABE≌Rt△ECD，其中AB的对应边为EC，则以下结论：①AE=DE；②AE⊥DE；③BC=AB+CD；④AB∥CD，其中一定成立的是（　　）

A．①②④   B．②③④   C．①③④    D．①②③④

解：∵Rt△ABE≌Rt△ECD，
∴AE=DE，AB=CE，BE=CD，故①正确，
∠AEB=∠D，
∴BC=CE+BE=AB+CD，故③正确；
∵∠D+∠DEC=90°，
∴∠AEB+∠DEC=90°，
∴∠AED=180°-（∠AEB+∠DEC）=180°-90°=90°，
∴AE⊥DE，故②正确；
又∵∠B=∠D=90°，
∴∠B+∠D=180°，
∴AB∥CD，故④正确，
综上所述，一定成立的有①②③④．
故选D．

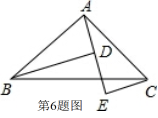
6.   如图，A、D、E三点在同一直线上，且△BAD≌△ACE，试说明：
   （1）BD＝DE＋CE；
   （2）△ABD满足什么条件时，BD∥CE？

21世纪教育网版权

7.

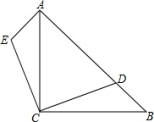
7.如图，在Rt△ABC中，∠ACB＝90°，且AC＝BC＝4cm，已知△BCD≌△ACE．

求四边形AECD的面积．

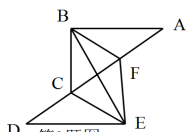
8。如图，已知△ACB≌△DFE  （1）求证：AB∥DE    （2）求证：DC=AF

888888

8

、88 

七、课堂小结，作业布置

小结：1.全等图形的定义

2.全等三角形的定义、表示

3.全等三角形的性质

作业：课本P24页第1、3 题