初中湘教版1.4 角平分线的性质巩固练习

[角平分线的性质]

一、选择题

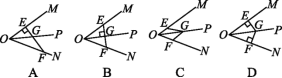
1.OP是∠MON的平分线,点E,F,G分别在射线OM,ON,OP上,则可以解释定理“角平分线上的点到角的两边的距离相等”的图形是              (　　)

2.如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长是 (　　)

A.2 B.3 C.4 D.6

3.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P.小明说:“射线OP就是∠BOA的平分线.”他的依据是              (　　)

A.角的内部到角的两边距离相等的点在角的平分线上

B.角的平分线上的点到角的两边的距离相等

C.三角形三条角平分线的交点到三条边的距离相等

D.以上均不正确

4.如图,已知BD是∠ABC的平分线,DE是BC的垂直平分线,∠BAC=90°,AD=3,则CE的长为 (　　)

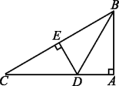
A.6 B.5 C.4 D.3

二、填空题

5.如图,点P在∠AOB的内部,PC⊥OA于点C,PD⊥OB于点D,PC=3 cm,当PD=

　　　　cm时,点P在∠AOB的平分线上. 

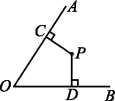
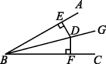
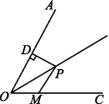
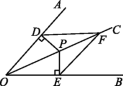
6.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C,若EC=1,则OF=　　　　. 

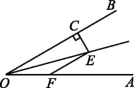
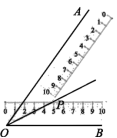
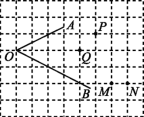
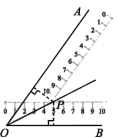
7.在正方形网格中,∠AOB的位置如图所示,则点P,Q,M,N中在∠AOB的平分线上的是点　　　　. 

8.(2020湘潭)如图,P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且PD=3,M是射线OC上一动点,则PM的最小值为　　　　. 

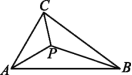
9.如图,在△ABC中,∠CAB和∠CBA的平分线交于点P,连接PC.若△PAB,△PBC,△PAC的面积分别为S1,S2,S3,则S1　　　　S2+S3.(填“>”“<”或“=”) 

三、解答题

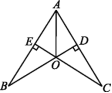
10.如图,已知CE⊥AB于点E,BD⊥AC于点D,BD,CE相交于点O,且AO平分∠BAC.

求证:OB=OC. 

图   

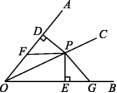
11.如图,已知P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F,G分别是OA,OB上的点,且PF=PG,DF=EG.

求证:OC是∠AOB的平分线. 

12.已知:如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,F是OC上的另一点,连接DF,EF.求证:DF=EF.

图   

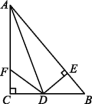
13.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,DB=DF.

求证:(1)CF=EB;

(2)AB=AF+2EB.

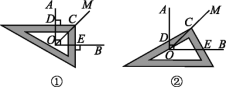
 [归纳猜想] 已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角尺的直角顶点与点C重合,它的两条直角边分别与OA,OB交于点D,E.

(1)如图①,当CD⊥OA于点D,CE⊥OB于点E时,求证:CD=CE.

(2)当三角尺绕点C旋转到CD与OA不垂直时,在图②的情况下,(1)中的结论是否还成立?若成立,请给予证明;若不成立,请写出你的猜想,不需证明.

答案

1.D　2.D

3. A　如图,过两把直尺的交点P作PE⊥OA于点E,PF⊥OB于点F.∵两把长方形直尺完全相同,∴PE=PF,∴OP平分∠AOB(角的内部到角的两边距离相等的点在角的平分线上).

4. D　∵DE是BC的垂直平分线,

∴DB=DC,∴∠C=∠DBC.

∵BD是∠ABC的平分线,DE⊥BC,DA⊥AB,

∴∠ABD=∠DBC,DE=AD=3.

∵∠BAC=90°,

∴∠C=∠DBC=∠ABD=30°,

∴CD=2DE=6,∴CE==3.

5.3　6.2　7.Q

8. 3

 根据垂线段最短,可知当PM⊥OC时,PM最小.当PM⊥OC时,

又∵OP平分∠AOC,PD⊥OA,PD=3,

∴PM=PD=3.故答案为3.

9.<

10.证明:∵CE⊥AB,BD⊥AC,且AO平分∠BAC,

∴OE=OD.

在△BOE和△COD中,

∵∠BEO=∠CDO,OE=OD,∠BOE=∠COD,

∴△BOE≌△COD,∴OB=OC.

11.证明:∵PD⊥OA,PE⊥OB,

∴∠PDF=∠PEG=90°.

在Rt△PFD和Rt△PGE中,

∵PF=PG,DF=EG,

∴Rt△PFD≌Rt△PGE,

∴PD=PE.

∵P是OC上一点,PD⊥OA,PE⊥OB,

∴OC是∠AOB的平分线.

12.证明:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,

∴PD=PE.

在Rt△OPD和Rt△OPE中,

∵OP=OP,PD=PE,

∴Rt△OPD≌Rt△OPE(HL),

∴OD=OE.

∵OC是∠AOB的平分线,

∴∠DOF=∠EOF.

在△ODF和△OEF中,

∵OD=OE,∠DOF=∠EOF,OF=OF,

∴△ODF≌△OEF(SAS),

∴DF=EF.

13.证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,

∴DE=DC.

在Rt△CDF和Rt△EDB中,

∵DC=DE,DF=DB,

∴Rt△CDF≌Rt△EDB(HL),

∴CF=EB.

(2)由(1)知DC=DE,CF=EB.

在Rt△ADC与Rt△ADE中,

∵DC=DE,AD=AD,

∴Rt△ADC≌Rt△ADE(HL),∴AC=AE,

∴AB=AE+EB=AC+EB=AF+CF+EB=AF+2EB.

[素养提升]

解:(1)证明:∵OM是∠AOB的平分线,CD⊥OA于点D,CE⊥OB于点E,∴CD=CE.

(2)(1)中的结论还成立.

证明:如图,过点C分别作CK⊥OA,CH⊥OB,垂足为K,H.

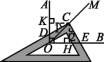
∵OM为∠AOB的平分线,CK⊥OA,CH⊥OB,

∴CK=CH,∠CKD=∠CHE=90°.

∵∠1与∠2都为旋转角,

∴∠1=∠2.

在△CKD与△CHE中,

∵∠CKD=∠CHE,CK=CH,∠1=∠2,

∴△CKD≌△CHE,

∴CD=CE.