初中数学人教版九年级上册22.1.4 二次函数y＝ax2＋bx＋c的图象和性质课后复习题

22.1.4　二次函数y=ax2+bx+c的图象和性质

一、能力提升

1.二次函数y=ax2+x+1的图象必过点(　　)

A.(0,a) B.(-1,-a)

C.(-1,a) D.(0,-a)

2.已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则(　　)

A.y3<y2<y1 B.y3<y1<y2

C.y2<y3<y1 D.y1<y3<y2

3.已知二次函数y=ax2-bx+c(a≠0)的图象经过第一象限的点(1,-b),则一次函数y=bx-ac的图象不经过(　　)

A.第一象限 B.第二象限

C.第三象限 D.第四象限

4.如图,现要在抛物线y=x(4-x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下:

甲:若b=5,则点P的个数为0;

乙:若b=4,则点P的个数为1;

丙:若b=3,则点P的个数为1.

下列判断正确的是(　　)

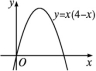
A.乙错,丙对

B.甲和乙都错

C.乙对,丙错

D.甲错,丙对

5.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如下表:

经检查,发现表格中恰好有一组数据计算错误,请你根据上述信息写出该二次函数的解析式:　　　　　　　　　　　. 

6.若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数解析式为　　　　　　　　　　　　　　　. 

7.已知实数x,y满足x2+3x+y-3=0,则x+y的最大值为　　　　　. 

8.已知二次函数y=ax2-5x+c的图象如图所示.

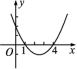
(1)试求该二次函数的解析式和它的图象的顶点坐标;

(2)观察图象回答,何时y的值随x值的增大而增大,何时y的值随x值的增大而减小?

(3)如果将图中抛物线先向左平移3个单位长度,再向下平移4个单位长度,试确定所得到的抛物线的解析式.

★9.如图,四边形ABCD是菱形,点D的坐标是(0,),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点,CE⊥AB于点E.

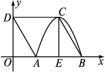
(1)求A,B,C三点的坐标;

(2)求经过A,B,C三点的抛物线的解析式;

(3)若将上述抛物线沿其对称轴向上平移后恰好过点D,求平移后抛物线的解析式,并指出平移了多少个单位长度?

二、创新应用

10.已知二次函数y=x2-2mx(m为常数),当-1≤x≤2时,函数值y的最小值为-2,则m的值是 (　　)

A. B. C. D.-

★11.在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.

(1)求抛物线的顶点坐标.

(2)横、纵坐标都是整数的点叫做整点.

①当m=1时,求线段AB上整点的个数;

②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.

一、能力提升

1.C　2.B　3.C　4.C

5.y=x2-4x+3　由于表格中只有一组数据计算错误,根据抛物线的轴对称性及图象经过点(0,3),(4,3)可得抛物线的对称轴为直线x=2,而根据图象经过点(1,0),(3,0)亦可得抛物线的对称轴为直线x=2,所以抛物线的对称轴可确定为直线x=2,而且能断定这四组数据都不会错.所以从这四个点中任意选3个可求得其解析式.如设二次函数解析式为y=a(x-1)(x-3),把x=0,y=3代入得3=a(0-1)·(0-3),解得a=1,所以y=(x-1)(x-3)=x2-4x+3.

6.y=-x2+4x-3　设抛物线的解析式为y=a(x-2)2+1,将B(1,0)代入y=a(x-2)2+1,得a=-1.

因此抛物线的函数解析式为y=-(x-2)2+1,展开得y=-x2+4x-3.

7.4　易知y=-x2-3x+3,则x+y=-x2-2x+3=-(x+1)2+4,

所以x+y的最大值为4.

8.解(1)由图象知,抛物线过点(1,0),(4,0),将坐标代入函数解析式,得

解得

故所求二次函数的解析式为y=x2-5x+4.

又因为y=x2-5x+4=x-2-,所以函数图象的顶点坐标为.

(2)由(1)知,a=1>0,抛物线的对称轴为直线x=,从图象知,当x>时,y随x值的增大而增大;当x<时,y随x值的增大而减小.

(3)由(1)知,y=x2-5x+4=,将抛物线先向左平移3个单位长度,再向下平移4个单位长度,则所得抛物线的解析式为y=-4,

即y=x2+x-6.

9.解(1)由抛物线的对称性可知AE=BE.

在Rt△AOD和Rt△BEC中,

∵OD=EC,AD=BC,

∴Rt△AOD≌Rt△BEC(HL).

∴OA=EB=EA.

设菱形的边长为2m,

在Rt△AOD中,m2+()2=(2m)2,解得m=1.

∴DC=2,OA=1,OB=3.

故A,B,C三点的坐标分别为(1,0),(3,0),(2,).

(2)设抛物线的解析式为y=a(x-2)2+,代入点A的坐标(1,0),得a=-,

所以抛物线的解析式为y=-(x-2)2+.

(3)设平移后抛物线的解析式为y=-(x-2)2+k,代入点D的坐标(0,),得k=5,

所以平移后的抛物线的解析式为y=-(x-2)2+5.所以平移了5=4个单位长度.

二、创新应用

10.D　y=x2-2mx=(x-m)2-m2,

①若m<-1,则当x=-1时,y=1+2m=-2,解得m=-;

②若m>2,则当x=2时,y=4-4m=-2,解得m=<2(舍);

③若-1≤m≤2,则当x=m时,y=-m2=-2,

解得m=或m=-<-1(舍),综上可知,m的值为-.故选D.

11.解(1)∵y=mx2-2mx+m-1=m(x-1)2-1,

∴抛物线的顶点坐标为(1,-1).

(2)①∵m=1,

∴抛物线对应的解析式为y=x2-2x.

令y=0,得x=0或x=2,不妨设A(0,0),B(2,0),则线段AB上整点的个数为3.

②如图所示,抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,则点A在(-1,0)与(-2,0)之间(包括点(-1,0),不包括点(-2,0)),当抛物线经过点(-1,0)时,m=;

当抛物线经过点(-2,0)时,m=;

故m的取值范围为<m≤.