北师大版（2019）高中数学 选择性必修第二册 第二章导数及其应用数列A卷基础夯实（Word含答案解析）

第二章 导数及其应用 数列 A卷 基础夯实-2021-2022学年高二数学北师大版（2019）选择性必修二单元测试AB卷

【满分：100分】

一、选择题：本题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1.若，则(   )

A.1 B.2 C.4 D.8

2.已知函数在点处的切线的倾斜角是，则的值为(   )

A. B. C. D.1

3.一个物体的位移s(米)与时间t(秒)的关系为，则该物体在4秒末的瞬时速度是(   )

A.2米/秒 B.3米/秒 C.4米/秒 D.5米/秒

4.曲线在处的切线与坐标轴所围成的三角形的面积为(   )

A. B. C. D.

5.关于函数的极值，下列说法正确的是（    ）

A.导数为零的点一定是函数的极值点

B.函数的极小值一定小于它的极大值

C.一个函数在它的定义域内最多只有一个极大值和一个极小值

D.若一个函数在某个区间内有极值，则这个函数在该区间内不是单调函数

6.已知函数(e为自然对数的底数)，若在区间上有两个不相等的实数根，则m的取值范围为(   )

A. B. C. D.

7.已知函数，在处的切线方程为(   )

A.  B.

C. D.

8.经过点作曲线的切线有(   )

A.1条 B.2条 C.3条 D.4条

9.若函数有两个极值点，则实数a的取值范围是(   )

A. B. C. D.

10.下列导数运算正确的是(   )

A. B. C. D.

二、填空题：本题共5小题，每小题5分，共25分.

11.已知函数的极小值为a，则a的值为_________.

12.已知曲线在处的切线方程为，则_______.

13.函数的极小值是         .

14.已知函数，曲线在点处的切线方程是______.

15.若函数的图象在点处切线的斜率为，则___________.

三、解答题：本题共2小题，共25分.解答应写出文字说明、证明过程或演算步骤.

16. （10分）设函数的导函数为，若函数的图象关于直线对称，且.

（1）求实数a，b的值；

（2）求函数的极值.

17. （15分）求下列函数的极值：

（1）；

（2）.

答案以及解析

1.答案：A

解析：由题意，所以，所以.故选：A.

2.答案：A

解析：由题意知.

3.答案：A

解析：因为，所以，因为当时，.所以该物体在4秒末的瞬时速度是2米/秒.

4.答案：A

解析：由题意得，，则，所以曲线在处的切线的斜率，且切点坐标为，所以曲线在处的切线方程为，令，则；令，则，则切线与坐标轴所围成的三角形的面积为，故选A.

5.答案：D

解析：对于A选项，取，则，，当时，，

故不是函数的极值点，故A不正确；

极值是函数的局部性质，极大值与极小值之间一般来说没有大小关系，故B不正确；

一个函数在它的定义域内可能有多个极大值和极小值，故C不正确；

若一个函数在某个区间内有极值，则这个函数在该区间内不是单调函数，D正确.

故选：D.

6.答案：C

解析：因为，记，则.

当时，，所以函数在上单调递减.

又，所以当时，，单调递增；

当时，，单调递减.

当时，有极大值也是最大值，.

若在上有两解，应有，，

所以，此时，所以在上有两解成立，故选C.

7.答案：A

解析：由题可知，，所以函数在处的切线斜率，所以切线方程为，即，故选A.

8.答案：C

解析：因为，所以曲线在点处的切线方程为.将代入，得.因为，所以方程有两个不同的根，且根不为0，所以方程共有3个不问的根，即经过点作曲线的切线有3条.

9.答案：D

解析：，因为有两个极值点，所以函数在上有两个不相等的零点，由解得.

10.答案：C

解析：，故A错误；，故B错误；令，，因为，，所以，故C正确；，故D错误.

11.答案：e

解析：由题，，若，则当时，，单调递增，此时不存在极值，不符合题意，所以，易知在上单调递增，且当时，，当时，，所以存在唯一的，使得.当时，，单调递减；当时，，单调递增.所以的极小值，因为，所以，即，设，因为，所以在上单调递减，又1，所以，从而.

12.答案：e

解析：，，由，得.则，，把代入切线方程，得，，故答案为：e.

13.答案：-856

解析：，

，令，解得：或，

令，解得：，

故函数在递增，在递减，在递增，

故函数的极小值是，故答案为：-856.

14.答案：

解析：由，得，，又，∴曲线在点处的切线方程是，
即
故答案为：
 

15.答案：

解析： ，

,

函数的图象在点处切线的斜率为-1，

,解得：，

.

故答案为：

16.答案：（1）因为，

所以，

从而，

即的图象关于直线对称，

则，即.

又，即，所以.

（2）由（1），知，

.

令，解得或.

当时，，即在上单调递增；

当时，，即在上单调递减；

当时，，即在上单调递增.

从而函数在处取得极大值，为，在处取得极小值，为.

解析：

17.答案：（1）.

令，解得，.

当x变化时，，的变化情况如下表：

由上表看出，当时，取得极小值，为；

当时，取得极大值，为.

（2）.

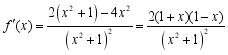令，解得，.

当x变化时，，的变化情况如下表：

由上表看出，当时，取得极小值，为；

当时，取得极大值，为.