高中人教A版 (2019)4.1 指数一等奖教案设计

第4课时  指数函数的图象和性质

（一）教学内容

指数函数的概念.

（二）教学目标

1、通过描点法或信息技术画出具体指数函数的图象，能探索并理解指数函数的单调性与特殊点，发展数学抽象素养.

2、通过指数函数概念、图象与性质的研究，能进一步体会研究具体函数的一般思路和方法，提升数学抽象、直观想象素养.

（三）教学重点与难点

教学重点：指数函数的图象和性质.

教学难点：用“增长率”刻画变化规律，以及指数函数单调性的抽象概括.

（四）教学过程设计

引导语：今天我们类比研究幂函数性质的过程和方法，进一步研究指数函数.

问题1：研究一类新函数的思路和方法？

师生活动：学生通过回忆研究幂函数的过程和方法得出结论，教师板书：

思路：定义、表示——图象与性质——应用

研究一类具体函数的基本过程：

①根据函数解析式求出函数的定义域；

②画出函数的图象；

③利用图象和解析式，讨论函数的值域、单调性、奇偶性等.

设计意图: 通过回顾已有经验，引导学生体会研究一类函数的方法，给出研究一类函数的一般内容、基本思路和方法，发展学生的数学抽象核心素养.

问题2：如何用描点法画出函数的图象？

师生活动：（1）学生思考后回答：通过解析式，可以得到函数的定义域，并可以知道函数既不是奇函数也不是偶函数.

（2）用excel列表

（3）描点，连线（可用geogebra完成这三个步骤）

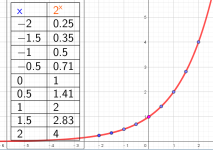
设计意图: 让学生先观察函数解析式的特点，对函数的定义域、单调性、奇偶性等进行初步判断，这样可以使学生提高取点的目的性，使图象更好地反映函数的特征，而且可以使学生体会高中阶段研究函数性质的新特点，发展学生的数学抽象核心素养.

问题3：画出函数的图象，并与函数的图象进行比较，它们有什么关系？能否利用函数的图象，画出函数的图象？

师生活动：（1）学生思考后动手画图，教师用geogebra画出函数和的图象.观察图象容易得出图象关于y轴对称.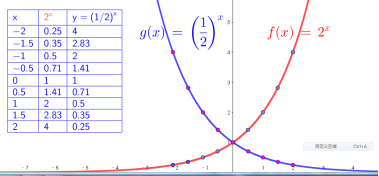

（2）追问: 为什么函数和的图象关于y轴对称？函数的图象有什么关系？

（3）学生讨论后教师指出：因为，点（x,y）与点（-x,y）关于y轴对称，所以函数图象上任意一点P（x,y）关于y轴的得出点P1（-x,y）都在函数的图象上，反之亦然.由此可知，底数互为倒数的两个指数函数的图象关于y轴对称.

设计意图: 让学生先观察函数图象，得出，并进行证明，发展学生的直观想象、逻辑推理和数学抽象核心素养.

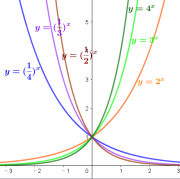
问题4：选取底数的若干个不同的值，在同一直角坐标系内画出相应的指数函数的图象.观察这些图象的位置、公共点和变化趋势，它们有哪些共性？由此你能概括出指数函数=的值域和性质吗？

师生活动：（1）教师用geogebra画出底数的指数函数图象.

追问①：观察这些图象的位置、公共点和变化趋势，它们有哪些共性？由此你能概括出指数函数的定义域、值域和单调性吗？

追问②：当时，指数函数的图象位置、公共点、变化趋势、定义域、值域和单调性如何？当时，指数函数的情况又如何呢？

追问③：比较与指数函数的图象和性质，看它们有什么区别与联系？

（2）将探索的结果填入下表：

教师提出问题，引导学生根据图象进行探索、思考，逐步抽象出指数函数的图象特征和性质.为了画更多的函数图象，帮助进行观察、归纳，可以利用信息技术工具.由此逐渐引导学生对指数函数进行分类，得到它的单调性和特殊点的规律.

设计意图：通过信息技术工具画出函数图象，比较不同指数函数的图象，归纳出它们的共同特征，抽象出指数函数的性质，发展学生的直观想象和数学抽象核心素养.

问题5：能否利用函数的单调性比较两个数的大小？

师生活动：例3 比较下列各题中两个值的大小：

（1）    （2）  （3）

教师引导学生将每一组中的两个值可以看作一个指数函数的两个函数值，从而利用指数函数的单调性进行比较.对于（1）（2），可以直接利用指数函数的单调性比较；对于（3），不能看作某一个指数函数的两个函数值.可以利用函数的单调性，以及“”这条性质把他们联系起来.

设计意图：通过应用函数的单调性比较大小，进一步理解指数函数的单调性，发展学生的逻辑推理核心素养.

例4：如右图，某城市人口呈指数增长.

（1）根据图象，估计该城市人口每翻一番所需的时间（倍增期）；

（2）该城市人口从80万人开始，经过20年会增长到底数万人？

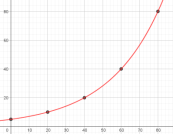
师生活动：教师引导学生学生对问题进行分析，根据该城市人口呈指数增长，而同一指数函数的倍增期是相同的，所以可以从图象中选取适当的点计算倍增期.要计算20年后的人口数，关键是要找到20年与倍增期的数量关系，由于倍增期是20年，因此容易得到“从80万人开始，20年后人口大约会增长到160万人”.

设计意图：通过应用函数图象解决问题，进一步认识指数函数的图象，并由图象理解指数函数的概念和性质.

问题6：通过本节课的学习，你对研究函数的内容和方法有什么更进一步的认识？对比以前学习过的一些具体函数，你能建立指数函数和它们的联系吗？

师生活动：教师引导学生回顾本节课学习的主要内容，并完成下表：

设计意图：建立指数函数与学习过的其它函数的联系，进一步体会研究体会研究具体函数的内容、过程和方法，通过该问题教师与学生一起回顾本单元学习的指数函数的概念、图象和性质.

（五）目标检测设计

1、课堂检测

教材第118页练习1,2,3

设计意图：1题考查指数函数的图象，2题考查学生指数函数的单调性在比较大小中的应用，3题应用图象描述实际问题的变化规律，进一步认识指数函数的图象，理解指数函数的概念和性质.

2、课后作业

教材第118页习题4.2   1,2,3,4,5,6

设计意图：1题考查函数的定义域，2题4题考查指数增长模型，3题6题考查指数函数单调性的应用，5题考查学生对指数函数的图象和性质的掌握.

（六）课后反思